|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Strauss W.A. Ч Partial Differential Equations: An Introduction |
|
|
 |
| ѕредметный указатель |
Fourier series, pointwise convergence 125 132 140
Fourier series, triple 250 261
Fourier series, uniform convergence 124 135Ч136
Fourier sine series 84
Fourier sine series, and boundary conditions 111
Fourier sine series, coefficients in 101
Fourier sine series, double 158
Fourier transform 325Ч329
Fourier transform, convolution 328
Fourier transform, in spherical coordinates 332 357
Fourier transform, in three dimensions 329
Fourier transform, properties 327
FourierТs law of heat 16 24
Fredholm alternative 301
frequency 85 256
Frequency variable 326
Full Fourier series 103Ч107
Full Fourier series, complex form 112Ч113
Function of two variables 3
fundamental frequency 85 256
Fundamental solution 48
future 231
Gamma function 268 338 395Ч396
Gas dynamics 22 25 343Ч345
Gauge, group 356
Gauge, invariance 356
Gauge, theory 355Ч356
Gauss Ч Seidel method 210
Gaussian and diffusion equation 48
Gaussian, transform of 326
GaussТs theorem 393
Gelfand Ч Levitan method 371
General Fourier series 114 248
General solution 32
Geometric method 6 9 359
Ghost points 198
GibbТs phenomenon 136Ч138
Grad,  169 169
Gradient 386
Gram Ч Schmidt orthogonalization 119 247
Graph of a function 392
Graphing method 92Ч95
Green 169
GreenТs first identity 120 171
GreenТs function 48 178Ч179
GreenТs function, revisited 320Ч324
GreenТs function, symmetry 179Ч181
GreenТs second identity 115 176 246
GreenТs Theorem 392
GreenТs theorem, method using 73Ч74
Ground state 173 243 285
Guitar 11 265
Half-line 55Ч61
Half-space 181Ч183
Hammer blow 37 108Ч109
Hankel function 271 348
Harmonic function 16
Harmonic function, half-ball 187
Harmonic function, half-space 181Ч183
Harmonic function, infinitely differentiable 163
Harmonic function, maximum principle 162Ч163 172
Harmonic function, mean value property 162 171Ч172
Harmonic function, minimum energy 173Ч174 374
Harmonic function, PoissonТs formula 159Ч162
Harmonic function, quadrant 188
Harmonic function, rectangle 155Ч157
Harmonic function, representation formula 176Ч178
Harmonic function, rotationally invariant 151 153
Harmonic function, sphere 183Ч186
Harmonic oscillator, quantum mechanical 239Ч240
Heap of water 367
Heat conductivity 16
Heat equation 16
Heat exchange 18
Heat flow 15Ч16 19 22 65 298
Heat flow, convection 52
Heat flow, energy absorption 97
Heat flow, maximum principle 41
Heat flow, Robin condition 90
Heat flow, source function 49. 236 330Ч331
Heat flux 16 25
Heaviside function 318 326
Heisenberg uncertainty principle 327Ч328
Helium ion 17
Hermite polynomial 240
HermiteТs differential equation 239
Homogeneous linear equation 2 5
HookeТslaw 21
Hopf maximum principle 172
Hot Spot 41 49
Hotrod 97
HuygensТs principle 39Ч40 222 227
Hydrogen atom 17Ч18 241Ч244 280Ч282 298
Hydrogen atom, continuous spectrum 351
Hyperbolic equation 28 30 53
Hyperbolic equation, Klein Ч Gordon equation 353 356
IC see УInitial condition
Ill-conditioned matrix 26
Ill-posed problem 26
Impedance 23
Implicit function theorem 392
Implicit scheme 198
Incident wave 346
Incoming wave 346
Indicial equation 394
Infinite series 121Ч123 388Ч389
Infinitely differentiable solution 79 139 163
Inhomogeneous elliptic equation 301
Inhomogeneous linear equation 2 5 12 15
Inhomogeneous linear equation on finite interval 142
Inhomogeneous linear equation on half line 67 76
Inhomogeneous linear equation on whole line 65 69
Inhomogeneous medium 297 347 374
Inhomogeneous string 346Ч347
Initial condition 20 (see also УBoundary condition)
Inner product 114 116Ч117 246 255 298
Instability of matrix 26
Instability, diffusion equation 53
Insulation 22 88 90
Integral of derivatives 392Ч393
Intermediate Value Theorem 385
Invariance, diffusion equation 45Ч46
Invariance, KdV equation 374
Invariance, under dilations 40 46
Invariance, under Lorentz tranformations 221Ч222
Invariance, under rotations 150Ч153
Invariance, wave equation 40
Inverse scattering 369Ч372
Inversion formula, Fourier transform 326
Inversion formula, Laplace transform 335
Irrotational flow 23 147 345
Isotropic 150
Jacobi iteration 209Ч210
Jacobian 4 387
Jump conditions 24
Jump discontinuity 80 124 364 385
Kadomstev Ч Petviashvili equation 372
kinetic energy 38 218
Kinetic theory of gases 378
Kirchhoffs formula 222
Klein Ч Gordon equation 222 353Ч354
Klein Ч Gordon equation, solution of 356Ч357
Korteweg Ч deVries (KdV) equation 367
Kruskal, M. 368
Lagrange multiplier 284
LaguerreТs differential equation 242 281
Laplace equation 2 16 146
Laplace equation, annulus 165Ч166 299
Laplace equation, circle 159Ч162
Laplace equation, computation 208Ч210
| Laplace equation, cube 157Ч158
Laplace equation, exterior of a circle 166 Ч167
Laplace equation, half-plane 187 332
Laplace equation, half-space 181Ч183
Laplace equation, maximum principle 148
Laplace equation, rectangle 155Ч156
Laplace equation, sphere 183Ч186
Laplace equation, wedge 164Ч165
Laplace transform 334
Laplace transform, techniques 334Ч337
Laplacian 14
Laplacian, four-dimensional 188
Laplacian, GreenТs function 178 320
Laplacian, invariance 150Ч153
Laplacian, Neumann function 188
Laplacian, polar coordinates 151
Laplacian, spherical coordinates 153
Legendre function 274Ч278
Legendre function, associated 260 278
Legendre function, generating function 277
Legendre function, Legendre polynomial 118 275
Legendre function, normalizing constants 275
Legendre function, RodriguesТ formula 276
Legendre function, zeros 276
LegendreТs differential equation 259Ч260 274
LegendreТs differential equation, associated 277
Light 22
Light cone 216Ч217
Light ray 230
LIMIT 384
Limit from the right, left 384
Linear elements 214
Linear operator 2
Linearity 2
Linearized Equation 22 345 380
Linearly dependent 5
Lorentz transformation 221
magnetic quantum number 279
Marching in time 192
Matrix equation 26
Maximin principle 307
Maximum of a function 385
Maximum principle, diffusion equation 41
Maximum principle, Hopf form 168 172
Maximum principle, Laplace equation 148 162
MaxwellТs equations 22 39 339Ч342
Mean value property 162 171Ч172
Mean value property, discrete 209
Mean-square convergence 122 124 249 295
Mesh size 189
Mesons 353
Metric, 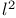 127 127
Minimal surface equation 377
Minimax principle 291 294
Minimum principle, diffusion equation 41
Minimum principle, for first eigenvalue 284
Minimum principle, for nth eigenvalue 286
Minimum principle, Laplace equation 148
Minimum problem 284 374
Molecules 18
Momentum, conservation of 343 368
Momentum, density 40
Momentum, variable 327
Multiplicity 247Ч248 266
musical notes 85
N-soliton 372
Neumann condition 20 293Ч294 307
Neumann condition, DirichletТs principle 175
Neumann condition, discretization 197Ч198
Neumann condition, trial function 294
Neumann function for a domain 188
Neumann function for BesselТs equation 271
Neumann problem, finite interval 87 112
Neumann problem, half-line 57
Neumann problem, uniqueness 174
Neumann problem, wedge 164
NewtonТs Law of Cooling 18 22
Nodal set 264Ч268 313
nodes 243 264
Nonexistence 25
Nonlinear interaction 2 368
Nonlinear wave equation 2 205
Nonuniqueness 25
Norm,  126 126
Norm, uniform 70
Normal derivative 20
Normal mode 86
Normal vector 13 20 217
Normal velocity 23
Normalizing constants 131 270 275 370
Nth term test for divergence 388
Null vector 231
Observable 18
Odd extension 56 111 114
Odd function 55 110
ODE 1
ODE, arbitrary constants 3
ODE, Bessel 252 268
ODE, Euler 160 394
ODE, existence theorem 393
ODE, Hermite 239
ODE, Laguerre 242 281
ODE, method of power series 239 242 253 274 394
ODE, singular point 393
One-sided limit 124Ч125 384
Open interval 384
Open set 148 386
Open window, BC at 23
Operator 2 18
Operator, method 66 74 233
Orbital quantum number 279
Order 1
Orthogonal 114 116 117 247
Outgoing wave 348
Overdetermined 25 26
Overtone 85
Parabolic PDE 28 30
Parametrization of surface 391
ParsevalТs equality 128 327
Partial sum 388
Particles, elementary 353
Past history 38 69 221 231
Pauli matrices 354
Perfect thermal conduction 22
Period 61 109
periodic extension 109
Periodic function 109 125
Periodic traveling wave 373
Phase plane 381
Phase shift 372
Piecewise  391 391
Piecewise continuous 124 385
Pitchfork 380
PlancherelТs theorem 327
PlanckТs constant 17
Plane wave 221 347 351
plasma 368
Plucked string 35Ч36
Point mass 314
Point spectrum 351
Pointwise convergence 121 125 132 388
Poisson summation formula 330
PoissonТs equation 146 181 320
PoissonТs equation, finite element method 212
PoissonТs formula 159Ч162
PoissonТs formula in three dimensions 185Ч186
Polar coordinates 150 159
Population dynamics 15
Potential continuous spectrum 350Ч351
Potential electric 147 175
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте