|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lukes J., Maly J., Zajicek L. — Fine Topology Methods in Real Analysis and Potential Theory |
|
|
 |
| Предметный указатель |
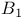 -extension theorem 112 263 266 311 -extension theorem 112 263 266 311
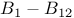 differentiation bases 163—167 differentiation bases 163—167
 -insertion property 22 57 58 62 64 66 117 135 143 145 157 179 190 237 249 253 -insertion property 22 57 58 62 64 66 117 135 143 145 157 179 190 237 249 253
 -measurable function 55 -measurable function 55
 -space 424 430—433 -space 424 430—433
 -bounded 348 -bounded 348
 -harmonic space 328 330 331 346 347 360—364 383 396 412 -harmonic space 328 330 331 346 347 360—364 383 396 412
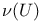 -topology 380 382 383 412 424 428 429 -topology 380 382 383 412 424 428 429
 -approximately continuous function 270 271 283 285 286 -approximately continuous function 270 271 283 285 286
 -derivative 283 -derivative 283
 -lower Lebesgue bounded function 284 -lower Lebesgue bounded function 284
 -regular sequence of intervals 283 -regular sequence of intervals 283
 -superdensity topology 192 193 197 270 -superdensity topology 192 193 197 270
 -topological space 91 94 119 120 247 -topological space 91 94 119 120 247
 -topology 90 94 119 120 247 342 411 -topology 90 94 119 120 247 342 411
(Ba l)-condition 119 180 183 184 293
(bFL)-condition 42
(tFL)-condition 47
a-modification 231—239 270
a-topology 231—239 270
a.e.-modification 230—239 249
a.e.-topology 230—239 249
Absorbent set 359
Abstract category density topology 213 218 221 253
Abstract density topology 212 213—222 224—226 250—254
Abstract in-between theorem 71—75 77—81 95 116 128 280
Ambivalent function 65
Ambivalent set 65 240
Angle differentiation basis 166 179 180 293
Approximate continuity 1 45 63 75 122 149 150 152 157 200 237 260—276 285 320
Averaging principle 318
Axiom of  -lower semicontinuous regularization 329 408 429 -lower semicontinuous regularization 329 408 429
Axiom of broken ellipticity 363
Axiom of upper directed sets 329 408 429
Axiom, domination = D 360 362 381 421
b-closed set 5
b-topology 5
Baire one function 54—69 73—78
Baire property 171
Baire space 86 222 136—140 192 236
Balayage 222 253
Balayaged measure 351 352
Band 361
Base of a set 333 352
Base operator 5 333
Base operator, compatible with measure 196 204 208 253 277
Base operator, essential 21
Base operator, fine 28
Base operator, ideal 22
Base operator, idempotent 8
Base operator, strong 8
Base operator, z-admissible 22
Base operator, z-ideal 22
Bauer’s minimum principle 355 387 417
Berg’s theorem 344 345
Binormality 85 25
Bitopological boundary 389
Bitopological space 85 92 93
Bliedtner — Hansen lemma (=Prop. 11.7) 352 354 426
Blumberg space 240 141 142 151 236 237 246 364
Boundary bitopological 389
Boundary function 255 287 288 291 292 301 309 310 313
Boundary topology 255 257 301 307 311 313 317
Bounded lower  348 348
Brelot property 362
Capacity 408 415 421
Categorial lifting 226 228
Choquet boundary 387
Choquet’s lemma 338
Closure operation 7
Cometrizable topology 133 135 188 247 343
Complete Lusin — Menchoff property of base 103 104 105 108 196—199 201 202 233 275
Complete Lusin — Menchoff property of topology 86 88 90 93 98 109 113 114 118 129 151 192 196—199 201 202 233 237 252 255 25B 267 311 343 363
Condition, (*) 22
Condition, (Ba 1) 179 180 183 184 293
Condition, (bFL) 49—54
Condition, (tFL) 47 49—54
Condition, (W) 289 291 293 294 295 298 306 310
Condition, countable chain = (CCC) 19 182
Condition, essential radius 66 67 183 294
Condition, r-basis (B) 241 244 275
Condition, strong essential radius 67 293
Condition, Tietze’s 92 95
Condition, Urysohn’s 91 101
Cone, standard H-= 329 330 332 344 353 354 360 377
Contingent topology 98 258 259 311 312
Convergence theorem 336
Countable chain condition (CCC) 19 182
Crosswise topology 7 40 45 67 68 137 138
Cube differentiation basis 165 179 180 186 198
de Possel differentiation basis 206 214
Denjoy — Stepanoff theorem 171 172 218
Density point 148 152 164 208
Density theorem 148 164 168 172 173 208
Density topology 1 88 92 93 146 148 151 156 158 160 161 237 261 273
Density topology, determined by a differentiation basis  163—189 198 205 228 244 273 275 276 163—189 198 205 228 244 273 275 276
Density topology, determined by a filter differentiation basis  204 205 208 210 215 204 205 208 210 215
Density topology, determined by a lower density 208 209
Derivative, approximate 272 297 299
Derivative, preponderant 297 298
Derivative, qualitative 300
Differentiation basis 162 179 180 198 205 244
Differentiation basis, angle 166 179 180 293
Differentiation basis, cube 162 179 180 186 198
Differentiation basis, de Possel 206 214
Differentiation basis, filter 201 215 216 226
Differentiation basis, ideal 166 179 180
Differentiation basis, incomplete symmetric 167 179 180 185 187 198
Differentiation basis, interval 165 179 180 198 201 275
Differentiation basis, Morse 207 213 247
Differentiation basis, net 167 179 180 206
Differentiation basis, of Morse type 165 179 180 198
Differentiation basis, rectangle 165 179 180 201
Differentiation basis, right density 166 179 180 184
Differentiation basis, superdensity 166 179 180 192
Differentiation basis, symmetric 164 179 180 186 193 198 201 276
Dirichlet problem 2 327 355 356 430
Dirichlet problem, fine 402
Dirichlet problem, incomplete fine 400
Dispersion point 152 170 181
Domination axiom D 360 362 381 421
Eilenberg — Saks theorem 267 269
Elliptic space 359 360
Essential base operator 31
Essential radius condition 66 67 183 294
Evanescent family 408 409 415 420 422
Evans function 348 349
E’(U) - bounded function 431 432
Filter differentiation basis 203 215 216 226
Fine base operator 38
Fine boundary topology 255 257 301 307 311 313
Fine Dirichlet problem 402
Fine exhaustion 404
Fine sheaf property 381
Fine superfunction 390 391 394
Fine topology 38 43
Fine topology in potential theory 3 318 321 325 332 341 343 345 358 360—364 382
Finely classical solution 394
Finely harmonic function 367 379 398
Finely hyperharmonic function 367 368 370—375 379 380 383 385 389 396 411 413 414 416 420 421
Finely Keldych set 405 406
Finely regular set 336 337 400 404 406 426
Finely resolutive function 390 391 393 422
Finely superharmonic function 367
Function,  -measurable 55 -measurable 55
Function, 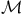 -measurable 57 -measurable 57
Function,  -approximately continuous 270 271 283 285 286 -approximately continuous 270 271 283 285 286
Function,  -lower Lebesgue bounded 284 -lower Lebesgue bounded 284
Function,  -Lipschitzian at x 242 -Lipschitzian at x 242
Function, ambivalent 65
| Function, approximately continuous 1 45 63 75 122 149 150 152 157 200 237 260—276 285 320
Function, approximately differentiable 245
Function, B-finely harmonic 424 426 427 431
Function, B-finely hyperharmonic 424 426 427 428 430 431
Function, Baire one 54—69 73—78
Function, boundary 255 287 288 291 292 301 309 310 313
Function, E(U)-lower bounded 422 416
Function, Evans 348 349
Function, E’(U)-bounded 431 432
Function, finely harmonic 367 379 398
Function, finely hyperharmonic 367 368 370—375 379 380 383 385 389 396 411 413 414 416 420 421
Function, finely hyperharmonic in Fuglede s sense 367
Function, finely resolutive 390 391 393 422
Function, finely superharmonic 367
Function, fundamental caloric 322
Function, fundamental harmonic 317
Function, harmonic 318 327 348 350 351
Function, honorary Baire two 58 59 68 310 312
Function, hyperharmonic 324 328 348 349 355 368 370
Function, Kopcke 260—262
Function, lower 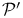 -bounded 424 430 -bounded 424 430
Function, lower  -bounded 348 -bounded 348
Function, lower Lebesgue bounded 263 264 274
Function, pointwise finely hyperharmonic 367 369 373 374 386 413 414
Function, Pompeiu 2 260
Function, quasi-continuous 408 412
Function, quasi-l.s.c. 408—416
Function, separately continuous 58 138 306 311
Function, strongly approximately continuous 165 200 271 276 307 308
Function, super-mean-valued 319
Function, superharmonic 3 324 325 328 350
Function, u-continuous 329
Function, U-quasi-t-continuous 431
Function, universally continuous 329 350
Function, upper Lebesgue bounded 263
Function, weakly  -approximately continuous 2§2 284 286 -approximately continuous 2§2 284 286
Fundamental caloric function 322
Fundamental harmonic function 317
Generator 334 339 351
H-cone, standard = 329 330 332 344 353 354 360 377 424 428
Harmonic function 318 327 348 350 351
Harmonic measure 355
Harmonic space 328 330 331 347 412
Hausdorff — Kempisty method 115 127 132
Honorary Baire two function 58 59 68 310 312
Hyperharmonic function 324 328 348 349 355 368 370
Ideal base operator 72
Ideal differentiation basis 166 179 180
Ideal topology 22 50 138 141 218 251 253
Idempotent base operator 8
Incomplete fine Dirichlet problem 400
Incomplete symmetric differentiation basis 167 179 180 185 187 198
Increasing family 329
Increasingly dense set 330
Insertion property 57 140
Interval differentiation basis 165 179 180 198 201 275
Irregular point 397 398 406
Jarnik — Blumberg method 287 296 300
Keldych operator 405 406
Keldych set 403
Keldych theorem 406
Key lemma 334 340
Kopcke function 260—262
Kuratowski closure operator 8
L-cone 70—72 119
Lebesgue point 263
Lebesgue spine 323
Lifting 223—229 254
Lifting topology 223 224—228 251 253
Lifting, categorial 226 228
Lifting, on 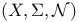 226—229 226—229
Lifting, strong 254
Lower 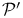 -bounded 424 430 -bounded 424 430
Lower  -bounded 348 -bounded 348
Lower density 207 217 220 223 226 251
Lower Lebesgue bounded function 263 264 274
Lower semicontinuous regularization 408 332 376
Lusin — Menchoff property of  -topology 100 247 342 -topology 100 247 342
Lusin — Menchoff property of base 103_—106 196—199 201 233 240
Lusin — Menchoff property of topology 85 89 90 98 99 101 116 117 120 121 125 126 133 134 196—199 201 233 245 247 248 257 271 343
M-modification 107 110 113 268
M-property 137 138
Measurable cover 163
Measurable kernel 162
Measure sweeping property 353 429
Measure, balayaged 351 352
Measure, harmonic 355
Minimum principle 430
Minimum principle, Bauer’s 355 387
Minimum principle, quasi 421
Modification,  -= 31 -= 31
Modification, a-= 231—239 270
Modification, a.e.-= 230—239 249
Modification, M-= 107 LL0 113 268
Modification, principal = 427
Modification, r-= 240—249
natural order 329 377
Natural topology 380 424
Net differentiation basis 167 179 180 206
Newtonian potential 311 320 322 325 350
Ordinary density topology 51 167 181 188 189 237 239 245—247
Perfect Lusin — Menchoff property 96 97 117
Perfectly binormal space 95 96 119
Perron method 355
Perron solution 3 356 396 401 430
Perron upper solution 388
Point, dispersion 152 170 181
Point, irregular 397 398 406
Point, Lebesgue 263
Point, of density 148 152 164 208
Point, regular 3 393 397 399
Point, semiregular 397 398
Pointwise finely hyperharmonic function 367 369 373 374 386 413 414
Polar set 339 340 361 431
Potential 328 348 349 350 393
Potential, heat 222
Potential, logarithmic 323 325
Potential, Newtonian 317 320 322 325 350
Potential, strict 250 393
Preponderant derivative 297 298
Principal modification 427
Principal operator 427
Principal solution 405
Property,  insertion 22 57 58 62 64 66 117 135 143 145 157 179 190 237 249 253 343 insertion 22 57 58 62 64 66 117 135 143 145 157 179 190 237 249 253 343
Property, (K) 20
Property, Baire 171
Property, complete Lusin — Menchoff of base 103 104 105 108 196—199 201 202 233 275
Property, complete Lusin — Menchoff of topology 86 88 90 93 98 109 113 114 118 129 151 192 196 197—199 201 202 233 237 252 255 258 267 311 343 363
Property, fine sheaf 381
Property, insertion 57 140
Property, Lusin — Menchoff of  -topology 100 247 342 -topology 100 247 342
Property, Lusin — Menchoff of base 103—106 196—199 201 233 240
Property, Lusin — Menchoff of topology 85 89 90 98 99 101 116 117 120 121 125 126 133 134 196—199 201 233 245 247 248 257 271
Property, M 137 138
Property, measure sweeping 353 429
Property, perfect Lusin-Menchoff 96 97 117
Property, quasi-Lindelof 17 18 148 182 218 248 344 361
Property, Riesz decomposition 329 377 429
Property, Slobodnik 136 137 138
Property, Zahorski 86 90 92 101 126 260 272
Qualitative derivative 300
Quasi-continuous function 408 412
Quasi-Lindelof property 17 18 148 182 218 248 344 361
Quasi-minimum principle 421
Quasi-open set 411
Quasi-solution 418 419
Quasi-superfunction 419 420 422
r- -topology 247 248 274 275 -topology 247 248 274 275
r-basis set 240
r-modification 240—249 275
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



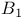 -extension theorem
-extension theorem 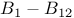 differentiation bases
differentiation bases  -insertion property
-insertion property 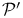 -space
-space  -bounded
-bounded 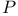 -harmonic space
-harmonic space 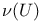 -topology
-topology  -approximately continuous function
-approximately continuous function  -lower semicontinuous regularization
-lower semicontinuous regularization 

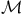 -measurable
-measurable 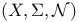
 -=
-=