|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lukes J., Maly J., Zajicek L. — Fine Topology Methods in Real Analysis and Potential Theory |
|
|
 |
| Предметный указатель |
r-topology 240—249 275
Rectangle differentiation basis 165 179 180 201
Reduite 332
Regular point 3 397 392 399
Regular sequence 397
Regular set 3 327 404
Regularization lower semicontinuous 408 332 376
Removable singularity 386 414 432
Resolutive function 355
Resolutive set 355
Riesz decomposition property 329 377 429
Right density differentiation basis 166 179 180 184
s-related topologies 136 137 142 237 246
Saturated 353
Scheinberg’s 228 252 253
Scheinberg’s topology 228 252 253
Semipolar set 18 33
Semiregular point 397 398
Separately continuous function 58 138 306 311
Set, ambivalent 65 240
Set, b-closed 5
Set, finely regular 336 337 400 404 406 426
Set, polar 339 340 361 431
Set, quasiopen 411
Set, r-basis 240
Set, regular 3 327 404
Set, semipolar 18 33 333 343 345 361 376 386 414
Set, subbasic 21
Set, thin at a point 3 9 43 333 335 345
Set, totally thin 17 33 333 343 345 361
Singularity removable 386 414 432
Slobodnik property 136—148
Sorgenfrey topology 15 40 50 62 67 68 92 93 123 235 236
Space,  -harmonic 328 330 331 346 347 360—364 383 396 412 -harmonic 328 330 331 346 347 360—364 383 396 412
Space,  424 430—433 424 430—433
Space, a -topological 91 94 119 120 247
Space, Baire 86 133 136—140 192 236
Space, base operator 5
Space, binormal 85 90 92 93
Space, bitopological 85 92 93
Space, Blumberg 140 141 142 151 236 237 246 364
Space, Cech complete 134 140
Space, cometrizable 133 135
Space, elliptic 359 360
Space, harmonic 328 330 331 347 412
Space, hereditarily, Baire 139 138 151 182 218
Space, perfect 94 111
Space, perfectly binormal 35 96 119
Space, strong Baire 22 60 122 135 139 142 237 246 248 249 343
Space, weak Baire 135 192
Standard H-cone 329 330 332 344 353 354 360 377 424 428
Standard Stolz angle 291
Stolz angle 291
Strict potential 350 393
Strong Baire space 33 60 133 135 139 142—145 237 246 248 249 343
Strong base operator 8
Strong density topology 199 200 307
Strong essential radius condition 67 293
Strong lifting 254
Strongly approximately continuous function 165 200 271 276 307 308
Subbasic set 31
Superdensity differentiation basis 166 179 180 192
Superdensity topology 190 197 247 276 281
Superfunction 401
| Superharmonic function 3 324 325 328 348 350
Sweeping kernel 336 338 432
Symmetric differentiation basis 164 179 180 186 193 198 201 276
Theorem, 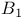 -extension 112 263 266 311 -extension 112 263 266 311
Theorem, abstract in-between 71—75 77—81 95 116 128 280
Theorem, approximation 124 130 131 242
Theorem, asymmetrical in-between 112 116
Theorem, convergence 336
Theorem, Denjoy — Stepanoff 171 172 218
Theorem, density 148 164 168 172 173 208
Theorem, Eilenberg — Saks 267 269
Theorem, Keldych 406
Thin set 3 9 170
Tietze’s condition 32 95
Topological closure 8
Topology, 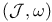 -contingent 258 259 311 -contingent 258 259 311
Topology, 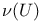 380 382 383 412 424 428 429 380 382 383 412 424 428 429
Topology, 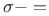 90 94 119 120 247 342 411 90 94 119 120 247 342 411
Topology, ( )-superdensity 192 193 197 270 )-superdensity 192 193 197 270
Topology, a-= 231—239 270
Topology, a.e.- = 230—239 249
Topology, abstract density 212 213—222 224-226 250—254 364
Topology, abstract density = on 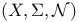 213—222 213—222
Topology, b- = 5
Topology, category density 212 218 221 253
Topology, cometrizable 133 135 188 247 343
Topology, crosswise 7 40 45 67 68 137 138
Topology, density 1 88 92 93 146 148 151 156 158 160 161 237 261 273
Topology, density determined by a filter differentiation basis  204 205 208 210 215 204 205 208 210 215
Topology, density determined by a lower density 208 209
Topology, density detrmined by a differentiation basis  163—189 198 205 228 244 273 275 276 163—189 198 205 228 244 273 275 276
Topology, fine 38 43
Topology, fine boundary 255 257 301 307 311 313 317
Topology, fine in potential theory 3 318 321 325 332 341 343 345 358 360—364 382
Topology, ideal 22 50 138 141 218 251 253
Topology, lifting 223 224—228 251 253
Topology, line 97
Topology, linear density 195 199
Topology, M-contingent 98 311 312
Topology, natural 80 424
Topology, ordinary density 51 167 181 188 189 237 239 245—247 321
Topology, r- = 240—249 275
Topology, S-related 136 137 142 237 246
Topology, Sorgenfrey 15 40 50 62 67 68 92 93 123 235 236 331
Topology, strong density 199 200 307
Topology, superdensity 190 197 247 276 281
Topology, Sverak’s 89 90
Topology, weak 42 200 237 239 241 242 245
Topology, z-ideal 22 146
Totally thin set 17 33
u-continuous function 329
U-quasi-t-continuous function 431
Universally continuous function 329 350
Upper density 210 226
Upper Lebesgue bounded function 263
Upper solution 388
Urysohn’s condition 91 101
Vitali covering 214
Weak Baire space 135 192
Weak topology 42 200 237 239 241 242 245
Weakly  -approximately continuous function 283 284 286 -approximately continuous function 283 284 286
Wiener method 403 404
Wiener solution 403
Z-ideal topology 22 146
Zahorski property 86 90 92 101 126 260 272
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -harmonic
-harmonic 
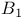 -extension
-extension 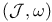 -contingent
-contingent 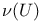
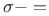
 )-superdensity
)-superdensity