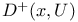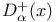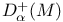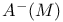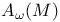|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bhatia N.P., Szego G.P. — Dynamical Systems: Stability Theory and Applications |
|
|
 |
| Предметный указатель |
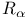 2.14.12 2.14.12
 2.13.2 2.13.6 2.13.2 2.13.6
Action: 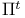 1.1.1 1.1.1
Albrecht, F. 1.8.6
Antosiewics, H.A. 2.7.25 2.11.40 2.12.28 3.6.33
Arzela, C. 3.1.7
Ascoli, G. 3.1.7
Attraction (compact sets) 1.5.6 2.6.1
Attraction (compact sets), conditions for 3.7.11
Attraction (compact sets), global 1.5.6 1.9.9 1.9.10
Attraction (compact sets), global weak 1.9.9 1.9.10
Attraction (compact sets), negative 1.5.10
Attraction (compact sets), region of see “Region”
Attraction (compact sets), relative 1.5.6
Attraction (compact sets), stable 1.5.16 1.5.40 1.6.33
Attraction (compact sets), uniform 1.5.6 1.5.27 1.5.28 2.6.1
Attraction (compact sets), unstable 1.5.15 1.6.33
Attraction (compact sets), weak 1.5.16 1.5.40 1.6.33
Attraction (motion) 1.11.11
Attraction (sets) 1.6.11 1.6.21 1.6.22 1.6.23 1.6.25 2.12.10
Attraction (sets), (uniformly) stable 1.6.26 1.6.30 1.6.33
Attraction (sets), (uniformly) stable semi 1.6.26 1.6.28 1.6.29 1.6.33
Attraction (sets), (uniformly) stable semi, conditions for 1.7.7
Attraction (sets), (uniformly) stable uniform 1.6.26 1.6.33
Attraction (sets), (uniformly) stable, conditions for 1.7.8
Attraction (sets), conditions for 2.12.16
Attraction (sets), equi 1.6.11 2.12.12
Attraction (sets), equi, conditions for 2.12.23 2.12.24
Attraction (sets), semi 1.6.11 1.6.19 1.6.22 1.6.25 2.12.12
Attraction (sets), semiweak 1.6.11 1.6.18 1.6.22 2.12.12
Attraction (sets), uniform 1.6.11 2.12.10
Attraction (sets), weak 1.6.11 1.6.20 1.6.22 2.12.12
Auslander, J. 2.3.18 2.6.21 2.7.12 2.7.25 2.8.14 2.11.40 2.13.31 235 2.14.16
Axioms 1.1.2 2.1
Axioms, continuity 1.1.2 iii) 2.1.3 2.1.3'
Axioms, homomorphism 1.1.2 ii) 2.1.2 2.1.2'
Axioms, identity 1.1.2 i) 2.1.1 2.1.1'
Barbashin, E.A. 2.7.25 2.11.40 300 3.6.33
Bebutov, M.V. 2.11.40 3.1.70
Beckenback, E. 3.1.70
Bellman inequality 3.1.21 3.1.24
Bellman, R. 3.1.70
Bendixson, I. 1.4.14
Bhatia, N.P. 1.3.35 1.5.43 1.6.52 1.7.16 1.9.11 2.3.18 2.6.21 2.7.25 2.8.14 2.11.40 3.8.33
Birkhoff, G.D. 1.1.9 1.2.48 1.3.35 1.10.12 163 2.9.14
Bochner, S. 2.10.17
Bohr, H. 2.10.17
Brauer, F. 3.1.47 3.1.70
Bronshtein, I.V. 301 305
Brown Theorem on the union of open n-cells 2.8.9
Brown, M. 2.8.14
Budak, B.M. 300
Caratheodory condition for the existence of solutions of ODE 3.1.11
Caratheodory, C. 249 250 3.1.15 3.1.70
Cesari, L. 1.5.43
Chetaev, N. 1.11.13 3.6.33
Coddington, E.A. 3.1.70 313
Conti extendability condition 3.1.59
Conti, R. 275
Continuity axiom for dynamical system 1.1.2 iii) 2.1.3 2.1.3'
Continuity conditions for solutions of ODE 3.1.26
Critical points of a dynamical system 1.2.7—1.2.18 18 1.2.24
Critical points of a real-valued function 3.8.5
Critical points of a real-valued function, existence of 3.8.25
Critical points of a real-valued function, infinite 3.8.5
Curve 3.4.2
Curve, maximal 3.4.2
Curve, right-family of 3.4.2
Desbrow, D. 2.6.21
Deysach, L.G. 2.10.17
Differentiability conditions for solutions of ODE 3.2.24 3.2.29
Dugundji, J. 1.2.48 2.11.40 2.12.28
Dynamical system 1.1 2.1
Dynamical system, completely unstable 2.11.4
Dynamical system, continuous 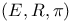 or or 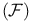 1.1.1 1.1.1
Dynamical system, continuous 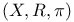 2.1 2.1
Dynamical system, continuous 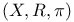 , defined by ODE 3.1 3.1.67 , defined by ODE 3.1 3.1.67
Dynamical system, discrete 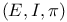 1.1.8 1.2.28 1.1.8 1.2.28
Dynamical system, dispersive 2.11.5 2.11.15 2.11.17 2.11.34 2.11.35 2.11.38
Dynamical system, dispersive (without uniqueness) 3.3.4
Dynamical system, L-stable 2.11.2
Dynamical system, L-unstable 2.11.2
Dynamical system, L-unstable, on the space of continuous functions, 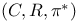 3.5.8 3.5.8
Dynamical system, local 3.3.1
Dynamical system, parallelizable 2.11.6 2.11.20 2.11.22 2.11.38 2.12.20 2.12.22
Dynamical system, section of 2.11.18—2.11.20 2.11.27
Dynamical system, time-varying 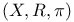 3.5.13 3.5.13
Dynamical system, wandering 2.11.4
Equation of the perturbed motion 3.6.33
Equicontinuous family of functions 247
Equivalent differential equations 3.1.66 3.1.67
Euclidean distance 0.1.3
Euclidean n-space (E) 0.1
Euclidean norm 0.1
Existence conditions for solutions of ODE 3.1.8 3.1.11 3.1.12
Existence conditions for solutions of ODE, global 3.1.52 3.1.59 3.1.61 3.1.62
Extension theorem 3.8.28
Flow 1.1.1
Flow without uniquenes s 3.3.3
Fukuhara, M. 3.2.20 291 3.2.31 318 3.4.33
Function, (positive) (negative) definite, for closed sets 0.2.9
Function, (positive) (negative) definite, for compact sets 0.2.4
Function, (positive) (negative) definite, for compact sets, conditions for 0.3.3
Function, (positive) (negative) semidefinite, for compact sets 0.2.1
Function, (weakly) (semi) definite, for closed sets 0
Function, admissible 3.5.7
Function, increasing 0.2.5
Function, indefinite, for closed sets 0.2.13
Function, indefinite, for compact sets 0.2.1
Function, Liapunov 3.6.75 (see also “Liapunov”)
Function, Lipschitz continuous 3.1.16
Function, radially unbounded 0.2.6
Function, strictly increasing 0.2.5
Function, uniformly bounded 0.2.11
Function, uniformly unbounded 2.7.13
Function, weakly positive definite 271
Funnel see “Solution Funnel”
Geiss, G.R. 3.6.33
General control system 3.3.6
Generalized recurrent set R see “Set”
Gottschalk, W.H. 1.1.9
Grabar, M.I. 3.1.76
Gronwall inequality 3.1.21 3.1.24
Gronwall, T.H. 3.1.70
Group 1.1.5
Group property 1.1.2 ii)
Group, commutative 11
Hadamard, J. 3.6.33
Hajek, O. 3.1.70
Halkin, I.A. 1.11.13 2.7.25
Halm, W. 1.11.13 2.7.25 3.6.33
Hartman, P. 3.1.70 283
Hedlund, G.A. 1.1.9
Hocking, J. 2.2.17
Homomorphism axiom 1.1.2 ii) 2.1.2. 2.1.2'
Ingwerson, D.R. 3.8.33
Instability, complete 1.6.39 1.6.50
Instability, complete, for compact sets 1.5.13 1.5.38 1.5.39
Instability, complete, for compact sets, conditions for, in ODE 3.6.22
Instability, global, for compact sets 3.6.31
Instability, global, for compact sets, conditions for, in ODE 3.6.32 3.8.27
Instability, Lagrange (L) 1.5.3 2.11.1
Instability, Liapunov, for compact sets 1.5.6. 2.6.1
Instability, Liapunov, for compact sets, conditions for, in ODE 3.6.23
Instability, Liapunov, for sets 1.6.34 1.6.35
Instability, ultimate 1.6.37 1.6.47
Instability, ultimate complete 1.6.39 1.6.40 1.6.51
Instability, ultimate weak 1.6.37 1.6.38 1.6.46
Instability, ultimate weak complete 1.6.39 1.6.41 1.6.49
Instability, weak 1.6.34 1.6.36 1.6.44
| Instability, weak complete 1.6.39 1.6.41 1.6.48
Invariant sets 1.2.29—1.2.41 1.3.13 1.4.12 1.4.13 1.5.24 1.5.40 1.8.2. 116 3.4.16 3.4.18 3.4.22 3.4.23
Invariant sets, (positively) (negatively) strongly 2.7.9 2.8.1 3.3.14 3.7.2
Invariant sets, (positively) (negatively) weakly 3.3.14 3.3.15 3.4.16 3.4.17 3.4.20 3.4.21 3.4.24 3.4.25
Invariant sets, compact 2.9.1
Invariant sets, semi 1.2.29
Invariant sets, U. 3.4.32
Jones, G.S. 3.1.70
Kamke general uniqueness theorem 3.1.46
Kamke, E. 3.1.46 3.1.70 283—285 3.2.31
Kneser theorem 3.2.14 3.4.55
Kneser, H. 287 3.2.31 318 3.4.35
Krasovskii, N.N. 2.7.25 3.6.33
Krecu, V.I. 301
Kudaev, M.B. 366
Kurzweil, J. 2.7.25 3.6.33
La Salle, J.P. 147 3.7.16
Lagrange stability see “Stability”
Lazer, A.C. 1.5.43
Lefschetz, S. 1.3.35 1.5.43 2.2.17 2.8.14
Leighton, W. 3.8.33
Levinson, N. 3.1.70 313
Lewis, D.C. 3.6.33
Liapunov functions 1.7 3.6.25
Liapunov functions, existence of 2.7.1. 2.7.14 2.7.17 2.7.23 2.7.26
Liapunov functions, properties of 2.7.9 2.8.1 2.8.5
Liapunov second method 3.6.24
Liapunov stability see “Stability”
Liapunov, A.M. 1.5.43 1.7.16 1.11.13 2.7.25 2.6.33
Limit sets, high prolongational, 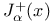 2.14.1 2.14.4 2.14.12 2.14.1 2.14.4 2.14.12
Limit sets, positive (negative), of sets 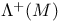 ( (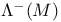 ) 1.3.1 1.3.32 ) 1.3.1 1.3.32
Limit sets, positive (negative), of trajectories  ( (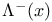 ) 1.3.1—1.3.31 1.5.4. 2.2.5—2.9.9. 2.3.14 2.5.8 2.5.11 2.5.12 2.10.14 2.10.15 3.7.10 2.5.7 ) 1.3.1—1.3.31 1.5.4. 2.2.5—2.9.9. 2.3.14 2.5.8 2.5.11 2.5.12 2.10.14 2.10.15 3.7.10 2.5.7
Limit sets, prolongational, 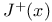 , , 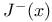 2.3.6—2.3.14 2.11.7 2.11.15 2.11.37 2.3.6—2.3.14 2.11.7 2.11.15 2.11.37
Lipschitz condition 3.1.17
Lipschitz, R. 3.1.16
Map, c-c 2.13.10
Map, cluster 2.13.9
Map, multivalued 3.3.3
Map, phase 115
Map, transitive 2.13.7
Markov, A.A. 1.1.9 2.10.17
Markus, L. 2.8.14
Massera, J.L. 2.7.25
Maximal interval of existence of solutions of ODE 251 3.1.13 3.2.26
Maximal interval of existence of solutions of ODE, semicontinuity of 3.2.30
Mendelson, P. 1.5..43
Metric Space X 0.1
Minimal sets 1.2.42—1.2.47 1.3.23 1.3.24 1.3.26 1.5.41 2.9.1—2.9.10 2.9.13 2.10.14
Minimal sets, compact 2.9.7
Minimal sets, non compact 2.9.13
Minkevich, M.I. 299
Montel, P. 3.1.70
Montgomery, D. 1.1.9
Motion 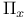 1.1.1 115 1.1.1 115
Motion 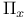 , (positively) (negatively) Liapunov stable 1.11.1 , (positively) (negatively) Liapunov stable 1.11.1
Motion 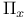 , (positively) Liapunov (uniformly) stable, with respect to a set 1.11.9 2.10.12 2.10.15 , (positively) Liapunov (uniformly) stable, with respect to a set 1.11.9 2.10.12 2.10.15
Motion 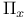 , (positively) Liapunov uniformly stable 1.11.3 1.11.5 2.10.12 , (positively) Liapunov uniformly stable 1.11.3 1.11.5 2.10.12
Motion 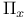 , attracting 1.11.10 , attracting 1.11.10
Motion 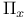 , Lagrange stable (L-stable) 2.5.1 , Lagrange stable (L-stable) 2.5.1
Motion 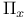 , Lagrange stable (L-stable), negatively 2.5.1 2.10.12 , Lagrange stable (L-stable), negatively 2.5.1 2.10.12
Motion 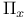 , Lagrange stable (L-stable), positively 2.5.1 2.10.14 2.10.15 , Lagrange stable (L-stable), positively 2.5.1 2.10.14 2.10.15
Motion 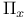 , Lagrange unstable 2.11.1 , Lagrange unstable 2.11.1
Motion 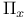 , negatively Poisson stable ( , negatively Poisson stable (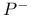 -stable) 1.10.4 1.10.7 2.5.4 -stable) 1.10.4 1.10.7 2.5.4
Motion 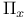 , periodic 1.2.19 2.4.2. 2.5.12 2.5.8 , periodic 1.2.19 2.4.2. 2.5.12 2.5.8
Motion 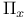 , periodic, almost 1.10.2 2.10.5 , periodic, almost 1.10.2 2.10.5
Motion 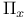 , Poisson stable (P-stable) 1.10.4 1.10.7 2.5.4 , Poisson stable (P-stable) 1.10.4 1.10.7 2.5.4
Motion 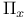 , positively Poisson stable ( , positively Poisson stable (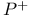 -stable) 1.10.4 1.10.7 2.5.4 2.5.7 2.5.11 -stable) 1.10.4 1.10.7 2.5.4 2.5.7 2.5.11
Motion 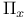 , recurrent 1.10.3 2.9.4—2.9.12 2.10.10 2.10.11 , recurrent 1.10.3 2.9.4—2.9.12 2.10.10 2.10.11
Nagumo, M. 3.2.20
Nemytskii, V.V. 1.1.9 1.2.48 1.3.35 2.5.15 2.9.14 2.10.17 2.11.40 365
Norm 0.1.1 0.1.2
Norm, Euclidean 0.1.1
Olech, C. 3.1.70 357 3.8.33
Operator D 2.13.2 2.13.6
Operator S 2.13.2 2.13.5 2.13.6
Orbit 1.2.1
Osgood uniqueness condition 3.1.51
Osgood, W. 3.1.51 3.1.61
Papush, N.P. 365
Parametric form of ODE 3.5.2
Peano condition for the existence of solutions of ODE 3.1.8
Peano, G. 3.1.8
Peixoto, M. 3.1.70
Period 18 2.4.2
Periodic motion 1.2.19—1.2.25 1.3.21 1.3.25 1.10.1 2.4.2 2.5.8 2.5.12
Periodic motion, almost 1.10.2 2.10.5
Perron, O. 3.1.51
Persidskii, K.P. 2.7.25 3.6.33
Persidskii, S.K. 2.7.25
Petrovskii, I.G. 1.9.11
Phase map 115
Phase space 115
Pliss, A. 1.8.6
Poincare, H. 1.3.35 1.4.14 3.6.33
Point, (equilibrium), (stationary), (rest), (critical), of dynamical systems or ODE 1.2.7
Point, critical, of real-valued functions see “Critical point”
Point, egress 1.8.1
Point, egress, strict 1.8.1
Point, existence of 1.2.14 1.2.16 1.9.2 1.9.4—1.9.6 2.8.6—2.8.8
Point, negative (alpha) limit 1.3.1
Point, positive (omega) limit 1.3.1
Point, wandering 2.11.3 2.11.28 2.11.32
Point, wandering, non 2.11.3 2.14.7
Poisson stability see “Stability”
Prolongation of compact global weak attractors 1.9.9
Prolongation of compact weak attractors 1.5.42 2.6.15
Prolongation of sets, 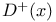 , ( , ( ) 1.4.1 ) 1.4.1
Prolongation, first positive (negative), 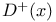 , ( , ( ) 1.4.1 2.3.1 ) 1.4.1 2.3.1
Prolongation, first positive relative, 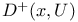 2.15.1 2.15.1
Prolongation, higher, 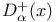 2.13.15 2.14.4 2.14.11 2.13.15 2.14.4 2.14.11
Prolongation, uniform first positive, 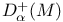 2.13.28 2.13.28
Prolongational limit set see “Limit set”
Pugh, C. 3.2.20
Quasi order 2.14.15
R' 2.14.12 2.14.13
Recurrence 1.10.3 2.9.7—2.9.12 2.10.10 2.10.11
Region of asymptotical stability (for compact sets) 1.5.16 2.7.11 2.8.10
Region of attraction (for compact sets), A(M) 1.5.6 1.5.11 1.5.14 2.6.3
Region of attraction (for compact sets), A(M), (for sets) 1.6.12 1.6.31 1.6.32 2.12.13
Region of repulsion (for compact sets), 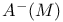 1.5.10 1.5.10
Region of weak attraction (for compact sets), 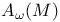 1.5.6 2.6.3 2.8.6 1.5.6 2.6.3 2.8.6
Region of weak attraction (for compact sets), 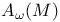 (for sets) 1.6.12 1.6.16 2.12.13 (for sets) 1.6.12 1.6.16 2.12.13
Rest point see “Point”
retract 1.8.3 2.8.5
Retraction 1.8.3
Roxin, E. 1.7.16 302 303 304 316
S 2.13.2 2.13.5 2.13.6
Section 2.11.18—2.11.20 2.11.27
Seibert, P. 2.3.18 2.6.21 2.7.12 2.7.25 2.8.14 2.13.31
Sell, G. 2.10.17 298 306 3.5.21
Semigroup of multivalued mappings 3.3.5
Semiinvariant set 1.2.29
Semitrajectory 1.2.1
Set, 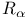 2.14.12 2.14.12
Set, (positive) (negative) limit 1.3.1 2.2.5
Set, (positively) (negatively) (semi) invariant 1.2.29 (see also “Invariant set”)
Set, (positively) (negatively) strongly invariant 3.3.14
Set, (positively) (negatively) weakly invariant 3.3.14 3.3.15 3.4.16 3.4.17 3.4.20 3.4.21
Set, attainable 3.2.10
Set, closed, with a compact vicinity 0.2.2 0.2.3
Set, generalized recurrent, R 2.14.7—2.14.10 2.14.13
Set, minimal 1.2.42 2.2.4
Set, R' 2.14.12 2.14.13
Set, Reachable 3.2.10
Set, relatively dense, of numbers 0.2.14
Sibirskii, K.S. 301
Solution Funnel 3.2.10
Solution Funnel, boundary of 3.2.21
Solution Funnel, bounded 3.7.10
Solution Funnel, continuity of 3.2.12
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



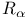

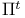
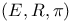 or
or 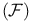
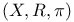
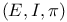
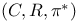
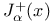
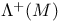 (
(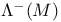 )
)  (
(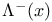 )
) 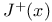 ,
, 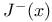
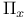
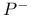 -stable)
-stable) 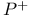 -stable)
-stable) 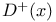 , (
, ( )
)