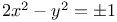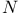 (for Numerus) by Xylander, Bachet, Fermat and others 38 (for Numerus) by Xylander, Bachet, Fermat and others 38
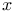 for unknown quantity, originated with Descartes 50 n. for unknown quantity, originated with Descartes 50 n.
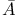 ryabhata 281 ryabhata 281
Ab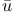 Тl Ч Faraj 1 Тl Ч Faraj 1
Ab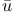 Тl Ч Waf Тl Ч Waf al Ч B al Ч B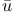 zj zj n n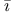 6 19 6 19
Achm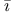 m Papyrus 45 m Papyrus 45
Addition, BombelliТs sign for 22
Addition, expressed in Dioph. by juxtaposition 42
Addition, first appearance of 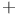 49 n. 49 n.
Ahmes 112
al Ч Karkh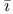 5 41 5 41
al Ч Karkh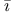 5 41 5 41
al Ч Khuw razm razm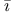 , Muhammad b. M , Muhammad b. M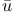 s s 34 50 34 50
Alfraganus 20
Algebra, three stages of development 49Ч51
Algebraical notation, Bachet and Fermat 38
Algebraical notation, beginnings of modern signs 49Ч50 n.
Algebraical notation, Bombelli 22 38
Algebraical notation, Diophantus 34Ч39 41Ч44
Algebraical notation, earlier Italian algebraists 38
Algebraical notation, Vieta 38 39 50
Algebraical notation, Xylander 38 48
Aljabr 64
Almuk bala 64 bala 64
Amthor 122
Anatolius 2 18
Andreas Dudicius Sbardellatus 17 25
Angelas Vergetius 16
Anthology, arithmetical epigrams in 113Ч114
Anthology, indeterminate equations in 114
Anthology, on Diophantus 3
Apollonius of Perga 5 6 12 18 122
Approximations, Archimedes 278Ч279
Approximations, Diophantus 95Ч98
Approximations, Pythagoreans 117Ч118 278
Arabian scale of powers of unknown compared with that of Diophantus 40 41
Arabic versions and commentaries 19
Archimedes 11 12 35 278 279 290
Archimedes, Arenarius 35 122
Archimedes, Cattle Ч Problem 121Ч124 279
Archimedes, Codex Paris, of 48
Arenarius of Archimedes 35 122
Arithmetica of Diophantus, conspectus of problems in 260Ч266
Arithmetica of Diophantus, different titles by which known 4Ч5
Arithmetica of Diophantus, division into Books 5 17Ч18
Arithmetica of Diophantus, lost Books 5Ч12
Arithmetica of Diophantus, notation in 32Ч53
Arithmetical progression, summation of 248Ч249
Ars rei et census 20
Auria, Joseph 15 18
Bachet 12 16 17 21 22 25 26Ч29 35 45 48 80Ч82 87 101 107 109 110 140 173 196Ч197 213 220 230 232 234Ч235 246 271 273 287 293
Back-reckoning 56 89 93
Baillet 45 n.
Bessarion, Cardinal 17 20
Bh skara 281 skara 281
Bianchini 20
Billy, Jacques de 28 165 166 184 221 267 304 308 320 321 326
Bodleian MS. of Euclid 35
Bodleian MSS. of Dioph 15 34 35
Bombelli, Algebra of 21 22
Bombelli, Rafael 11 27
Bombelli, symbols used by 22 38
Brahmagupta 281
Brancker, Thomas 286 n.
Brouncker, William, Viscount 286 288
Camerarius, Joachim 21
Cantor, Moritz 3 n. 6 63 112 118 120 125 281
Cardano 21 23 40
Cattle Ч Problem of Archimedes 11 12 121Ч124 279
Cauchy 188 274
Censo, or Zensus, = square 40 41
Charmides, scholiast to, in 113 121Ч122
Chasles, n Cleonides 16 n.
Coefficient, expressed by 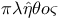 , multitude 64 n. , multitude 64 n.
Colebrooke 6 281
Cosa, =the unknown 22 40
Coss 23
Cossali 1 21 40 41 140
Cracow MS. of Dioph 514 18
Cube, EulerТs solution of problem of finding all sets of three cubes having a cube for their sum 329Ч334
Cube, FermatТs extensions, ibid., a cube cannot be the sum of two cubes 144
Cube, sign for cube of unknown or 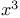 38 129 38 129
Cube, VietaТs formulae for transforming the sum of two cubes into a difference of two cubes and vice versa 101Ч103
Cubic equation, simple case of 66Ч67 242
Cuttaca (УpulveriserФ), Indian method of 283
Definitions of Diophantus 32 38 39 129Ч131
Denominator 137
Descartes 271 273
Descartes notation 50 n.
Determinate equations, a particular cubic 66Ч67
Determinate equations, mixed quadratics 59Ч65
Determinate equations, of first and second degrees 58
Determinate equations, pure 58Ч59
Determinate equations, simultaneous equations leading to quadratics 66
Dionysius 2 n. 9 129
Diophantus, commentators and editors 18Ч31
Diophantus, date 1Ч2
Diophantus, Dioph. not inventor of algebra 111Ч116
Diophantus, epigram on 3
Diophantus, his extensions of theory of polygonal numbers 127
Diophantus, his work a collection in best sense 124
Diophantus, in Arabia 5Ч6 19
Diophantus, methods of solution 54Ч98
Diophantus, MSS. of 14Ч18
Diophantus, nor of indeterminate analysis 115Ч124
Diophantus, notation of 32Ч53
Diophantus, numbers as sums of four squares 110
Diophantus, numbers not sum of three squares 108Ч109
Diophantus, numbers which are not the sum of two squares 107Ч108
Diophantus, on numbers which are the sum of two squares 105Ч106
Diophantus, other assumptions 103 sqq.
Diophantus, porisms of 3 8Ч10 99Ч101
Diophantus, spelling of name 1
Diophantus, theorems in theory of numbers 110
Diophantus, works 3Ч13
Diophantus, УPseudepigraphusФ 31
Division, how represented by Dioph. 44Ч47
Doppelmayer 20 n.
Double-equations (for making two expressions in 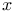 simultaneously squares) 11 73Ч87 91Ч92 simultaneously squares) 11 73Ч87 91Ч92
Double-equations (for making two expressions in 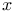 simultaneously squares), double equations for making one expression a square and another a cube 91Ч92 simultaneously squares), double equations for making one expression a square and another a cube 91Ч92
Double-equations (for making two expressions in 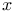 simultaneously squares), general rule for solving 73 146 simultaneously squares), general rule for solving 73 146
Double-equations (for making two expressions in 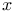 simultaneously squares), two expressions of Double-equations (for making two expressions in simultaneously squares), two expressions of Double-equations (for making two expressions in 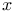 simultaneously squares), first degree 73Ч80 80Ч82 simultaneously squares), first degree 73Ч80 80Ч82
Double-equations (for making two expressions in 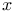 simultaneously squares), two expressions of second degree or one of first and one of second 81Ч87 simultaneously squares), two expressions of second degree or one of first and one of second 81Ч87
Dudicius Sbardellatus, Andreas 17 25
Egyptians, beginnings of algebra, haw-calculations 111Ч112
Egyptians, hau, sign for 37
Egyptians, method of writing fractions 112
Egyptians, names for successive powers 41
Eisenlohr 112 n.
Enestr m 63 n. 286 m 63 n. 286
Epanthema of Thymaridas 114Ч116
Epigrams, arithmetical, in Anthology 113Ч114
Epigrams, arithmetical, in Anthology, on Diophantus 3
Epigrams, arithmetical, in Anthology, one in Diophantus (V. 30) 124
Equality, abbreviation for 47Ч48
Equality, sign in Xylander 48
Equality, the sign = due to Recorde 50 n.
Equations see Determinate Indeterminate Double Triple etc.
Eratosthenes 121
Euclid 8 11 12 19 63 117 124 132 144 191
Eudoxus 124
Euler 56 71Ч72 83Ч85 86 90 10n. 102 107 110 145 151 160 162 178 181Ч182 188 224 236 241 242 268 272 274 275 286 288Ч292 294 297 299
Euler, J. A. 360
Euler, Supplement 329Ч379 passim
Eutocius 5 6
Exponents, modem way of writing due to Descartes 50 n.
Fakhr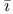 5 41 5 41
Fermat 28 29 30 38 78 90 101 102 103 106 107 108 109 110 144Ч145 163 173 179Ч180 182 183 184 188 190Ч191 197 202 204 205 213Ч214 218 220 223 229 230 231 232 233 235 236 239 240 241 242 246 254
Fermat, 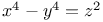 cannot be solved in integers 224 293Ч297 cannot be solved in integers 224 293Ч297
Fermat, Fermat on numbers which are, or are not, the sums of two, three, or four squares respectively 110 267Ч275
| Fermat, FermatТs Уtriple-equationsФ 321Ч328
Fermat, on equation 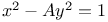 285Ч287 285Ч287
Fermat, on numbers of form 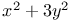 275 275
Fermat, on numbers of form 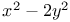 or or 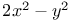 276Ч277 276Ч277
Fermat, on numbers of of form 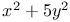 276 277 276 277
Fermat, problems on right-angled triangles 204Ч205 n. 218Ч219 220 229 230 231Ч233 235 236 239Ч240 297Ч318
Fermat, Supplement 267Ч328 passim 364
Fermat, Уgreat theorem of FermatФ 144Ч145 n.
Fr nicle 102 n. 276 277 285 287 295Ч297 309 310 313 314 nicle 102 n. 276 277 285 287 295Ч297 309 310 313 314
Fractions, representation of, in Diophantus 44Ч47
Fractions, sign for 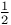 45 45
Fractions, sign for 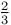 45 45
Fractions, sign for submultiple 45Ч47
G nther 6 278 279 nther 6 278 279
Gardthausen 35 36
Geminus 4
Georg v. Peurbach 20
Georgius Pachymeres 18 19 31 37
Girard, Albert 30 106
Gnomons 125
Gollob 14 18
Grammateus (Schreiber), Henricus 49 n. 50
Greater and less, signs for 50 n.
H rigone 50 n. rigone 50 n.
hankel 6 54Ч55 108 281 283 284 286
Harriot 50 n.
Hau ( = УheapФ), the Egyptian unknown quantity 37 112
Heiberg 35 48 118 205
Henry, C. 13 28
Heron 12 13 35 36 43 44 45 63 129
Hippocrates of Chios 63 124
Holzmann, Wilhelm see Xylander
Hultsch 2 n. 3 4 9 10 11 12 19 35 36 37 47 63 118 122 253
Hydruntinus, Ioannes 16
Hypatia 5 6 14 18
Hypsicles 2
Hypsicles, on polygonal numbers 125Ч126 252 253
Iamblichus 2 3 37 49 50 115Ч116 126
Ibn ab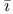 UsaibiТa 19 UsaibiТa 19
Ibn al Ч Haitham 19
Identical formulae in Diophantus 104 105
Indeterminate equations, 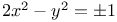 solved by Pythagoreans 117Ч118 278 310 solved by Pythagoreans 117Ч118 278 310
Indeterminate equations, double-equations for making one expression a square and another a cube 91Ч92
Indeterminate equations, double-equations for making two expressions simultaneously squares 11
Indeterminate equations, double-equations for making two expressions simultaneously squares, two expressions of first degree 73Ч80 80Ч82
Indeterminate equations, double-equations for making two expressions simultaneously squares, two of second degree, or one of second and one of first 81Ч87
Indeterminate equations, how to find fresh solutions when one is known 68Ч70
Indeterminate equations, indeterminate equations in Anthology 114
Indeterminate equations, other Greek examples 118Ч121
Indeterminate equations, rule for solving double-equations in which two expressions are to be made squares 73 146
Indeterminate equations, single, of higher degrees 87Ч91
Indeterminate equations, single, of second degree 67Ч73
Indian method 12Ч13 21
Indian solution of 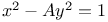 281Ч285 290 292 281Ч285 290 292
Inventum Novum of J. de Billy 28 165 184 198 204 205 n. 230 231 239
Inventum Novum of J. de Billy, Supplement 267Ч328 passim
Ioannes Hydruntinus 16
Ish q b. Y q b. Y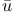 nis 19 nis 19
Italian scale of powers 40 41
jacobi 108 n. 288
Kausler 31
Kaye, G. R. 381
KaТb, Arabic term for cube of unknown 41 n.
Kenyon 45
Konen 378 379 281 385 386 388 391
kronecker 388
Krumbiegel 113
Kummer 145 n.
Lagrange 73 110 188 373 373 274 275 276 277 285 387 388 290 293 299 300
Lato, УsideФ 40 n.
legendre 107 n. 109 188 273
Lehmann 35
Lejeune Ч Dirichlet 145 288
Leon 124
Leonardo of Pisa 11 41 120
Less and greater, signs for 50 n.
Limits, approximation to 95Ч98
Limits, method of 57 94 95
Logistica speciosa and Logistica numerosa distinguished by Vieta 49
Loria 63 n. 157 168 175 176 195 197 207 340 241
Lousada, Abigail 31
Luca Paciuolo 31 40
M l, Arabic term for square 41 n. l, Arabic term for square 41 n.
Madrid MS. 14 15 16
Manuscripts of Diophantus 14Ч18
Maximus Planudes 13 14 19 21 31 43 44 45 46 48
Measurement of a Circle (Archimedes) 122
Mendoza 17
Metrica of Heron 43 44 45 63 129
Metrica of Heron, MS. of 118
Metrodorus 5 113
Minus, DiophantusТ sign for 41Ч44 130
Minus, DiophantusТ sign for, BombelliТs abbreviation 22
Minus, DiophantusТ sign for, modern sign for 49
Minus, DiophantusТ sign for, same sign in HeronТs Metrica 43 44
Minus, DiophantusТ sign for, VietaТs sign for difference between (= for  ) 50 n. ) 50 n.
Montchall, Carl v 18
Montucla 28
Moriastica of Diophantus 3Ч4
Muhammad b. M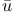 s s al ЧKhuw al ЧKhuw razm razm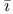 34 50 34 50
Multiplication, signs for 50 n.
Murr, Ch. Th. v 10
Negative quantities not recognised by Diophantus as real 53Ч53
Nesselmann 6Ч10 21 35 26 39 34 49Ч51 55Ч58 67 87 89 93 108 140 173 304 207 252 329
Nicomachus 3 136 127
Notation, algebraic, DiophantusТ notation 33Ч49 51Ч53
Notation, algebraic, three stages 49Ч51
Nu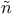 ez 23 ez 23
Numbers which are the sum of two squares 105Ч107 368Ч371
Numbers which are the sum of two squares, corresponding theorem for triangles, pentagons, etc 188 373
Numbers which are the sum of two squares, numbers not square are the sum of two, three or four squares 110 373 374
Numbers which are the sum of two squares, numbers which are not 107Ч108 371Ч373
Numbers which are the sum of two squares, numbers which are the sum of three squares 373Ч373
Numbers which are the sum of two squares, numbers which are the sum of three squares, numbers which are not 108Ч109 373
Numerus, numero, term for unknown quantity 38 40
Oughtred 50 n.
Ozanam 288
Pachymeres, Georgius 18 19 31 37
Paciuolo, Luca 21 40
Pappus 11 13
Papyrus Rhind 113
Papyrus Rhind, Berlin papyrus 6619 113
Paris MSS. of Diophantus 15 16 18
Pazzi, A. M. 31
Pell, John 31 386 288
Peurbach, G. von 20
Philippus of Opus on polygonal numbers 125
Planudes, Maximus 13 14 19 21 31 43 44 45 46 48
Plato 4 38 111 113 116 125
Plus, signs for 23 49
Plus, signs for, expressed in Diophantus by juxtaposition 39
Plutarch 137
Polygonal Numbers, began with Pythagoreans 124Ч125
Polygonal Numbers, DiophantusТ extensions 137
Polygonal Numbers, figured by arrangement of dots 125
Polygonal Numbers, Hypsicles on 125Ч136 353 353
Polygonal Numbers, sketch of history of subject 124Ч127
Polygonal Numbers, treatise on 3 11Ч12 247Ч259
Porisms of Diophantus 3 8Ч10 99Ч101 301 303 314
Poselger 30 98
Powers of unknown quantity and signs for 37Ч39 139
Powers of unknown quantity and signs for, Egyptian scale 41
Powers of unknown quantity and signs for, Italian and Arabian scale (multiplicative) contrasted with Diophantine (additive) 40Ч41
Proclus 4 113 116 117 118 242
Psellus 2 14 18 41 111
Ptolemy 18 44
Pythagoreans 3
Pythagoreans on rational right-angled triangles 116 24 2
Pythagoreans, on indeterminate equation 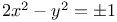 117Ч118 378 310 117Ч118 378 310
Pythagoreans, on polygonal numbers 134Ч135
|
 |
|
ќ проекте
|
|
ќ проекте



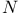 (for Numerus) by Xylander, Bachet, Fermat and others
(for Numerus) by Xylander, Bachet, Fermat and others 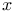 for unknown quantity, originated with Descartes
for unknown quantity, originated with Descartes 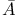 ryabhata
ryabhata 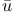 Тl Ч Faraj
Тl Ч Faraj  al Ч B
al Ч B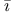
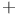
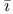
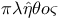 , multitude
, multitude 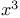
 m
m 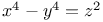 cannot be solved in integers
cannot be solved in integers 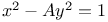
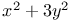
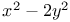 or
or 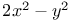
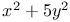
 nicle
nicle 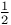
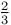
 nther
nther 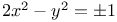 solved by Pythagoreans
solved by Pythagoreans  )
) 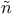 ez
ez