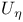Hoelder's inequality 12.3
Homogeneous 24
Homomorphism of Riesz spaces 22
Ideal of 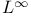 20B 20B
Ideal of a Riesz space (= solid subspace) 18
Image of a (tight) upper gauge 244 28.11
Image of a map 28.17
Image of a measure 28A
Image of a tight measure 28C
Image under a morphism 28.18
Increasing 24
Increasing seminorm 4.7 see 5.9
Independent random variables 33C 33.4
Inductive limit and system of integration lattices 42
Inductive limit and system of uniformities 5A
Inequalities of the mean 20.1
Inner regular weak upper gauge 9.12
Integrability criteria 19A
Integrable fields of measures and upper gauges 25A
Integrable functions and sets 7C
Integrable functions and sets, characterization 9B
Integrable p-integrable functions 12.8
integral see "Ementary integral" "Integration"
Integral Daniell 10A 11C
Integral of a field of measures and upper gauges 25A-C see
Integral of a function 1A 2 10A
Integral of a weakly compact linear map 11C
Integral representation of linear maps 37.5 37B 38B
Integral, Bochner 10A 11C
Integral, compactness properties 10B
Integral, Pettis 11A
Integral, range 10.3—10.5
Integral, Riemann 1A 2 36
Integration see "Integral"
Integration domain 1B 8
Integration lattice 1B 3
Integration lattice of step functions over a clan 1.1
Integration lattice, countably generated 1.3 see 5.12 13.9 35.3
Integration lattice, generated by a family of functions 1.3
Integration of a disintegrated measure 36B
Integration of a field 25A-C 26A-B
Integration of a linear map 11A C
Integration of a measure defined by a density 22B
Integration of a product measure 27B
Integration of a vector measure of finite variation 9.1 10A C
Integration of an infinite product 32A-D
Integration of the image of a measure 28A-C
Ionescu-Tulcea 35.1
Jessen's theorem 32.3
Joint distribution 28.15
KM 147
Kolmogoroff's theorem 30.6 see B
Lattice 14
Law of Large Numbers 33.1
Least integrable majorant 143
Lebesgue's theorem for upper gauges 8.12
Lebesgue's theorem for weak upper gauges 8.3
Lifting 34A-E 35A-C see
Lifting existence theorem 35.2
Lifting subordinate to a dense topology 34.9 see 34.14
Lifting, strong 34D 35B
Lifting, strong, vs. strong disintegration 36.6
Linear 24
Linear, purely 33
Localizable upper gauge 21C see
Localization principle 18.9
Locally almost everywhere (loc. a.e.) 140
Locally integrable functions and derivatives 22A 37B
Locally majorizable 15.9
Locally negligible 140
Locally scalarly integrable functions and derivatives 37A
Logarithmic convexity of 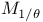 20.10 12.7 20.10 12.7
Lower semicontinuous Baire functions 6.18
Lusin space 24.8 36.5
M* 14A
Maharam 35.2
Martingale 31A-E
Martingale convergence in mean 31B 31.11
Martingale convergence in mean a.e. 31D 31.11
Martingale vs. projective limit 268
Martingale, descending 31E
Martingale, maximal martingale theorems 31C
Maximal function of a martingale 272
Maximal ideals of 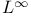 20.6 20.8 20.6 20.8
Mean 76 see
Measurability criteria 19B-C
Measurability with respect to (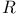 , gM) 22.4 , gM) 22.4
Measurability with respect to an image 28B-C
Measurability with respect to clans of subsets 18.20
Measurability, Baire 19.13
Measurability, Borel 19.14
Measurability, Caratheodory 19D
Measurability, scalar 19C
Measurable class 18.12
Measurable field 26A
Measurable function 18A
Measurable set 169
Measurable step function 18.10
Measurable, limit theorems see 18B
Measurable, norm- and order relations for measurable functions 21A-B
Measure see "Elementary integral" "Content" "Extension"
Measure bounded 13.12
Measure on a completely regular space 24.3
Measure space, elementary 1B 3
Measure with base and density 6.7 22C
Measure,  -bounded 13.13 -bounded 13.13
Measure, atomic (= discrete) 24B
Measure, complex 3.14
Measure, diffuse 24B
Measure, Dirac 24B
Measure, equitight family 24.14
Measure, induced on a subset 15C-D
Measure, positive 1B 3 27
Measure, Radon 1B 4 4.11
Measure, scalar, on a full integration domain 6C
Measure, tight 24A-D
Measure, variation of 3B-C
Measure,semivariation of 4C
Minkowski's inequality 12.4
Modulus 3E 36 see
Monotone convergence theorem for upper gauges 8.9
Monotone convergence theorem for weak upper gauges 8.1
Monotone convergence theorem, implies the existence of an upper integral 14.5
Morphism of integration lattices 28.18
Negligible functions and sets 7A
Negligible, locally 140
Norm relations between measurable functions 21A
Normal homomorphisms of Riesz spaces 23 see 22.3
Norming subspace 47 108
numerical see "Having values in the extended reals"
Order 12
Order complete Riesz space 17 see
Order cone 12
Order continuous form on 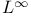 21.9 21.9
Order continuous norm 3E 36 see 9A
Order relations between measurable functions 21B
Order, dual 28 see
Ordered vector space 12
Orthogonal (= disjoint) 19
Outer gauge 9.11
Outer regular 9.12
Outer S-norm 7.23 9.11
Oxtoby 34.9
p' 192
p(m)=pm, pM 244
p-integrable functions 12B 12.8
p-norms 12A
p-norms, standard essential 141
Partition, adequate 156
Partition, refinement of 157 16.2
| Pettis integral 11A
Polish space 24.7 36.5
Positive 24
Positive element of a Riesz space 12
Positive measure or integral 27
Positively homogeneous 24
Pre-compact sets 60
Pre-compact sets are dominated 5.4 see
Pre-density 308
Pre-measure 24.3
Pro-measure 30 5
probability 33A-D
Probability space 294
Product of integrable functions 7.11 32.6
Product of measurable functions 18.5
Product of measurable maps 18.17
Product of uniformities 18.17
Products of measures or elementary integrals and martingales 32C 288
Products of measures or elementary integrals, *-continuity 27.3 32.1
Products of measures or elementary integrals, finite 27A-B
Products of measures or elementary integrals, infinite 32A
Products of measures or elementary integrals, limit theorems for 32C
Products of measures or elementary integrals, tightness 27.3
Projective sublimit 258 263
Projective system and limit of integration lattices 30A
Projective system and limit of integration lattices, epimorphic 260
Projective system and limit of integration lattices, full 260
Projective system and limit of measures or elementary integrals 30B
Projective system and limit of measures or elementary integrals, variation 30.4 31.1
Projective system and limit vs. martingales 270
Prokhorov's theorems 24.14 30.8
Proper L-space 3E 36 see
PU 28.17
Purely linear or S-continuous 33 see
Quotient of 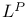 modulo M 7C 80 modulo M 7C 80
Quotient of a Riesz space by an ideal 22
R-variation 3E
R-variation of 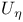 4.14 4.14
Radon measure 1B 4 4.11
Radon measure, semivariation and B-continuity of 4.11
Radon measure, variation of 4.18
Radon — Nikodym theorems for Banach-valued measures 37A-C
Radon — Nikodym theorems for scalar measures 22.6 22.7
Radonian spaces 24D
Random variable 296
Random variable independent 33C 33.4
Random variable, sequences of 33B
Rearrangement 28.15
Refinement of a partition 157 16.2
Regular Borel-measure 9.8
Regular upper gauge 19A
Relatively compact sets 5.4 see 37.7
Rickart's decomposition 17B
Riemann content 4
Riemann content, S-continuity of 34 see
Riemann integral 1A 1
Riemann integral, B-continuity of 3.18
Riesz decomposition lemma 2.14
Riesz Decomposition theorem 2.18
Riesz representation theorems 11.15 13.11
Riesz space (= vector lattice) 2B
Riesz space, complete 17
Riesz Thorin convexity theorem 23B
Ring of sets (= clan) 1B
S(f) 178
S-continuous elementary integral or measure 3D
S-continuous, purely 33
S-continuous, weakly 4D 48 see
S-measure on a full integration domain 6C
Scalarly integrable 341
Scalarly locally integrable 37A 330
Scalarly measurable 19C 306
Scalarly q-integrable 38A 341
Schwartz' tight measures 24A-D
Semivariation 4C see 104 11A 116
Solid subspace (= ideal) of a Riesz space 18
Souslin space 24.8 see
Spectrum of a clan 53
Spectrum of an integration lattice 5D
Standard essential upper integral, essential p-norm 140
Standard exhaustion argument 8.21
Standard integral extension 10A 104
Standard upper integral (gauge) for a *-measure 9A
Step function are dense 6.3 8.4
Step function on the line 1 4
Step function over a clan 1.1
Step function, measurable 18.10
Stochastic model 33A 295 33B 296
Stone Kakutani space of an upper gauge 20.12
Stone lattice 3
Stone space of an algebra 5.1
Strassen's theorem 36.8
Strictly localizable upper gauges 16A-B
Strictly localizable upper gauges are localizable 21.8
Strong dense topology 34.10
Strong disintegration 322
Strong lifting 34D
Strong upper gauge 8B 87 see
Subadditive 24
Sublattice 18
Sublinear 24
Submartingale 31A 31.3
SUG 8B 87 see III
Superadditive 24
Support of a B-measure or a B-continuous upper gauge 158 see 20.9 34D
Tame fields 25B
Tame maps 245
Thick sets 15B
Three Lines theorem 23.2
Three lines theorem, characterization 24C
Three lines theorem, form a band 24.2
Three lines theorem, images of 28C
Three lines theorem, products of 27.3
Three lines theorem, tight measures 24A
Three lines theorem, tight upper gauges 24A C
Topology admissible 108
Topology, dense 34B
Topology, dense, associated with a lifting 34.7 see 34.14
Topology, dense, strong 34.10
Tribe (=  -algebra) 6.12 -algebra) 6.12
Tribe of measruable sets 18.12
U(f) 165
U(l) 233
Ug 8B 87
Ultimately equal 291
Uniformity of dominated pointwise convergence 24.11
Uniformity of dominated uniform convergence 4B
Uniformity of uniform convergence 4.15
Uniformity on compact sets 24A
Uniformity, generated by a family of functions 5B
Uniformity, inductive limit of 4A
Uniformly absolutely continuous 120
Uniformly integrable 18.20
Universally B-measurable 215
Upper gauge 8B
Upper gauge smooth 14A
Upper gauge, essential 13A
Upper gauge, extension under an 1A 10A
Upper gauge, fields of 25A-B
Upper gauge, inner regular 9.12
Upper gauge, majorizing a linear map 104
Upper gauge, regular 19A
Upper gauge, strong 8B 87
Upper gauge, weak 8A see
Upper norms and upper S-norms 7A
Upper norms and upper S-norms, convexity properties of 12A
Vague uniformity 26A 24.13
Variation in a Riesz space 13
Variation of a Banach-valued measure 3C
Variation of a linear map 45
|
 |
|
О проекте
|
|
О проекте



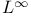
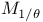
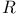 , gM)
, gM)  -bounded
-bounded 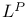 modulo M
modulo M