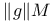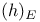 111 111
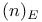 31 31
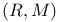 83 83
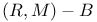 -adequate fields 234 -adequate fields 234
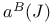 19.14 19.14
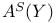 19.13 19.13
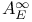 256 256
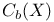 213 213
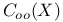 4 4
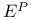 253 253
![$E^X[M]$](/math_tex/4db5b5c626607f6c2ab17ecee52931db82.gif) 75 75
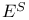 29.8 29.8
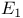 , , 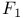 , , 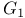 48 48
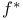 , , 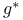 74 74
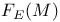 , F(M) 78 , F(M) 78
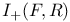 , , 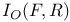 27 27
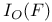 28 28
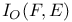 30 30
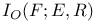 37 37
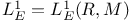 80 80
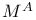 , , 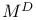 , , 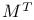 210 212 210 212
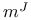 2 7.16 2 7.16
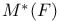 32 32
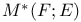 33 33
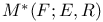 37 37
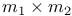 238—240 238—240
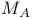 , , 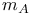 151 151
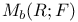 13.12 13.12
 133 133
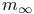 261 261
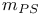 , , 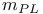 33 17B 33 17B
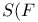 , , 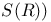 57 57
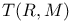 173 173
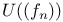 167 167
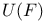 52 52
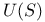 233 233
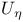 , , 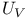 49 116 49 116
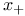 13 13
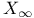 , , 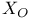 57 57
![$[h]_E$](/math_tex/2858987c2621e71d89d0ef35952f9a9982.gif) 120 120
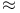 8.18 8.18
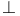 19 31 19 31
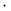 , , 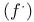 74 74
 56 56
 51 51
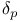 , , 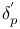 239 239
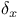 210 210
 , , 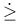 (M) 74 (M) 74
 54 56 54 56
 , ,  12 12
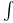 104 114 104 114
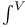 117 117
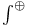 82 82
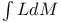 226 226
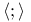 223 225 223 225
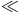 21 31 38 7.20 9.9 21 31 38 7.20 9.9
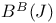 19.14 19.14
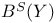 19.13 19.13
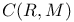 85 85
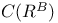 92 92
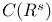 66 66
![$\mathscr{D}_E[\mathscr{R}]$](/math_tex/cacbf323ea1341dadbf5d11eefe997b482.gif) 41 41
 302 302
 303 303
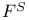 65 65
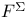 72 72
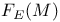 , , 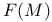 76 76
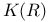 , , 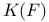 41 41
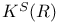 , , 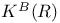 , , 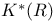 64 64
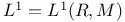 78 78
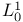 8.19 8.19
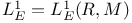 78 78
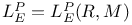 136 136
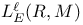 , , 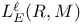 198 198
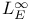 , , 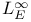 185 185
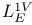 117 117
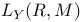 165 165
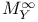 306 306
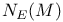 , , 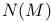 78 78
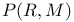 156 156
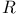 -topology 5.11 -topology 5.11
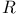 -topology, vague 24.13 -topology, vague 24.13
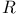 -uniformity 5B -uniformity 5B
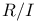 22 22
![$\mathscr{R}[K]$](/math_tex/edd3588f50baba8bdfcd8ec84ad3487582.gif) 42 42
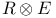 42 42
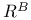 , , 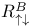 92 92
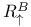 , , 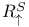 , , 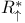 , , 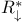 64 90 64 90
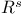 , , 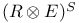 66 66
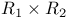 237 237
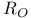 42 42
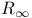 259 259
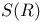 1 1
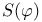 5 5
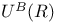 , , 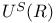 , , 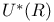 64 64
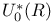 9.6 9.6
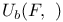 53 53
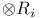 285 285
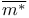 , , 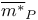 141 141
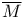 138 138
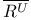 5.3 58 5.3 58
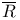 , , 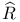 59 59
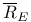 43 59 61 43 59 61
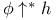 32 32
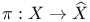 54 57 54 57
 -additive content 34 -additive content 34
 -algebra (= tribe) 6.12 -algebra (= tribe) 6.12
 -bounded measures 13.13 -bounded measures 13.13
 -closure 6.16 -closure 6.16
 -finite sets and upper gauges 13A 138 -finite sets and upper gauges 13A 138
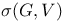 47 47
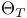 305 305
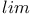 258 261 270 258 261 270
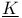 158 158
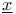 158 158
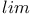 40 40
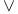 , , 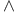 14 14
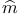 17A 17A
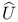 62 62
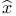 54 54
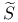 56 56
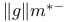 22.8 22.8
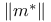 9.1 9.1
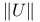 , |U| 45 , |U| 45
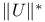 116 11.8 116 11.8
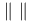 45 45
' 47
(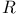 , , 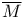 ) 138 ) 138
(A),(n),(x) 18
*-continuity 3D 31
*-continuity is determined on a uniformly dense subspace 3.15
*-continuity of a product 27.3 32.1
*-continuity of an integral of a field 25.4
*-continuity, weak 4D
*-continuous elementary integrals 3D see
*-continuous, measures 3D 31 see
1 48
A(P) 247
Absolute continuity for Banach-valued measures 31
Absolute continuity for upper S-norms 7.20 see 15.8
Absolute continuity in a Riesz space 21
Absolute continuity, characterization for scalar measures 3.8 6.7 see 29A
Absolute continuity, uniform absolute continuity of linear maps on a convex set 119—120
Absolute value 13
Adapted maps 28B
Adequate cover by integrable sets 86 see
Adequate cover by measurable sets 170
Adequate field 26B
Adequate map 28A
Adequate partition 16A 156
| Admissible function 252
Admissible topology 108
Algebra of sets 6 11
Almost compact measures 37A
Almost compact-valued functions 178
Almost everywhere (a.e.) 74
Almost separably-valued functions 178
AM 147
AU 153
B-continuous integral of a field 26A-B
B-continuous measure (= B-measure) 3D see 4.19
B-continuous part of a measure 3 11 17 3
B-continuous upper gauge 8C see 11.8
B-continuous upper gauge, associated with a lifting 34.1
B-continuous, weakly B-continuous linear maps 4D 11A 116
Baire category theorem 11.5
Baire functions and sets 6.16
Baire functions and sets, dominated 66 8.23
Baire functions and sets, equivalent to an integrable function 7.18
Baire measurable functions 19.13
Banach lattice 3E 36 see 10
Banach lattice with order-continuous norm 3E 36 see 9A 94
Banach space over a Banach lattice 3E 36 see
Band 18
Band decomposition of Riesz 2.18 see
Band of *-measures 3.10 3.11 3E
Band of diffuse, discrete, or tight measures 24C
Band, a band in a band is a band 2 24
Band, characterizations 2.20 2.21
Bauer's theory 17A see 10.7 24.1
Bochner integrable 78
Bochner integral 10A
Bochner integral of a weakly compact linear map 11C see
Borel functions and sets 18.21
Borel functions and sets, dominated 92 8.23
Borel measurability 19.14
Borel — Cantelli lemma 32.5
C(f) 178
C(n), C(n,M) 330
Caratheodory 19.D
ce(), 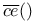 107 107
Chain rule 22.9
Character (space) of 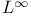 20B see 20B see
Character (space) of a family of functions 54
Clan (= ring of sets) 1B 5 see 6.1 "Full" "Extension" "Spectrum"
Clan of integrable sets 8.4
co(), 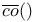 106 106
Compact and 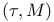 -compact linear maps 10B -compact linear maps 10B
Compactness criterion for admissible topologies 10.6
Compactness of 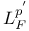 21.11 21.11
Compactness properties of the integral 10B
Completeness of 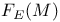 7.9 7.9
Completeness of 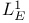 7.12 7.12
Completeness of 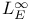 20.3 20.3
Completeness of a Riesz space 17
Complex measures 3.14
Conditional distribution 36.10
Conditional expectation 29A-C
Conditional expectation under 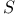 29.8 29.8
Conjugate numbers 193
Content, elementary 1B 5
Content, elementary, extension 1.1 3.12 98
Content, elementary, S-continuous (=  -additive) 34 -additive) 34
Continuity a.e. with respect to a lifting 34.8
Continuity of linear maps on 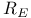 4.6 4.6
Convergence a.e. 74
Convergence at infinity 54
Convergence in mean 76
Convergence in measure 18.14 28.15
Convergence of a martingale 31A-D
Convergence of a martingale, locally in p-mean 31.2 31.11
Convergence of a martingale, pointwise 31D 31.11
Daniell integration 1A
Daniell integration, of linear maps 11C
Darboux property 24.12
Dense family of integrable sets 86
Dense family of integrable sets, examples 8.8 8.20 165
Dense subsets of  8.4 8.4
Dense topology 34B see
Dense, 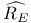 in in 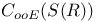 5.3 5.3
density 34.11 see
Derivative, locally integrable 22A-B
Derivative, locally integrable, existence for almost weakly compact measures 37B
Derivative, locally integrable, existence for scalar measures 22.6 22.7
Derivative, scalarly locally integrable 37A
Dini's theorem 4 12
Dirac measure 24B
Direct integral of Banach spaces 7.22
Direct sum of Riesz spaces 20
Direct sum property 16.10
Discrete (= atomic) measures 210
Disintegration of a measure 36A
Disintegration of a support function 36.8
Disintegration of a tight measure 36.3
Disintegration, strong 36.3 see
Disjoint Banach-valued measures 3C 31 3.17
Disjoint elements of a Riesz space 19
Disjoint, characterization of disjoint scalar measures 3.8 6.6
distribution 28.15
dm/dn 198
Dominated Baire functions and sets 66
Dominated Borel functions and sets 92
Dominated functions and sets 4B
Dominated integration lattices 4.4
Dominated sets are precompact 5.4
Doob's martingale theorem 31.9
Dual of  21.6 21.7 31.7 21.6 21.7 31.7
Dual of 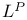 21.7 37.1 21.7 37.1
Dual of a Riesz space 28
E', F', G' 47
Egoroff's theorem 18.11
Elementary integral 1B 3
Elementary integral, *-continuous 3D 31
Elementary integral, associated with an elementary content 1.1 3.12
Elementary measure space 1B 3
Elementary measure space, *-continuous 31
Equi-tight measures 24.14
Equivalent functions modulo negligible ones 78
Equivalent upper gauges 8.18 see
Equivalent upper gauges are simultaneously tight 24.16
Equivalent upper gauges have the same dense dominated families 14.4
Equivalent upper gauges have the same essential sup-norm 20.2
Essential  -open kernel 34.11 -open kernel 34.11
Essential essentially equal upper S-norms 7.15
Essential supremum norm 20A
Essential upper gauge 13A
Expectation 33A see
Extended reals 5A
Extension of an elementary content on a clan 1.1 3.12 98
Extension of an elementary integral under an upper norm 1A 10A
Extension of linear maps 11A 11C
Extension of the Riemann integral of step functions 1A
Fatou's lemma 8.11
Field of integrable variation 218
Field of linear maps 224
Field of measures and of upper gauges 25A-B 26A-C see
Field, adequate 26A-B
Field, integrable 25A
Field, tame 230
Finite sets and upper gauges 13A 138
Fubini's theorem 25.3 see 27.4 36.4
Full clan (= -ring) 66 67 -ring) 66 67
Full integration domain 6B see 6C "S-measure"
Full projective system or limit 30A
Full span 6A
Gelfand transform of functions 5D
Gelfand — Bauer transform of measures 5D 17A-B see
gM, 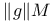 199 15.9 199 15.9
gm, gn 70 197
Hahn's theorem 6.6 see 6.17
|
 |
|
О проекте
|
|
О проекте



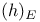
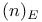
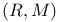
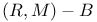 -adequate fields
-adequate fields 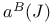
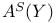
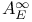
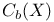
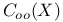
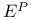
![$E^X[M]$](/math_tex/4db5b5c626607f6c2ab17ecee52931db82.gif)
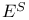
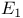 ,
, 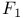 ,
, 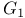
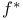 ,
, 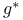
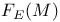 , F(M)
, F(M) 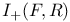 ,
, 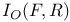
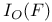
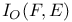
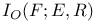
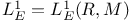
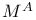 ,
, 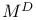 ,
, 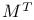
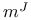
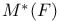
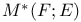
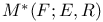
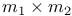
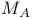 ,
, 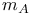
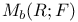

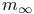
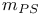 ,
, 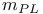
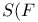 ,
, 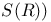
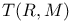
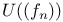
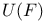
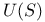
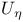 ,
, 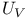
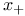
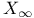 ,
, 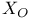
![$[h]_E$](/math_tex/2858987c2621e71d89d0ef35952f9a9982.gif)
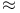
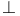
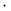 ,
, 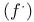


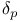 ,
, 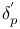
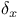
 ,
, 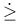 (M)
(M) 
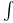
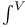
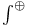
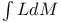
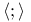
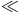
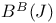
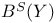
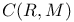
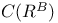
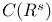
![$\mathscr{D}_E[\mathscr{R}]$](/math_tex/cacbf323ea1341dadbf5d11eefe997b482.gif)
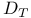
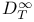
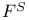
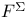
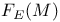 ,
, 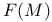
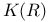 ,
, 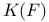
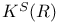 ,
, 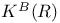 ,
, 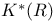
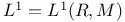
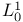
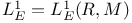
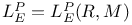
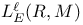 ,
, 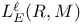
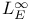 ,
, 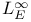
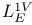
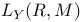
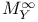
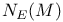 ,
, 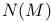
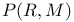
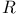 -topology
-topology 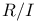
![$\mathscr{R}[K]$](/math_tex/edd3588f50baba8bdfcd8ec84ad3487582.gif)
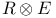
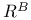 ,
, 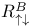
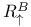 ,
, 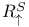 ,
, 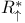 ,
, 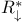
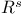 ,
, 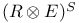
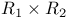
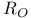
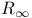
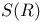
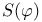
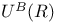 ,
,  ,
, 
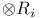
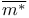 ,
, 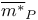
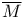
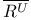
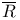 ,
, 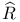
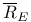
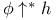
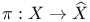
 -additive content
-additive content  -closure
-closure 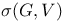
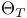
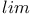
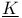
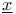
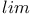
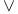 ,
, 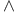
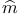
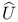
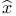
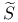
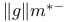
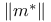
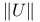 , |U|
, |U| 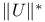
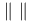
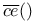
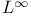
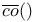
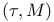 -compact linear maps
-compact linear maps 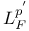
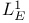
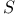
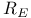

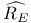 in
in 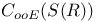

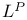
 -open kernel
-open kernel  -ring)
-ring)