|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bishop Y.M.M., Feinberg S.E., Holland P.W. — Discrete Multivariate Analysis, Theory and Practice |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Hartley, H.O. 439 539
Hedayat, A. 215 534
Henry, N.W. 344 537
Hierarchy of models 320—324
Hierarchy principle 33 38 67—68
Hilferty, M.M 527 541
Hitchcock, S.E. 358 536
Hoel, P.G 270 536
Hogg, R.V 65 536
Holland, P.W. 370 404 405 407 412 413 414 416 417 418 422 423 429 433 493 518 534 536 541
Homeogeneity, marginal 54—55 282
Homeogeneity, of proportions 347
Homeogeneity, test for 293—296 306—309
Homogeneous Markov chain 262
Hypergeometric distribution, multivariate 450—452
Hypergeometric distribution, univariate 488—450 (see also “Exact theory”)
Incomplete arrays, for subsets of complete arrays 111 206—210 225—228
Incomplete arrays, multiway 210—225
Incomplete arrays, square tables and 283 290
Incomplete arrays, triangular 31
Incomplete arrays, two-way 178—206
Independence, as lack of association 374—380
Independence, in rectangular array 28—29
Independence, in three-way array 3 8
Independence, quasi 178—182 287—293
Independence, surface of 51
Indirect estimates see “Fitting iterative “Partitioning
Information theory, minimum discrimination information (MDI) 344—347
Information theory, model generation 345—346
Information theory, modified MDI (MMDI) 295—296 347
Interaction, assessing magnitude of 146—155
Interaction, test for 146—155 364—366
Ireland, C.T. 85 284 295 296 345 346 347 348 536
Irregular arrays 21 48 (see
Isolates 193
Iterative proportional fitting 83—102 188—191
Iterative scaling see “Iterative proportional fitting”
Jackknifmg 319
Jackson, P.H. 403 539
James, W. 403 536
Johnson, B.M. 407 536
Johnson, N.L 435 438 439 456 536
Johnson, W.D 143 353 536
Jones, R. 196 221 222
Joshii, S.W 435 539
Judge, G.G. 261 537
K, sum of Dirichlet parameters 401—402 405—408 420—426 K”)
Kalton, G 132 537
Kannel, W.B 358 359 360 533 541
Kastenbaum.M.A. 84 178 200 537 540
Katz, L. 277 278 279 537
Kemeny, J. 312 537
Keyfitz, N. 247 533
Kitagawa, E.M. 132 537
Kleinman, J.C 344 370 537
Koch, G G 143 284 306 308 353 354 532 536 537
Kondo, T 519 537
Korff, F.A 90 537
Kotz, S. 435 438 439 456 536
Kruskal, J.B 298 537
Kruskal, W.H 373 374 375 376 380 387 388 389 391 393 502 535 536 537
Ku, H.H. 127 143 148 284 295 296 344 346 347 348 363 536 537
Kucera, H. 331 537
Kulkarni, S.R 370 531
Kullback — Liebler distance 345 (see also “Information theory” “Likelihood
Kullback, S. 85 127 143 148 284 295 296 299 306 344 345 346 347 348 363 536 537
Kupperman, M. 127 363 537
Lambda, as measure of association 388—389
Lambda, as weight for Dirichlet prior 405—406 419—426 429—433
Lancaster, H.O. 1 2 244 261 262 262 522
Larntz, K. 205 522
Larzarsfeld, P.F. 256 265 225 344 532
Latent structure analysis 344
Lauh, E. 142 522
Least squares, weighted 352—357
Lee, T.C. 261 353 522 542
Lehman, E. 265 463 522 522
Lemon, R.E. 225 532
Leonard, T. 403 404 422
Levine, J.H. 100 101 532
Lewis, C. 402 522
Li, C.C 242 532
Lieberman, G. 449 522
Light, R.J. 224 220 221 226 222 400 523
Likelihood ratio statistic,  125—130 125—130
Likelihood ratio statistic,  , asymptotic distribution of 513—516 , asymptotic distribution of 513—516
Likelihood ratio statistic,  , calculus for partitioning 169—175 , calculus for partitioning 169—175
Likelihood ratio statistic,  , compared with Pearson’s chi-square 125—126 , compared with Pearson’s chi-square 125—126
Likelihood ratio statistic,  , conditional breakdown of 126—127 , conditional breakdown of 126—127
Likelihood ratio statistic,  , conditional test for marginal homogeneity 293—294 307 , conditional test for marginal homogeneity 293—294 307
Likelihood ratio statistic,  , definition of 58 , definition of 58
Likelihood ratio statistic,  , for direct models 129—130 158—160 , for direct models 129—130 158—160
Likelihood ratio statistic,  , for incomplete tables 191 , for incomplete tables 191
Likelihood ratio statistic,  , for indirect models, bounds for 160—161 , for indirect models, bounds for 160—161
Likelihood ratio statistic,  , for symmetry 283 , for symmetry 283
Likelihood ratio statistic,  , structural breakdown of 127—130 , structural breakdown of 127—130
Lin, Y.S 400 528
Lincoln, F.C. 233 538
Lindley, D.V. 402 538
Lindon, J.A. 340
Linear contrast, asymptotic variance of 494—497
Linear contrast, interpretations of 15 16 26—27 181 211—222 “u-terms”)
Linear models see “Additive models”
Loeve, M. 463 464 462 538
Log-linear model, for 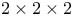 table 32—33 table 32—33
Log-linear model, for 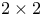 table 16—17 179 table 16—17 179
Log-linear model, for 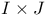 table 24—26 179 table 24—26 179
Log-linear model, for 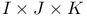 table 35—41 table 35—41
Log-linear model, for 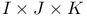 table, interpretation of 37—39 table, interpretation of 37—39
Log-linear model, general 42—47
Log-linear model, general, interpretation of 45—47
Log-linear model, random effects models 371
Log-linear model, with terms of uniform order 119—121 156—158 “Cross “Direct
Logistic response function, multivariate 360
Logistic response function, univariate 357—360 (see also “Logit model”)
Logit model, alternatives to 367—371
Logit model, continuous variable 358
Logit model, definition of 22—23
Logit model, discrete variable 3 5 7—3 61
Logit model, for 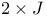 table 30 table 30
Logit model, minimum chi square for 355—357
Logit model, mixed variable 358
Loglinear contrasts see “Linear contrast”
Loops, closed 76
Lowe, C.R. 102 102 523
Lyell, L.P. 358 533
MacMahon, B. 102 103 538
MacWilliams, H.K. 152 153 533
Madansky, A. 260 261 294 295 301 306 307 538
Mantel — Haenszel test 133 147—148 151
Mantel, N. 124 146 173 193 194 197 247 255 366 531 537 538
Marginal homogeneity see “Homogeneity”
Margins, lines of constant 53
Margins, measures insensitive to 392—393 (see also “Cell values” “Configuration”)
Margolin, B.H. 374 390 391 538
Markov models, assessing order of 269—270
Markov models, assessing order of, for aggregate data 260—261
Markov models, for cross classified states 273—279
Markov models, for different strata 277—279
Markov models, higher order 267—270
Markov models, single sequence transitions of 270—273
Markov models, time-homogeneity 261—267 269
Marx, T.J. 400 538
Maximum entropy 345—346 (see also “Information theory”)
Maximum likelihood estimates (MLEs), advantages of 58
Maximum likelihood estimates (MLEs), asymptotic behavior of 509—513
Maximum likelihood estimates (MLEs), conditional for closed populations 237—238
Maximum likelihood estimates (MLEs), existence of, for incomplete tables 186 216
Maximum likelihood estimates (MLEs), expansion of, for multinomial 511—513
Maximum likelihood estimates (MLEs), for marginal homogeneity 294—295 306
| Maximum likelihood estimates (MLEs), for Markov chain transition probabilities 262—263 267—268
Maximum likelihood estimates (MLEs), for quasi-symmetry 289 306—319
Maximum likelihood estimates (MLEs), for symmetry 283 301—302
Maximum likelihood estimates (MLEs), methods of obtaining 73—83
Maximum likelihood estimates (MLEs), relative precision of 313—315
Maximum likelihood estimates (MLEs), suitability for likelihood ratio statistic 125—126
Maximum likelihood estimates (MLEs), uniqueness of, in incomplete tables 185
Maximum likelihood estimates (MLEs), when model is incorrect 513 (see also “Fitting Iterative proportional” “Birch’s “Direct
Maxwell, A. 1 538
Mayhall, J.T. 333 539
McNemar test 258 285
McNemar, Q. 258 285 309
MDI see “Information theory”
Mendel, G 312 327 328 329 538
Menzerath, P. 272 538
mgf see “Moment generating function”
Miller, G.A. 261 538
Minimax estimates 407
Minimum distance measure, asymptotic variance of 518—519
Minimum distance measure, methods 504—505 (see also “Pearson’s chi square” Neyman’s “Minimum
Minimum logit 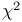 355—357 355—357
Mitra, S.K 518 538
MLE see “Maximum likelihood estimates”
MMDI see “Information theory”
Model, selection of 155—168
Model, simplicity in building a 312—313 (see also “Log-linear model” “Additive
Molina, E.C. 439 538
Moloney, W.C. 124 125 148 540
Moment generating function, to show convergence 469 (see also “Sampling distribution”)
Moments, limits of 485
Moments, methods of 505—507
Moments, order of 485—486 (see also “Binomial distribution moments “Hypergeometric “Multinomial “Poisson
Morgan, J.N. 360 540
Morris, C. 403 410 442 534 538
Morrison, A.S. 102 103 538
Mosteller, F. 15 100 101 105 106 134 135 136 260 262 316 317 318 319 327 331 332 337 368 375 401 436 492 532 538 539
Muller, T.P 333 539
Multinomial distribution, asymptotic normality of 469—472
Multinomial distribution, asymptotic variance of loglinear contrasts for 494—497
Multinomial distribution, estimation for 504—505
Multinomial distribution, formal stochastic structure for 480—481
Multinomial distribution, general theory for estimating and testing with a 502—508
Multinomial distribution, goodness-of-fit tests 507—508
Multinomial distribution, negative multinomial 454—456
Multinomial distribution, product multinomial 61 70—71
Multinomial distribution, sampling distribution 61 441—446
Multinomial distribution, variance of log-linear contrasts 494—497
Multiplicative models 225—228 320—324
Multiplicative models, estimating the mean of 403
Multivariate normal distribution, asymptotic distribution for multinomial 469—472
Murthy, V.K 524 539
Myerowitz, R.L. 124 125 148 540
Nerlove, M 360 539
Nested models, difference in  524—526 (see also “Likelihood ratio statistic 524—526 (see also “Likelihood ratio statistic
Newman, E.B. 270 271 272 273 539
Neyman, J. 58 349 351 454 539
Neyman’s chi square, minimizing 349—350
Neyman’s chi square, with linear constraints 351—352
Neyman’s chi square, with linear constraints, equivalence to weighted least squares 352—354
Noninteractive cell 181—182 193—194
Normal approximations to the binomial 464—465
Norming measures of association 375—376
Notation for models, dimension-free 61—62 (see also “O o
Novick, M.R 403 539
Novitski, E. 200 201 202 205 539
O, o notation, Chernoff — Pratt 479—480 481
O, o notation, conventions in use of 459—460
O, o notation, definitions 458—459 460
O, o notation, generalized for stochastic sequences 475—484
O, o notation, related to order of moments 485—486
Occurrence in probability 482—484
Odoroff, C.L. 140 539
Olson, N.C. 489 539
Oslick, A. 99 531
Outliers 140—141
Owen, D.B 439 449 537 539
P see “Pearson’s measures of association”
Panel studies 257—260 265—267
Parameters see “u-terms”
Partial association models, degrees of freedom for 121—122
Partial association models, fitting 161—165
Partitioning chi square 524—526
Partitioning chi square, calculus of Goodman 169—175
Partitioning chi square, Lancaster’s method 361—364
Partitioning chi square, likelihood ratio statistic 524—526
Pasternack, B. 116 117 118 541
Patil, G.P. 435 539
Pdf (probability density function) 63
Pearson, E.S. 439 539
Pearson, K 339 382 385 423 425 539
Pearson’s chi square, asymptotic distribution of 472—474
Pearson’s chi square, asymptotic relation to other statistics 513—516
Pearson’s chi square, compared with  124—125 124—125
Pearson’s chi square, correction for continuity 124 258
Pearson’s chi square, definition of 57
Pearson’s chi square, incomplete tables 191
Pearson’s chi square, large samples and 329—332
Pearson’s chi square, limiting distribution of, for complex cases 520—522
Pearson’s chi square, limiting distribution of, for complex cases, under alternative 329—332 518
Pearson’s chi square, limiting distribution of, for complex cases, under null model 516—518
Pearson’s chi square, minimizing 348—349
Pearson’s chi square, noncentral distribution 473—474 518
Pearson’s measures of association, 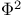 330 385—387 330 385—387
Pearson’s measures of association, P 382—383 385—387
Peizer, D.B. 457 539
Percentage points, for x distribution 527—529
Petersen, C.G.J. 232 539
Pfaffinan, C. 220 221 534
Pincus, G.S. 124 125 148 540
Plackett, R.L 15 124 353 365 366 375 539
Ploog, D.W. 203 539
Poisson distribution, asymptotic distribution of powers of mean 489—490
Poisson distribution, relationship to multinomial 440—441 446—448
Poisson distribution, sampling distribution 62 185—186 438—441 446—448
Poisson distribution, truncated variates 503—504 506 607 521—522 523—524
Poisson distribution, variance-stabilizing transform for 492 (see also “Frequency of frequencies” “Hansen “Maximum “Sampling
Pool, I. 107
Population-size estimation 229—256
Poskanzer, D. 196 221 222
Pratt, J. 457 475 480 481 483 539 540
Pratt, occurrence in probability 482—484 (see also “Stochastic sequence” “Notation dimension-free”)
PRE (proportional reduction in error) 387—389
PRECISION 313—315 (see also “Variance”)
Press, S.J. 360 539
Prince, T. 362
Probit transformation 367
Proctor, C.H. 277 278 279 537
Propagation of errors see “Delta method”
Pseudo-Bayes estimators 408—410 419—423
Pseudo-Bayes estimators, asymptotic results for 410—416
Pseudo-Bayes estimators, small sample results for 416—419
PV (predictive value) 21—22
q see “Association measures “Cochran’s “Yule’s
Quasi-independence see “Independence”
Quasi-loglinear 210—212
Quasi-perfect mobility 206—208
Quasi-symmetry see “Symmetry”
Rabinowitz, P. 410 533
Rao, C.R 58 472 473 474 505 525 540
Rasch, G. 344 540
Ratcliff, D 85 289 533
Rates, adjusting for multiple variables 123 133—136
Rates, direct standardization 131—132
Rates, generic form 133—136
Rates, indirect standardization 132
Rates, standard mortality ratio 132 135
Rearranging data, breaking apart an 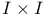 table 207—209 table 207—209
Rearranging data, fitting by stages 107—108
Rearranging data, in 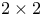 table 11—16 table 11—16
Rearranging data, partitioning 105—107
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå




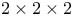 table
table 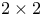 table
table 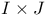 table
table 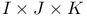 table
table 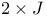 table
table 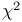
 table
table