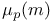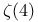|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Boros G., Moll V. — Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals |
|
|
 |
| Предметный указатель |
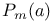 , coefficients 208 , coefficients 208
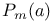 , definition 139 , definition 139
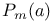 , hypergeometric representation 155 , hypergeometric representation 155
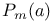 , recurrence 148 , recurrence 148
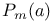 , single sum 155 , single sum 155
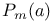 , triple sum 143 , triple sum 143
 , definition 106 , definition 106
 , irrationality 117 , irrationality 117
 , Wallis' product representation 128 , Wallis' product representation 128
 , websites 111 , websites 111
Abel, N., unsolvabiiity of the quintic 43
Adamchik, V., expressions for Catalan's constant 109
Adamchik, V., logarithmic integrals 237—238
Adamchik, V., negapolygamma function 215
Addison, A.W., series representation for  183 183
Advanced functions, Beta: B, definition 192
Advanced functions, Beta: B, functional equation 192
Advanced functions, Beta: B, integral representation 193
Advanced functions, Beta: B, trigonometric integrals 194
Advanced functions, Cosine integral: ci 136
Advanced functions, Dilogarithm: Dilog(x), definition 62
Advanced functions, Dilogarithm: special values 245
Advanced functions, Exponential integral: Explntegral(at x) 98 104
Advanced functions, Gamma:  , definition 186 , definition 186
Advanced functions, Gamma:  , Euler's definition 188 , Euler's definition 188
Advanced functions, Gamma:  , evaluation of sums 23 , evaluation of sums 23
Advanced functions, Gamma:  , functional equation 187 , functional equation 187
Advanced functions, Gamma:  , Gauss's multiplicative formula 205 , Gauss's multiplicative formula 205
Advanced functions, Gamma:  , Holder's theorem 210 , Holder's theorem 210
Advanced functions, Gamma:  , infinite product 204 , infinite product 204
Advanced functions, Gamma:  , integral representation 193 , integral representation 193
Advanced functions, Gamma:  , Legendre's duplication formula 195 , Legendre's duplication formula 195
Advanced functions, Gamma:  , reflection rule 189 , reflection rule 189
Advanced functions, Gamma:  , relation to Euler's constant 190 , relation to Euler's constant 190
Advanced functions, Gamma:  , relation to normal integral 166 , relation to normal integral 166
Advanced functions, Hurwilz zeta: 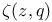 215 248 215 248
Advanced functions, Hypergeometric: ![$_2 F_1[a, b , c; x]$](/math_tex/44d87f1cfa27f4d991829f11bb7d99e082.gif) arctangent 109 arctangent 109
Advanced functions, Hypergeometric: logarithm 75
Advanced functions, Hypergeometric: polynomials 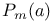 155 155
Advanced functions, Hypergeometric: relation to arcsine 122
Advanced functions, Hypergeometric: series evaluation 59
Advanced functions, Hypergeometric: symbolic evaluation 54
Advanced functions, Logarithmic integral, delinition 98
Advanced functions, Logarithmic integral, relation to prime numbers 220
Advanced functions, Loggamma function, definition 201
Advanced functions, Loggamma function, integrals 203
Advanced functions, Loggamma function, Taylor series 201
Advanced functions, Poly gamma, definition 214
Advanced functions, Poly gamma, logarithmic integrals 264
Advanced functions, Poly Logarithm, definition 239
Advanced functions, Poly Logarithm, logarithmic integrals 245
Advanced functions, Psi:  , definition 212 , definition 212
Advanced functions, Psi:  , integral representation 215—217 , integral representation 215—217
Advanced functions, Psi:  , series expansion at 0 213 , series expansion at 0 213
Advanced functions, Psi:  , special values 212 213 , special values 212 213
Advanced functions, Sine integral: si 136
Algebraic functions, definition 79
Algebraic functions, double square root 80
Algebraic functions, lnx is not one 80
Algebraic numbers, definition 80
Almkvist, G., generating function for 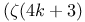 236 236
Alzer, H., arithmetic-geometric mean inequality 88
Alzer, H., bounds on harmonic mean of 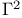 191 191
Alzer, H., optimal growth for Bernoulli numbers 102
Alzer, H., sequences related to harmonic numbers 175
Amdeberham, T., iterative primitives of In x 82
Amdeberham, T., series for 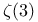 236 236
Andrews, G., Death of Proof? 271
Apery's number, Amdeberham's formula 236
Apery's number, Beukers' formula 234
Apery's number, definition 231
Apery's number, eslimates of Euler's constant 175
Apery's number, Ewell's formula 232
Apery's number, integral representation 232
Apery's number, integral with arcsine 122
Apery's number, irrationality 232
Apery's number, Sondow's antisymmetric formula 234
Apery's number, Yue and William's formula 233
Apostol, T., Dirichlet series 224
Apostol, T., Euler — MacLaurin summation 94
Apostol, T., proof of 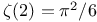 225 225
Apostol, T., proof of von Staudt — CIausen theorem 101
Arcsine function, definition 107
Arcsine function, power series 119
Arcsine function, power series of the cube 123
Arcsine function, power series of the square 122
Arctangent function, definition 19 107
Arctangent function, hypergeomelric representation 109
Arctangent function, polynomial approximation 124
Arctangent function, power series 109
Arctangent function, relation to Arcsine 107
Arithmetic geometric mean 88
Arora, A.K., logarithmic integral 241
Arora, A.K., logsine integral 245
Artin, E., conjecture on primitive roots 134
Ascending factorial symbol, definition 16
Ascending factorial symbol, dimidiation formula 17
Ascending factorial symbol, duplication formula 17
Ascending factorial symbol, extended binomial coefficients 65
Ascending factorial symbol, relation to  187 187
Ascending factorial symbol, Vandermonde's formula 18
Assmus, E.F.,  in length and area of a circle 108 in length and area of a circle 108
Atkinson. M.D., series for tan* and sec x 133
Ayoub. R., nonsolvabilily of polynomials 43
Barnes, C W., e as a limit 85
Barnes, C W., existence of Euler's constant 174
Bateman, manuscript project 55
Beatly, S., e is not a quadratic irrational 90
Berndt, B., Entry 21 of Chapter 26 in Ramanujan's Notebook 178
Berndt, B., history of Lagrange's inversion formula 150
Berndt, B., integral for Euler's constant 180
Berndt, B., optimal bounds on 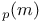 145 145
Berndt, B., unpublished notes on  187 187
Bernoulli numbers, definition 99
Bernoulli numbers, denominators 101
Bernoulli numbers, expansion of cosecant 132
Bernoulli numbers, expansion of cotangent 130
Bernoulli numbers, expansion of tangent 132
Bernoulli numbers, integral representation 223
Bernoulli numbers, optimal growth 102
Bernoulli numbers, relation to the  function 131 function 131
Bernoulli numbers, relation to the Euler numbers 132
Bernoulli numbers, sign 101
Bernoulli numbers, von Staudt — CIausen 101
Bernoulli polynomials 101—102
Bertrand's postulate 77
beta function see Advanced functions. Beta
Beukers, F., formula for 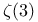 234 234
Beukers, F., integrals and coninued fractions of  126 126
Beukers, F., triple integral for 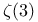 232 232
Beumer, M.G., recursion for logsine integrals 246
Bharghava, S., optimal bounds on 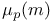 145 145
Binomial coefficients 10
Binomial recurrence 11
Binomial theorem 10
Binomial, central 14 66 94 256
Binomial, extended 65
Biquadratic integral, elementary evaluation 44
Biquadratic integral, explicit value 156
Biquadratic integral, relation to the polynomial 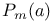 139 139
Biquadratic integral, Taylor expansion of double square root 150
Blind evaluation 20
Blyth, C., proof of Stirling's formula 92
Boas, R., partial sums of harmonic series 78
Bohr — Mollerup theorem 187
Boruein. J. and P., arithmetic-geometric mean 88
Boruein. J. and P., calculation of  185 185
Boruein. J. and P., elliptic integrals 110
Boruein. J. and P., evaluation of normal integral 164
Boruein. J. and P., integral for 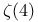 235 235
| Boruein. J. and P., series for 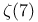 235 235
Bowman, D., integral for Euler's constant 180
Bradley, D., divergence of harmonic series 78
Bradley, D., formulas for Catalan's constant 109
Bradley, D., series for 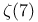 235 235
Brenner, J.L., sequences related to harmonic numbers 175
Brent, R.P., calculation of  184 184
Brenti, F., logconcavity criteria 157
Breusch, R., proof of irrationality of  117 117
Bromwich, T.J., double square root series 151
Bromwich, T.J., zeta series 214
Bronstein, M., indefinite integration 147
Brown, J.W., relation between B and  192 192
Calabi, E., proof of 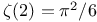 226 226
Calculus, Fundamental Theorem of Calculus 19
Calculus, primitive 19
Cardano, G., solution of the cubic equation 39
Cardano, G., solution of the quartic equation 42
Carlitz, L., logconcavity and reciprocal of series 158
Catalan's constant, Adamchik's expressions 109
Catalan's constant, Bradley's expressions 109
Catalan's constant, definition 109 221
Catalan, E., formula for  179 179
Cauchy, A., product of power series 66
Chebyshev, P.L., polynomials of the first kind 110
Chen, C.P., best bound on harmonic sequence 181
Chernhoff, P., special zeta series 248
Choe, B.R., proof of 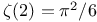 230 230
Choi, J. 203
Chong, K., proof of arithmetic-geometric mean inequality 88
Coleman, A.J., evaluation of the normal integral 169
Coolidge, J., information about c 85
Cotangent, definition 129
Cotangent, expansion at 0 130
Cox, D. et al. 160
Danese, A., a zeta series 248
Davis, P.J., Euler and history of the gamma function 187
Debnath, L., inequalities involving e 86
Derangment numbers, closed form 2
Derangment numbers, definition 2
Desbrow, D., proof of irrationality of 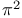 117 117
Descartes, R., solution of the quartic equation 42
DeTemple. D., fast convergence to  181 181
Dilcher, K., website on Bernoulli numbers 99
Dilogarithm see Advanced functions Dilogarithm
Dirichlet series 224 246
Discriminant curve 41
Discriminant of a cubic 39
Discriminant of a quadratic 31
Doetsch, G. 55
Dunham. W., biography of Euler 187
e, definition 84
e, irrationality 89
e, limit form 85
e, series form 85
EKHAD, automatic proofs 273
Elkies, N., story of Calabi's proof of 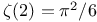 226 226
Elkies, N., zeta series 221
Elliptic functions 110 204
Euler numbers, definition 132
Euler numbers, relation to Elkies series 222
Euler — McLaurin summation formula 93
Euler's constant, definition 173
Euler's constant, existence 173—174
Euler's constant, integral representations 176—179
Euler's constant, irrationality 184
Euler's constant, rale of convergence 181
Euler's constant, series representations 183
Euler, L., dilogarithm 239
Euler, L., infinite product for sine 126
Euler, L., integral definition of  186 186
Euler, L., lemniscatic identity 194
Euler, L., logarithmic integrals 241
Euler, L., original definition of  188 188
Euler, L., proof of 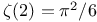 225 225
Eulerian polynomials in integrals of exponentials 99
Eulerian polynomials, definition 64
Eulerian polynomials, limits of an iteration method 134
Everest. G. et al., power series of rational functions 69
Ewell, J., formula for 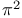 123 123
Ewell, J., formula for 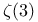 232 232
Exponent of p in r: 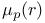 4 4
Exponential function, definition 91
Exponential integral see Advanced functions Exponential
Factorial definition 2
Feller, W., proof of Stirling's formula 96
Femiat, P., last theorem 101
Femiat, P., primes 121
Femiat, P., sums of squares 166
Fibonacci numbers, closed form 71
Fibonacci numbers, definition 1
Finch, S 85
Frullani integrals 98
Function, algebraic 79
Function, Beta 192
Function, cotangent 129
Function, dilogarithm 62
Function, error 162
Function, exponential 9
Function, floor 5
Function, Gamma 186
Function, generating 8
Function, hypergeometric 54
Function, incomplete gamma 9
Function, loggamma 201
Function, negapolygamma 215
Function, polygamma 214
Function, power 21
Function, psi 212
Function, rational 25
Function, tangent 63
Function, trigonometric 109
Function, zeta, Hurwitz 248
Function, zeta, Riemann 130 201 219
Fundamental Theorem of Arithmetic 3
Galois, E., unsolvability of the quintic 43
Gamma function see Advanced functions Gamma
Gauss. K.F, arithmetic-geometric mean 88
Gauss. K.F, multiplicative formula for  205 205
Gauss. K.F, radical values of sine 121
Gauss. K.F, rational values for  213 213
Gautschi, W., inequalities for  191 191
Generating function for 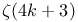 236 236
Generating function, binomial coefficients 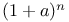 10 10
Generating function, definition 8
Generating function, factorials 9
Generating function, Fibonacci numbers 9
Generating function, generating polynomials 8
Geometric series 61
Goel, S., logarithmic integral 241
Goel, S., logsine integral 245
Goode, J., limit of harmonic sums 78
Gosper, W., evaluation of Nielsen — Ramanujan constants 240
Gosper, W., negapolygammas 215
Gouvea, F., p-adic analysis 4
Granville, A., generating function for 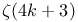 236 236
Greene, R. — Krantz. S., details on infinite products 129
Greenstein, D.S., growth of In x 79
Gregory. J., series for 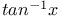 109 109
Grosswald, E., logarithmic integral 242
Hamming, R., In x is not algebraic 80
Hamming, R., In x is not rational 79
Hardy, G. and Wright, E.,  is transcendental 117 is transcendental 117
Hardy, G. and Wright, E., continued fractions 126
Hardy, G. and Wright, E., e is transcendental 89
Hardy, G. and Wright, E., p-adic analysis 4
Hardy, G. and Wright, E., prime numbers 3
Hardy, G. and Wright, E., proof of Bertrand's postulate 77
Hardy, G., integration of rational functions 44
Harmonic numbers are not integers 77
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



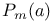 , coefficients
, coefficients  , definition
, definition 
 , definition
, definition 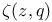
![$_2 F_1[a, b , c; x]$](/math_tex/44d87f1cfa27f4d991829f11bb7d99e082.gif) arctangent
arctangent  , definition
, definition 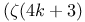
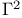
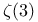
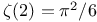

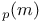
 function
function