|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Boros G., Moll V. — Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals |
|
|
 |
| Предметный указатель |
Harmonic numbers of higher order 202
Harmonic numbers, definition 76
Harmonic numbers, relation to  173 173
Harmonic numbers, relation to Riemann hypothesis 77
Harmonic series, definition 78
Harmonic series, divergence 78
Hauss, M., series of  123 123
Havil, J., information on  173 173
Havil, J., the Riemann hypothesis 220
Hellman, M., solution of cubics and quarries 39
Hermite, Ch., reduction procedure 147
Hermite, Ch., transcendence of e 89
Hijab, O., differentiation with respect to a parameter 21
Hijab, O., infinite products 129
Hijab, O., manipulation of power series 63
Hijab, O., powers of irrational exponent 22
Holder, O., theorem on  210 210
Homogeneous form 203 270
Hurwitz zeta function see Advanced functions Hurwitz
Huylebrouch, D., irrationality proofs 232
Hypergeometric function see Advanced functions Hypergeometric
Integral, combinations of exponentials and polynomials 103
Integral, combinations of logarithms and rational functions, linear denominators 239
Integral, combinations of logarithms and rational functions, quadratic denominators 239
Integral, combinations of polynomials and logarithms 81 238
Integral, combinations of trigonometric functions and polynomials 135
Integral, cosine 136
Integral, elliptic 88 110
Integral, exponential 98 104
Integral, Frullani 98 178
Integral, iterated of logarithms 82
Integral, Laplace 171
Integral, logarithmic 98
Integral, master formula 250
Integral, normal 162
Integral, polynomials 20
Integral, powers of loggamma 203
Integral, powers of logsine 245
Integral, products of logarithms 244
Integral, rational functions 25
Integral, rational functions, biquadratic denominator 44
Integral, rational functions, cubic denominator 42
Integral, rational functions, linear denominator 48
Integral, rational functions, normalization 27
Integral, rational functions, quadratic denominator 241
Integral, rational functions, quartic denominator 137
Integral, rational functions, Wallis* integral see Wallis' formula
Integral, representations for psi-function 215
Integral, representations for Riemann zeta function 222
Integral, representations of beta and gamma 193
Integral, sine 136
Jacobi, C., polynomials 155
Jacobi, C., sums of two squares 166
Jacobi, C., theta function 205
Johnson, W., zeta series 214
Johnsonbaugh, R.F., existence of  175 175
Kalman, D., methods to sum 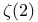 225 225
Kazarinoff, N.D., definitions of e 86
Kerney, K., logarithmic integral 244
Klamkin, M.S., some harmonic series 78
Knulh, D., compulation of Euler's constant 184
Koecher, M., expression for 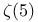 235 235
Koepf.W. 14
Kontsevich, M., conjecture on periods 262
Korlram, R., normal integral and sums of two squares 166
Kummer, E., regular primes 101
Lagarias, J., harmonic numbers and the Riemann hypothesis 77
Lagrange's inversion formula 150
Lambert, J.H., e is irrational 89
Landen, J., special values of dilogarithm 245
Laplace, P., integral 171 251
Laplace, P., transform 192
Larson, R. et al 112
Laugwitz, D 187
Lech — Mahler — Skolem theorem 69
Legendre, A.M., definition of  186 186
Legendre, A.M., duplication formula for  195 197 198 205 255 195 197 198 205 255
Legendre, A.M., formula for the exponent of p in m! 6
Lehmer, D., interesting Taylor expansions 118
Leibnitz, G. 109
Lewin, L., logarithmic integral 63
Lindemann, F.,  is transcendental 117 is transcendental 117
Linis, V., logarithmic integral 242
Liouville, J., e is not a quadratic irrational 90
Liouville, J., proof of Legendre's duplication formula for  197 197
Liouville, J., theorem on elementary primitives 162
Little, J., polynomials with roots on a vertical line 210
Logarithm, definition 19 73
Logarithm, growth and harmonic series 77
Logarithm, hypergeomelric representation 75
Logarithm, In x is not algebraic 80
Logarithm, In x is not rational 79
Logarithm, iterated integrals 82
Logarithm, power series 75
Logarithmic derivative of  212 212
Logarithmic derivative, second 129 132 204
Logarithmic integral see Advanced functions. Logarithmic integral
Logconcavity 157
Loggamma function see Advanced functions Loggamma
Lossers O.P. 229
Loxton, J.H., special values of dilogarithm 245
Lucas, E., denominators of Bernoulli numbers 101
Maor, E., information about e 85
Marchisolto, E.A., integration in finite terms 162
Marsaglia, G. and J.C., proof of Stirling's formula 95
Master formula 250
Mathemalica commands, Apart 26
Mathemalica commands, Assumptions 116
Mathemalica commands, BernoulliB 100
Mathemalica commands, Binomial 17
Mathemalica commands, CoefficientList 9
Mathemalica commands, Complexity function 27
Mathemalica commands, Element 21
Mathemalica commands, Extension 149
Mathemalica commands, Factor 15
Mathemalica commands, Factorial 3
Mathemalica commands, Factorlnteger 4
Mathemalica commands, Floor 5
Mathemalica commands, FullSimplify 21
Mathemalica commands, If 11
Mathemalica commands, Pochhammer 17
Mathemalica commands, PolynomialQuotient 138
Mathemalica commands, PolynomialRemainder 138
Mathemalica commands, Root 40
Mathemalica commands, Series 9
Mathemalica commands, SlirlingSl 18
Mathemalica commands, Solve 40
Mathemalica commands, Sum 15
Mathemalica commands, Table 11
Matsuoka, Y., proof of 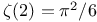 227 227
McMillan, E.M., calculation of  184 184
Medina, H., polynomial approximation of 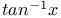 124 124
Mellin transform 55 196
Mendelson, N.S., limit form fort 88
Mordell, L., sign of Bernoulli numbers 100
Murty, R., update on Artin's conjecture 134
Myerson, G., Taylor expansions of rational functions 69
Nahim, P. 127
Napier, J., inequality 74
Nemes, I. el ah, examples of WZ-method 275
Newman, D., invariance of elliptic integrals 89
Newman, D., logconcavity and reciprocal of series 158
Newman, D., prime number theorem 220
Nielsen — Ramanujan constants 240
Niven, I., proof of irrationality of  117 117
Number, algebraic see Algebraic number
Number, bernoulli see Bernoulli number
Number, Eulerian see Eulerian number
Osier, T., relation between Vieta's and Wallis' formula for  116 116
p-adic valuations 4
| Parameters in integrals 20
Parameters, differentiation with respect to 21
Partial fractions 25
Pathak, P., proof of Stirling's formula 92
Pennisi, L., e is irrational 89
periods 262
Petkovsek, M., rational certificates 275
Plouffe, S., expression for  122 122
Pochhammer symbol see Ascending factorial symbol
Poly logarithms see Advanced functions Polylogarithms
Polya, G. and Szego, G. 86
Polygamma function see Advanced functions Polygamma
Polynomials 20
Polynomials, 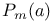 139 139
Polynomials, Bernoulli 101
Polynomials, Chebyshev of the first kind 110
Polynomials, coefficients 20
Polynomials, division algorithm 68
Polynomials, Eulerian 64 134 269
Polynomials, Jacobi 155
Polynomials, primitive 20
Polynomials, roots of 36
Polynomials, symmetric 29
Poorlen, van der. A., Taylor expansions of rational functions 69
Posey, R., evaluation of master formula 251
Power series,  66 66
Power series,  62 62
Power series, 1/(1-x) 61
Power series, arctangent 109
Power series, cotangent 130
Power series, definition 61
Power series, dilogarithm 62
Power series, double square root 150
Power series, exponential 91
Power series, involving Bernoulli numbers 99
Power series, involving central binomial coefficients 66 118
Power series, logarithm 75
Power series, loggamma 201
Power series, logsine 131
Power series, poly logarithm 239
Power series, powers of arcsine 122
Power series, powers of logarithms 76
Power series, psi function 213
Power series, rational functions 70
Power series, Riemann zeta function 224
Power series, secant and cosecant 132
Power series, sine and cosine 110
Power series, tangent 63
Power series, triple square root 160
Prime numbers, definition 3
Prime numbers, Fermat 121
Prime numbers, prime number theorem 220
Prime numbers, regular 101
primitive 19
Primitive root 134
Psi function see Advanced functions Psi
Qi,F, best bound on harmonic sequence 181
Ramanujan, S., expression for Euler's constant 179
Ramanujan, S., master theorem 151
Rao, S.K., integral representation of  177 177
Rao, S.K., Legendre's duplication formula 196
Rational certificate 275
Rational functions, a map on the space of rational functions 133
Rational functions, normalization 28—30
Rational functions, partial fraction decomposition 37
Rational functions, pole 49
Rational functions, Taylor series 67—72
Recurrences 1
Reversing order of summation 22
Ribenboim, P. 3 101
Riemann, B., hypothesis 77 219
Riemann, B., zeta function 130 201 219
Rivoal, T., irrationality of 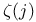 232 232
Rodewald, B 187
Rodriguez, D., logarithmic integral 241
Rodriguez, D., logsine integral 245
Rornik, D., proof of Stirling's formula 92 170
Roy, R., history of Gregory series 109
Ruffini, P., equations of degree at least five 43
Sandor, J., inequalities involving e 86
Scaling 51
Schlomilch transformation 251
Semifactorials 114
Serret, M.J.A., logarithmic integral 243
Serret, M.J.A., proof of Legendre's duplication formula 197
Shurman, J., solution of the quinlic 43
Sine integral see Advanced functions. Sine integral
Slieltjes constants 224
Sloane, N. 45 243
Sondow, J., antisymmetric formula for  234 234
Sondow, J., irrationality of Eulers constant 184
Spivak, M., definition of  106 106
Srivaslava, H. 203
Stanley, R., rational generating functions 72
Stanley, R., survey on unimodality 157
Stenger, A., logarithmic integral 244
Stirling formula, evaluation of constant 115 170
Stirling formula, proof by Blylh and Palhak 92
Stirling formula, proof by Feller 96
Stirling formula, proof by G. and J.C.Marsaglia 95
Stirling formula, proof by Romik 92 170
Stirling numbers of the first kind 18
Stirling's approximation 92—97
Stirling, J., biography 92
Stirling, J., formula 115
Stirling, J., numbers 18
Stromberg, K. 22
Swenney, D.W., computation of  184 184
Symbolic evaluation, blind 20
Taylor coefficients of rational functions 69
Taylor series see Power series
Titchmarsh, E.C. 55
Totik, proof of Holder's theorem on  211 211
Triangle number 243
Trigonometric functions, addition theorem 110
Trigonometric functions, cotangent 129
Trigonometric functions, infinite products 126
Trigonometric functions, inverse sine 107
Trigonometric functions, inverse tangent 107
Trigonometric functions, sine and cosine 109
Trigonometric functions, solution of cubics and quarlics 111
Trigonometric functions, Taylor expansions 110
Triple square root 160
Tweedle, I., biography of J.Stirling 92
Tyler, D., special zeta series 248
Umemura, H. 44
Underwood, R.S 84
Unimodality 156
Vacca, G., a series for  184 184
Valuations see p-adic valuations
Vandermonde formula for ascending factorial 18
Vardi, I. 237
Venkalachaliengar, K., infinite product for sin x 127
Vieta, F., radical expression for  116 116
von Mangoldt function, connection to Eulers constant 224
von Mangoldt function, connection to Riemann hypothesis 219
von Mangoldt function, iterate integrals of ln(1+ x) 84
Wallis' formula, Osier's relation between Vieta's and Wallis' formula for  116 116
Wallis' formula, proof by recurrence 32
Wallis' formula, proof by WZ-melhod 273
Wallis' formula, proof from Legendre's duplication formula 198
Wallis' formula, proof from master formula 255
Weierstarss, K., 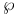 -function 205 -function 205
Weight 203 270
Weisstein, E. 18 84 111
Wilf, H. 15 157 271
Williams, K.S., formula for 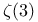 233 233
Williams, K.S., proof of 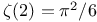 231 231
Wrench, J., partial sums of harmonic series 78
WZ-method 156 166 271
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте






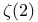
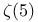
 is transcendental
is transcendental 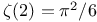
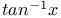
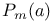


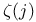

 -function
-function