|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Humphreys J.F., Prest M.Y. — Numbers, Groups and Codes |
|
|
 |
| Предметный указатель |
Abel 170 181 257
Abelian see group abelian
Abstract algebra, rise of 193ff
Accept(ed) 120
Addition modulo f 280
Addition modulo n 40
Adjacency matrix 108
Adleman 70
Al-jabr wa'k muqabalah 180
al-Khwarizmi 180
Alexander the Great 14
Algebra 192
Algebra of sets 8311
Algebraically closed 293
Alphabet (of finite stale machine) 119
Argand diagram 293
Argument (of complex number) 293
Arithmetic modulo n 40
Arithmetica 33 36
Ars Magna 181
Automaton 120
Axiom 184
Babbage 117ff
Bachet 36 45 74
Bernoulli, D. 101
Bernoulli, J. 101
Binomial coefficient 19
Binomial theorem 18 65 75
Boole 85 136 185 195
Boolean algebra 136 192ff 198ff
Boolean algebra of sets 84 135f 193 199
Boolean combination 130
Boolean ring 199
Brahmagupta 45 50 180
Bravais 183
Calculating machines 117ff
Cantor 85 97ff
Cardano 181
Cardinality 98
Carroll see Dodgson
Cartesian product see product
Casting out nines 49
Cauchy 148 158 164 182 216
Cayley 174 182 195
Characteristic 197
Check digit 231ff
Chinese remainder theorem 54
Code, error-correcting and error-detecting 230ff
Code, error-correcting and error-detecting, cyclic 2840'
Code, error-correcting and error-detecting, Golay 252
Code, error-correcting and error-detecting, group see code linear
Code, error-correcting and error-detecting, Hamming 249
Code, error-correcting and error-detecting, linear 237ff 284ff
Code, error-correcting and error-detecting, perfect 249
Code, error-correcting and error-detecting, quadratic residue 290 see
Codeword 232 245 284ff
Coding function 232ff
Codomain 87
Coefficient, of polynomial 256 261 287
Common measure 32
Complement 80 192
Complement, double 193
Complement, properties of 83 193
Complement, relative 80
Completeness theorem 140
Complex numbers, set of  172 174 176 189 192 193ff 221 258 261 276 292ff 172 174 176 189 192 193ff 221 258 261 276 292ff
Composite 28
Composition (of functions) 93ff 149ff
Congruence 38 45 161 205 213
Congruence class 36 38 50 115 196 279
Congruence class, invertible 43 44ff 52
Congruence class, order of 61ff
Congruence class, set of invertible  47 63ff 172 212 220 223 47 63ff 172 212 220 223
Congruence, linear 49ff
Congruence, non-linear 57ff
Congruence, simultaneous linear 54ff
Congruence, solving linear 50
Congruent (integers) 36
Congruent (polynomials) 279
Conjecture 34
conjugate 164 166 212 230
Conjugate, complex 293ff
Conjunction 129
Consistency 134
Contradiction 134
Contrapositive 132 142
CONVERSE 132
Coprime see prime relatively
Corollary 8
Coset (left, right) 212ff 228
Coset decoding table 241ff
Coset decoding table with syndromes 246
Coset leader 244
Counterexample 35
Cours d'Algebre superieure 182
Covering 113
Cut 159 169
CYCLE see permutation cyclic
Cycle decomposition (of permutation) 154 155 163
Cyclic group see group cyclic
Cyclic permutation see permutation cyclic
D'Alembert 101
De Morgan 115 136 194
De Morgan laws see law De
Decoding table see coset decoding table
Dedekind 189
Deduction, rules of 140
Degree (of polynomial) 256 262 264 279
del Ferro 181
Descartes 36 84
Difference Engine 117ff
Diffie 70
Digit sum, (iterated) 49
Digraph 107 see
Diophantus 33 36 74
Direct product 153 163 see
Dirichlet 101
Disjoint sets 81 98 113 214
Disjunction 129
Disquisitiones Arithmetical 36 40
Distance 234 236 237 249
Divide 3 36 46 218 262 265
Division algorithm see Euclidean algorithm
Division theorem 3 264
Dodgson 80
Domain 87
Dyck 182
Element 78
Elements (Euclid's) 9 14 15 22 26 29 32
Equivalence class 114
Equivalence Erlanger programme 183
Equivalence relation see relation equivalence
Equivalent (propositions) see logical
Eratosthenes 26
Error-correction 231ff 236 240ff
Error-detection 230ff 236
Euclid 9 14 15 22 23 29 32ff
Euclidean algorithm 9ff 269ff
Euler 33ff 40 65ff 74 80 101
Euler phi-function  66ff 98 172 66ff 98 172
Euler's theorem 68 72 143 144 218
Evaluate (polynomial) 257
Existential quantifier 138
Exponent (of public key code) 71
Factorial (n!) 18
Fallings 33 74
Ferarri 181
Fermat 23 33ff 36 63 65 73ff
Fermat's 'Theorem' 33 127
Fermat's theorem 63 76 143 144 217
| Fibonacci sequence 23
Field 189ff 194 282 283
Field of fractions 198
Finite state machine 119ff 186ff
fix 153
FOURIER 101
Fractions see rational numbers
Frenicle 34 63
Function 87ff 103 185ff
Function, characteristic 103
Function, concept of 86ff 100ff
Function, constant 92
Function, identity 92
Function, infective see injection
Function, one-to-one see injection
Function, onto see surjection
Function, surjective, it see surjection
Fundamental theorem of algebra 189 258 276 293
Fundamental Theorem of Arithmetic see Unique Factorisation Theorem
Galois 157 181ff 189 257
Galois field 282
Gauss 36 40 194
GCD see greatest common divisor
GENERATED 209ff 286
Generator matrix 237
Generator polynomial 286
Generators, of group 209
Gibbs 195
Godel 140
Goldbach 34 74
Goldbach's conjecture 34ff
Graph, of function 89
Graph, of function, directed see directed graph
Grassmann 195
Greatest common divisor 7 31 32 43 50 268ff
Gregory 194
Greiss 229
Group 170ff 184 185 200ff 257
Group of matrices 175ff
Group of numbers 171f
Group of permutation see group symmetric
Group of small order 224ff
Group of symmetries 177ff
Group, Abelian (=commutative) 170 173 182 209 224 225 259
Group, alternating 167 174 208 216 218 228
Group, concept of xi 147 180ff 200
Group, cyclic 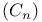 209 216 217 220ff 224 209 216 217 220ff 224
Group, dihedral  178 179 211 221 228 178 179 211 221 228
Group, general linear 175 210 211
Group, Klein four 224
Group, Mathieu 228
Group, monster 229
Group, p- 218
Group, simple 228ff
Group, special linear 208
Group, sporadic simple 228ff
Group, symmetric 149 174 209 211 213 216 220ff 223
Hamilton 172 194ff
Hasse 111
Hasse diagram 111
HCF see highest common factor
Hellman 70
Hensel 189
Highest common factor see greatest common divisor
Hollerith 118
Idempotent 185
Identity element 170
Identity, logical see logical identity
Image 87
Imaginary part 292
Immediate predecessor 111
Immediate successor 111
Implication 132
Induction, course of values see induction strong
Induction, definition by 18
Induction, hypothesis 16
Induction, principle 16 20 23 24
Induction, proof by 16ff 22ff 143
Induction, step 16 21
Induction, strong 21
Inductive construction 15
Infinite order 90 186 see infinite
Integers modulo n, set of  38 171 189 210 213 220 261 272 278 281ff 283ff 38 171 189 210 213 220 261 272 278 281ff 283ff
Integers, set of  1 171 185 188 210 213 1 171 185 188 210 213
Integral domain 192
Integral linear combination 7 44
Intersection 80 209
Inverse 43ff 170 282
inverse of function 95 96 220
Inverse of polynomial congruence class 282
Invertible congruence class 43 44ff 52
Invertible matrix 175
Irrational numbers 32 101 190
Irreducible (polynomial) 273ff 282
ISBN code 231
Isomorphism 219ff
Janko 229
Jiu zhang suan shu see Nine Chapters on the Mathematical Art
Join 192
JORDAN 182 216
Kilburn 118
Klein 183
Knapsack codes 70
kronecker 182
Lagrange 158 182 216
Lagrange's theorem 66 143 144 216 218 225 226 231
Law, absorption 83 134
Law, associative 83 94 134 170 188 193
Law, commutative 83 134 170 188
Law, contrapositive 134
Law, De Morgan 83 134 193
Law, distributive 83 134 193
Law, double negative 134
Law, excluded middle 134
Law, idempotence 83 134 193
Law, index 159 204
Law, Laws of Thought 185
LCM see least common multiple
Leading coefficient 256
Leading term 256
Least common multiple 14 31
Leibniz 65 80 101 117 136
Lemma 8
Length of code 284
Length of permutation 152
Length of word 232
Linear Associative Algebras 185
Liouville 182
Logical equivalence 133 136 193
Logical identity 133
Map (mapping) see function
Master Sun s Arithmetical Manual 1
Mathematical Treatise in Nine Sections 54 56
Mathieu 228
Matrix, diagonal 176 208
Matrix, groups and rings of 175ff 188 192 195 206 208
Matrix, invertible 175
Matrix, method (for gcd) 10ff
Matrix, upper triangular 1750
Maximum likelihood decoding 241
Meet 192
Member 101. see element Methodus Incrementorum
mersenne 34
Mod(ulo) see congruent
Modulus (of complex number) 293
Move 153
Multinomial theorem 75
Multiplication modulo f 280
Multiplication modulo n 40
Natural numbers, set of (N) 2
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте