|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gierz G., Hofmann K.H., Keimel K. — Continuous Lattices and Domains |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Pro-continuous functor 318 IV—5.1
Pro-continuous functor, between pro-complete categories 331 IV—6.1
Probabilistic powerdomain, is a domain 386 IV—9.17
Product, in a category 306 remarks following IV—4.1
Product, in a category of domains 79 I—2.1
Projection 11 remarks preceding O—2.5 26
Projection maps, on a product 306 Remarks following IV—4.1
Projection operator 11 remarks preceding O—2.5
Projection operator on a continuous lattice 89 I—2.17
Projection, on a continuous poset preserving directed sups 80 I—2.2
Projection, preserving (directed) sups 28 O—3.11
Projection, preserving (filtered) infs 28 O—3.11
Projective limit cone, in a category 307 IV—4.2
Projective limit preserving functor 318 IV—5.1 318
Projective limit, in a category 307 IV—4.2
Projective limit, in a category of algebraic domains 316 IV—4.11
Projective limit, in a category of bounded complete domains 317 IV—4.13
Projective limit, in a category of dcpos 308 IV—4.3
Projective limit, in a category of domains 316 IV—4.10
Projective limit, in a category of finite domains 316 IV—4.12
Projective limit, in a category of finite lattices 317 IV—4.14
Projective limit, in a category of L-domains 317 IV—4.13
Projective limit, in a category of Lawson compact domains 317 IV—4.15
Projective sequences 328 IV—5.16
Projective system, in a category 307 IV—4.2
Proper map 422 remarks preceding V—5.20 481
Property M 257 III—5.11
Pseudo-Hausdorff space 485 VI—6.31
Pseudoprime element 106 I—3.24 403
Pseudoprime element in a continuous semilattice 106 remarks following I—3.24
Pseudoprime element in a distributive continuous lattice 106 I—3.25
Quasialgebraic domain 237 III—3.23
Quasicontinuous domain 226 III—3.2
Quasicontinuous domain is a pospace 444 VI—1.15
Quasicontinuous domain is Lawson-compact 255 III—5.8
Quasicontinuous domain, closed under quotients 262 III—5.21
Quasicontinuous domain, closure properties of 239 III—3.30
Quasicontinuous domain, Scott topology is hypercontinuous 513 VII—3.9
Quasicontinuous lattice 230 III—3.8
Quasicontinuous lattice, Scott cluster points of ultrafilters 238 III—3.29
Quasicontinuous lattice, sup map characterization 263 III—5.23
Quasihomeomorphism 418 V—5.8
Quotient, of a continuous lattice 88 I—2.15
Random unit interval 92 remarks following I—2.22
Regular open sets, in a topological space 13 O—2.7(3)
Relation, auxiliary see “Auxiliary relation”
Relation, converse 4 O—1.7
Relation, opposite 4 O—1.7
Relation, with closed graph 440 VI—1.1
Relatively compact element 50 remarks following I—1.2
retract 179 remarks preceding II—3.5
Retraction 179 remarks preceding II—3.5
Ring of sets 375 remarks following IV—9.1
Rounded ideal 242 III—4.3(ii) 249
Rounded ideal completion 250 III—4.17
Rudin’s Lemma 227 III—3.3
S-convergence 133 II—1.1
S-convergence and topological convergence 138 II—1.9
Saturated compact sets 66 I—1.24
Saturated compact sets in the spectrum 416 V—5.3
Saturated compact sets in the spectrum and Scott-open filters 417 V—5.4
Saturated subset, of a space 43 O—5.3 416
Scott closed set 134 II—1.3
Scott closed set, characterization of 135 II—1.4
Scott open set 134 II—1.3
Scott open set, characterization of 135 II—1.4
Scott open set, in a chain 136 II—1.5(2)
Scott open set, in a domain 136 II—1.6
Scott open set, in a finite lattice 136 II—1.5(1)
Scott open set, in a quasicontinuous domain 228 III—3.6
Scott open set, in the square 136 II—1.5(5)
Scott topology 132 II—1 134
Scott topology has a basis of open filters 223 III—2.13
Scott topology has enough co-primes 142 II—1.14
Scott topology is a continuous lattice 142 II—1.14 199
Scott topology is a function space 165 II—2.11
Scott topology is an algebraic lattice 143 II—1.15
Scott topology is Baire 142 II—1.13
Scott topology is completely distributive 142 II—1.14
Scott topology is finest order consistent topology 152 II—1.31(i)
Scott topology is locally compact and sober for quasicontinuous domains 229 III—3.7
Scott topology is locally compact and sober for quasicontinuous domains, (on a domain) 142 II—1.13
Scott topology is productive 197 II—4.13
Scott topology is sober 141 II—1.12 198
Scott topology, basis for (on domains) 138 II—1.10
Scott topology, co-primes in 140 II—1.11
Scott topology, forms a continuous lattice 197 II—4.13 198
Scott topology, functor, preserves injective (surjective) maps 325 IV—5.11
Scott topology, functor, preserves injective (surjective) maps, preserves projective limits 325 IV—5.11
Scott topology, induced on subsets 151 II—1.26
Scott topology, on a meet continuous lattice 198 II—4.17 199
Scott topology, on a meet continuous semilattice 206 II—4.28
Scott topology, primes in 140 II—1.11
Scott topology, when a topological lattice 199 II—4.18
Scott topology, when hypercontinuous 513 VII—3.9
Scott topology, when join continuous 198 II—4.17 199
Scott topology, when strongly sober 497 VII—1.10
Scott-continuous function 157 II—2 158
Scott-continuous function is always monotone 157 II—2.1
Scott-continuous function, between algebraic domains 157 II—2.1
Scott-continuous function, between dcpos 157 II—2.1
Scott-continuous function, characterization of 157 II—2.1
Scott-continuous function, form a dcpo 161 II—2.5
Scott-continuous function, joint continuity on products 162 II—2.8 171
Scott-continuous functionv, between domains 157 II—2.1
Second countable space 44 O—5.8
Semicontinuous function 17 O—2.10 64
Semilattice 5 O—1.8
Semilattice has small semilattices 223 III—2.12 (see also “Semilattice with small semilattice”)
Semilattice is a pospace if topological 444 VI—1.14
Semilattice is topological in the lower topology 211 III—1.4
Semilattice with small semilattices 450 VI—3.1
Semilattice with small semilattices, characterization of 451 VI—3.3
Semilattice with small semilattices, closure properties of 450 VI—3.2
Semilattice, algebraic see “Algebraic semilattice”
Semilattice, compact see “Compact semilattice”
Semilattice, complete see “Complete semilattice”
Semilattice, complete continuous see “Complete continuous semilattice”
Semilattice, continuous see “Continuous semilattice”
Semilattice, deflationary 363 IV—8.8
Semilattice, directed complete 9 O—2.1 (see also “Directed complete semilattice”)
Semilattice, homomorphism is Lawson continuous 213 III—1.8
Semilattice, inflationary 361 IV—8.3
Semilattice, meet continuous see “Meet continuous semilattice”
Semilattice, order connected 471 VI—5.13
Semilattice, prime element in 99 I—3.12
Semilattice, prime filter in 103 I—3.18
Semilattice, prime ideal in 103 I—3.18
Semilattice, semitopological see “Semitopological semilattice”
Semilattice, topological 443 VI—1.11
Semilattice, when a compact pospace 517 VII—4.2
Semilattice, when a compact semilattice 518 VII—4.4
Semitopological semilattice 33 O—3.23 38 153 443
Semitopological semilattice has the Scott topology 498 VII—1.12
Semitopological semilattice is a strongly sober topological lattice 498 VII—1.12
Semitopological semilattice is semiclosed 443 VI—1.13
Semitopological semilattice, compact see “Compact semitopological semilattice”
Semitopological semilattice, local minimum in 470 VI—5.10
Semitopological semilattice, when topology is Scott topology 496 VII—1.9(iii)
Separable space 44 O—5.8
Separated sum 73 I—1.31 321
Set, directed 1 O—1.1
Set, directed, filtered 1 O—1.1
Set, directed, lower 3 O—1.3
Set, directed, partially ordered see “Poset”
Set, directed, preordered 1 O—1.1
Set, directed, totally ordered see “Chain”
Set, directed, upper 3 O—1.3
| Sierpinski space 136 II—1.5(3)
Sierpinski space is injective 178 II—3.3
Simple valuation 380 IV—9.9
Smash product 327 IV—5.15
Smyth powerdomain 363 IV—8.8 363
Smyth powerdomain of an algebraic domain 373 IV—8.23
Sober space 43 O—5.6 101 141
Sober space is locally compact iff 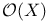 is continuous 417 V—5.6 is continuous 417 V—5.6
Sober space with completely distributive topology 425 V—5.26
Sober space, closure properties 46 O—5.16
Sober space, compact saturated sets and open filters in 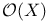 146 II—1.20 146 II—1.20
Sober space, dual to frames 426 V—5.27
Sober space, function space on 424 V—5.23(i)
Sober space, spectrum of a complete lattice 409 V—4.4
Sober space, when a domain 425 V—5.26
Sobrification, of a 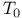 -space 412 Remarks following V—4.7 414 429 -space 412 Remarks following V—4.7 414 429
Specialization order 42 O—5.2 180
Spectrum 408 V—4.1
Spectrum is a 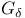 -set and a Polish space 420 V—5.14 -set and a Polish space 420 V—5.14
Spectrum of a complete lattice 408 V—4.1
Spectrum of a distributive continuous lattice 417 V—5.5
Spectrum of distributive algebraic lattices 423 V—5.21
Spectrum, compact subsets 416 V—5.1
Spectrum, is sober 409 V—4.4
Spectrum, of stably continuous frames 487 VI—7.1
Splitting lemma 386 IV—9.18
Stably compact space 476 VI—6.7 479
Stably compact space is a compact pospace 476 VI—6.8
Stably compact space is strongly sober 478 VI—6.15
Stably continuous (semi)lattice 256 III—5.9
Stably continuous frame, spectrum is stably locally compact 487 VI—7.1
Stably locally compact space 476 VI—6.7
Stably locally compact space, stable compactification 490 VI—7.7
Stochastic order 380 IV—9.7
Stochastic order for simple valuations 386 IV—9.18
Stone — Cech compactification, of a set 455 remarks following VI—3.9 460
Strict (endo)morphism 346 IV—7.2
Strict chain, in a complete lattice 293 IV—3.4
Strict chain, in a complete lattice, satisfies the interpolation property 294 remarks following IV—3.8
Strict chain, in a complete lattice, separates points in complete lattices 298 IV—3.15
Strict embedding, of a topological space 418 V—5.8 428 428
Strict function 327 IV—5.15
Strict function space 327 IV—5.15
Strong interpolation property see “Auxiliary relation”
Strong topology 428 V—5.31
Strongly dense 428 V—5.33
Strongly sober 498 VII—1.11
Strongly sober, locally compact space is stably compact 478 VI—6.15
Strongly sober, space 477 VI—6.12 479
Subalgebra, of a continuous lattice or bounded complete domain 86 I—2.10
Subcontinua of a continuum 70 I—1.26
Subinvariant pseudometric 446 VI—2.1
Sup map, has a lower adjoint 57 I—1.10
Sup map, has a lower adjoint is a homomorphism 36 O—4.2
Sup map, has a lower adjoint is jointly continuous 198 II—4.15 204
Sup map, has a lower adjoint, on the ideals of a complete lattice 30 O—3.15
Sup map, has a lower adjoint, preserves arbitrary infs 57 I—1.10
Sup semilattice 5 O—1.8
Sup semilattice, conditional 117 I—4.5
Support of a simple valuation 380 IV—9.9
Supremum 1 O—1.1
Tarski’s fixed-point theorem 10 O—2.3
Tensor product of complete lattices 279 IV—1.27 279
Tensor product of complete lattices of continuous lattices 279 IV—1.27 279
Tensor product of complete lattices, of distributive continuous lattices 424 V—5.24
Tensor product of complete lattices, of topologies of locally compact spaces 424 V—5.24
Top, of a poset 5 O—1.8
Topological lattice 443 VI—1.11
Topological semilattice 221 III—2.7 443
Topological space, compact 43 O—5.7
Topological space, compact with 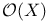 a continuous lattice 190 II—4.4 192 193 194 196 a continuous lattice 190 II—4.4 192 193 194 196
Topological space, compact, locally compact 44 O—5.9
Topological space, compact, patch topology on 419 V—5.11
Topological space, compact, saturated subset 43 O—5.3
Topological space, compact, saturation of a subset 43 O—5.3 45
Topological space, compact, sober 43 O—5.6
Topological space, compact, weight of 243 remarks preceding III—4.5
Topologically generating subset, of a topological semilattice 400 V—2.2
Totallly ordered set see “Chain”
Totally disconnected space 127 I—4.28(iv)
Totally order disconnected compact pospace 490 VI—7.8
Ultrafilter 45 O—5.12
Ultrafilter, cluster points, in the lower topology 235 III—3.15
Ultrafilter, cluster points, in the lower topology, in the liminf topology 232 III—3.18
Ultrafilter, in the power set of a set 104 remarks following I—3.19
Ultrafilter, in the power set of a topological space 104 I—3.21
Ultrametric, on a semilattice 458 VI—3.15
Unit interval 453 VI—3.6
Unit interval, approximate 433 V—6.2
Unit, in a semilattice 5 O—1.8
Unital semilattice 5 O—1.8
Upper adjoint 22 O—3.1
Upper adjoint is injective 26 O—3.7
Upper adjoint is surjective 26 O—3.7
Upper adjoint, preserves infs 24 O—3.3
Upper adjoint, preserving directed sups 268 IV—1.4 272
Upper adjoint, preserving primes 268 IV—1.4 277
Upper bound 1 O—1.1
Upper semicontinuous function 17 O—2.10
Upper set 3 O—1.3
Upper space 433 V—6.3
Upper topology 43 O—5.4 152
Upper topology is coarsest order consistent topology 152 II—1.31(i)
Urysohn — Carruth Metrization Theorem 445 VI—1.18
Urysohn — Nachbin Lemma 444 VI—1.16
Valuation 375 IV—9.1
Valuation, continuous 379 IV—9.5
Valuation, extension to a finitely additive measure 376 IV—9.3 377
Valuation, finite 375 IV—9.1
Valuation, powerdomain 380 IV—9.7
Valuation, powerdomain is a domain 385 IV—9.16
Valuation, simple 380 IV—9.9
Vertex, of a cone 305 IV—4.1
Vietoris topology 454 VI—3.8
Way-below relation 49 I—1 49
Way-below relation, axiom of approximation 54 I—1.6
Way-below relation, for closed lower sets of a compact semilattice 459 VI—3.22
Way-below relation, for simple valuations 388 IV—9.19
Way-below relation, for subsets 226 III—3.1
Way-below relation, fundamental properties of 50 I—1.2
Way-below relation, in a Boolean algebra 52 I—1.3(3)
Way-below relation, in a chain 51 I—1.3(1)
Way-below relation, in a complete distributive lattice 105 I—3.23
Way-below relation, in a direct product 51 I—1.3(2)
Way-below relation, in a domain 62 I—1.20
Way-below relation, in a finite poset 52 I—1.3(4)
Way-below relation, in a meet continuous lattice 53 I—1.5I—1.5(i)(3)
Way-below relation, in the domain of open filters 145 II—1.17
Way-below relation, in the lattice of open sets of a space 53 I—1.4 104 105
Way-below relation, in the lattice of two-sided ideals of a ring 52 I—1.3(5)
Way-below relation, interpolation property 56 I—1.9 62 228
Way-below relation, multiplicative 107 I—3.27 256 289
Way-below relation, on function spaces 200 II—4.20 205
Way-below relation, on the closed sets of a locally compact space 216 III—1.15(i)
Way-below relation, on the extended probabilistic power-domain 385 IV—9.16
Way-below relation, topological analogue 153 II—1.32 153
Way-below set, of an element 51 remarks following I—1.2
Way-below set, of an element is an ideal 51 remarks following I—1.2
Way-way-below relation 303 IV—3.31
Way-way-below relation, on a completely distributive lattice 303 IV—3.31
Weak irreducible 403 V—3.1
Weak prime 110 remarks following I—3.37 403 404
Weak prime, order-generate 111 I—3.38
Weight, of a domain 242 III—4.4
Weight, of a domain, of a topological space 243 remarks preceding III—4.5
Weight, of a domain, of function spaces 245 III—4.9
Well-filtered space 67 I—1.24.1
Well-filtered space and soberness 147 II—1.21
Zero, of a poset 5 O—1.8
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



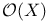 is continuous
is continuous 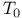 -space
-space 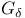 -set and a Polish space
-set and a Polish space