|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gierz G., Hofmann K.H., Keimel K. — Continuous Lattices and Domains |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Join-irreducible element 97 remarks following I—3.5
Joint continuity, of the sup operation 139 remarks following II—1.10
Kernel operator 26 O—3.8
Kernel operator has continuous image 270 IV—1.7
Kernel operator, lattice of continuous is algebraic 302 IV—3.26
Kernel operator, lattice of continuous is continuous 302 IV—3.26
Kernel operator, lattice of, on a complete lattice 301 IV—3.25
Kernel operator, lattice of, on a complete lattice, on a continuous lattice 302 IV—3.26
Kernel operator, lattice of, on a complete lattice, on an algebraic lattice 302 IV—3.26
Kernel operator, on a continuous lattice 88 I—2.15 89
Kernel operator, preserves infs 29 O—3.12
Kernel operator, preserving directed sups 270 IV—1.7
Koch’s Arc Theorem 470 VI—5.9
L-domain 5 O—1.8 54
L-domain of a topological ring 15 O—2.7(7)
L-domain of closed congruences, of a topological algebra 15 O—2.7(6)
L-domain of closed ideals, of a C*-algebra 63 remarks I—1.21.1 preceding 1
L-domain of closed subsets of a space 13 O—2.7(3)
L-domain of closed subspaces, of a Hilbert space 15 O—2.7(8)
L-domain of compact normal subgroups is algebraic for almost connected groups 128 I—4.29
L-domain of congruence relations, on an algebra 14 O—2.7(4)
L-domain of congruences on a continuous lattice 303 IV—3.29(i)
L-domain of filters, of a semilattice 16 O—2.8(2)
L-domain of ideals, of a lattice 14 O—2.7(4)(iii) 16
L-domain of lower sets, of a poset 16 O—2.8(1)
L-domain of monotone functions, on the unit interval 15 O—2.7(9)
L-domain of normal subgroups, of a group 14 O—2.7(4)(i)
L-domain of open sets 13 O—2.7(3)
L-domain of open sets is a continuous lattice 73 I—1.34
L-domain of open sets is algebraic 127 I—4.28(ii)
L-domain of open sets is arithmetic 127 I—4.28(iii)
L-domain of open sets, way-below relation in 53 I—1.4
L-domain of partial functions, from X to Y 73 I—1.32
L-domain of partial functions, from X to Y, on the natural numbers 15 O—2.7(10)
L-domain of regular open sets 33 O—3.22(iii)
L-domain of Scott open sets, co-primes in 140 II—1.11
L-domain of Scott open sets, co-primes in is a continuous lattice 142 II—1.14
L-domain of Scott open sets, co-primes in is completely distributive 142 II—1.14
L-domain of Scott open sets, co-primes in, on a domain 140 II—1.11
L-domain of Scott open sets, co-primes in, primes in 140 II—1.11
L-domain of subalgebras, of an algebra 14 O—2.7(5)
L-domain of subcontinua 71 I—1.26.3
L-domain of subsets 375 remarks preceding IV—9.1
L-domain of two-sided ideals, of a ring 14 O—2.7(4)(ii)
L-domain of two-sided ideals, of a ring is a continuous lattice 55 I—1.7
L-domain of two-sided ideals, of a ring, way-below relation in 52 I—1.3(5)
L-domain of upper sets, of a poset 16 O—2.8(1)
L-domain with five elements 74 I—1.36
L-domain, algebraic see “Algebraic lattice”
L-domain, arithmetic see “Arithmetic lattice”
L-domain, bicontinuous see “Bicontinuous lattice”
L-domain, Boolean see “Boolean algebra”
L-domain, characterizations of 75 I—1.38
L-domain, closure properties of 92 I—2.24
L-domain, compact see “Compact lattice”
L-domain, complemented 12 O—2.6
L-domain, complete 9 O—2.1 (see also “Complete lattice”)
L-domain, completely distributive see “Completely distributive lattice”
L-domain, continuous see “Continuous lattice”
L-domain, distributive 12 O—2.6 (see also “Distributive lattice”)
L-domain, distributive algerabic see “Distributive algebraic lattice”
L-domain, distributive arithmetic see “Distributive arithmetic lattice”
L-domain, distributive continuous see “Distributive continuous lattice”
L-domain, hypercontinuous see “Hypercontinuous lattice”
L-domain, join continuous see “Join continuous lattice”
L-domain, M-distributive 93 I—2.25
L-domain, meet continuous see “Meet continuous lattice”
L-domain, modular see “Modular lattice”
L-domain, Scott topology on see “Scott topology”
L-domain, topological 443 VI—1.11
Lawson dual 283 remarks following IV—2.7
Lawson duality 398 V—1.9
Lawson duality for continuous semilattices 287 IV—2.16
Lawson duality for domains 286 IV—2.14
Lawson topology 209 III—1 211
Lawson topology and patch topology 420 V—5.15
Lawson topology has small compact semilattices 224 III—2.15
Lawson topology has small open closed semilattices 224 III—2.16
Lawson topology has small open semilattices 223 III—2.13 224
Lawson topology is compact and 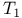 for complete (semi)lattices 214 III—1.9 for complete (semi)lattices 214 III—1.9
Lawson topology is compact Hausdorff for complete continuous (semi)lattices 215 III—1.11
Lawson topology is compact zero-dimensional 224 III—2.16
Lawson topology is completely metrizable for countably based domains 421 V—5.17
Lawson topology is Hausdorff, for domains 215 III—1.10
Lawson topology is Hausdorff, for domains, for quasicontinuous domains 229 III—3.7
Lawson topology is separable metric 244 III—4.6
Lawson topology is the interval topology 510 VII—3.4
Lawson topology on an algebraic domain 216 III—1.14
Lawson topology, closed lower sets 212 III—1.6
Lawson topology, continuous function for 213 III—1.8
Lawson topology, open lower sets 238 III—3.28(iv)
Lawson topology, open upper sets 212 III—1.6
Lawson topology, when compact 254 III—5.5 255 258
Lawson topology, when Hausdorff 230 III—3.11
Lawson topology, when productive 221 III—2.6
Lean lattice 515 VII—3.13
Least F-algebra Morphism Lemma 348 IV—7.4
Least fixed point operator, is Scott-continuous 172 II—2.29
Least Fixed Point Theorem, for monotone self-maps 20 O—2.20
Least Fixed Point Theorem, for monotone self-maps, for Scott-continuous self-maps 160 II—2.4
Least upper bound 1 O—1.1
Lens in a domain 368 IV—8.15
Lifting functor 321 IV—5.6
Liminf convergence 232 III—3.13
Liminf convergence is topological 234 III—3.17
Liminf topology 226 III—3 232
Liminf topology, agrees with the Lawson topology 234 III—3.17
Liminf topology, closed lower sets 232 III—3.14
Liminf topology, closed sets 232 III—3.15
Liminf topology, open upper sets 232 III—3.14
Liminf topology, when compact 233 III—3.16
Liminf, of a net 133 II—1.1
Limit cone, over a diagram 305 IV—4.1
Limit maps 306 IV—4.1
Limit preserving functor 318 IV—5.1
Limit, of a diagram 306 IV—4.1
Limit-colimit coincidence 309 IV—4.5 313
Linked bicontinuous lattice 501 VII—2.5
Linked bicontinuous lattice is a compact lattice in Lawson topology 502 VII—2.8
Linked bicontinuous lattice is completely distributive, if distributive 503 VII—2.10
Linked bicontinuous lattice is embeddable in a cube 503 VII—2.10
Linked bicontinuous lattice, Lawson topology has small lattices 502 VII—2.8
Local minimum in a pospace 469 VI—5.8
Locally compact sober space, duality with distributive continuous lattices 423 V—5.20 426
Locally compact space 44 O—5.9 53
Locally compact space, co-compact topology 427 V—5.29
Locally compact space, lower topology on the lattice of closed sets 216 III—1.15(iii)
Locally compact space, open sets form a continuous lattice 55 I—1.7
Locally compact space, Scott topology on the lattice of closed sets 216 III—1.15(ii)
Locally continuous functor 320 IV—5.3
Locally continuous functor, contravariant case 323 IV—5.7
Locally continuous functor, preserves adjoints and projective limits 320 IV—5.5
Locally order preserving functor 320 IV—5.3
Locally order preserving functor, contravariant case 323 IV—5.7
Locally order preserving functor, preserves adjoints 320 IV—5.4
Locally strongly sober space 477 VI—6.12
Locally strongly sober space is coherent 478 VI—6.14
Lower adjoint 22 O—3.1
Lower adjoint is a lattice homomorphism 277 IV—1.22
Lower adjoint is injective 26 O—3.7
Lower adjoint is Scott-continuous 159 II—2.3(1)
Lower adjoint is surjective 26 O—3.7
Lower adjoint, preserves sups 24 O—3.3
Lower adjoint, preserving compact elements 271 IV—1.11 272
Lower adjoint, preserving Scott open sets 268 IV—1.4
Lower adjoint, preserving the way-below relation 268 IV—1.4 271
Lower bound 1 O—1.1
Lower limit, of a net 133 II—1.1
Lower semicontinuous function 17 O—2.10 132
Lower semicontinuous function is Scott-continuous 159 II—2.3(3)
| Lower semicontinuous function, form a continuous lattice 64 I—1.22
Lower set 3 O—1.3
Lower topology 43 O—5.4 210
Lower topology is productive 211 III—1.3
Lower topology, continuous function for 210 III—1.2
Lower topology, open sets 238 III—3.28(i)
Meet 1 O—1.1
Meet continuous (semi)lattice 56 I—1.8
Meet continuous (semi)lattice, auxiliary relations on 59 I—1.14
Meet continuous (semi)lattice, is compact Hausdorff 224 III—2.15
Meet continuous (semi)lattice, is Hausdorff 222 III—2.9
Meet continuous (semi)lattice, is semitopological 221 III—2.8
Meet continuous (semi)lattice, is zero dimensional 224 III—2.16
Meet continuous (semi)lattice, Lawson topology has small semilattices 223 III—2.13 224
Meet continuous (semi)lattice, open filters are a basis for the Scott topology 223 III—2.13
Meet continuous (semi)lattice, order compatible topologies 154 II—1.34
Meet continuous (semi)lattice, Scott topology is a dual frame 206 II—4.28
Meet continuous (semi)lattice, way-below relation in 53 I—1.5(i)(3) 60
Meet continuous (semi)lattice, when a continuous (semi)lattice 60 I—1.16 224
Meet continuous (semi)lattice, when an algebraic (semi)lattice 224 III—2.16
Meet continuous (semi)lattice, with algebraic Scott topology 224 III—2.16
Meet continuous (semi)lattice, with continuous Scott topology 221 III—2.8 222 224
Meet continuous dcpo 219 III—2.1
Meet continuous dcpo, closed lower sets 221 III—2.5
Meet continuous dcpo, open upper sets 221 III—2.5
Meet continuous dcpo, when a domain 222 III—2.11
Meet continuous semilattice 36 O—4.1
Meet-continuous lattice 36 O—4.1
Meet-continuous lattice is a topological lattice in the Scott topology 498 VII—1.11
Meet-continuous lattice, closure properties of 40 O—4.8
Meet-continuous lattice, Scott topology on 198 II—4.17 199
Meet-continuous lattice, when a compact pospace 518 VII—4.4
Meet-continuous lattice, when a continuous lattice 74 I—1.35
Meet-continuous lattice, when locally strongly sober 497 VII—1.10
Meet-continuous lattice, when Scott topology is productive 498 VII—1.11
Meet-continuous lattice, with continuous Scott topology 199 II—4.18 518
Meet-continuous lattice, with join continuous Scott topology 198 II—4.17 199
Meet-irreducible element see “Irreducible element”
Minimal upper bound 253 III—5.3
Modular lattice 108 I—3.29
Modular law, for valuations 375 IV—9.1
Monogeneric subset 186 II—3.18
Monotone convergence space 183 II—3.12
Monotone convergence space, is a domain 184 II—3.16
Monotone function 5 O—1.9
Monotone net 2 O—1.2
Monotone normal pospace is embeddable in a cube 444 VI—1.16
mub-complete 253 III—5.3
Net 2 O—1.2
Net, antitone 2 O—1.2
Net, directed 2 O—1.2
Net, filtered 2 O—1.2
Net, lower limit of 133 II—1.1
Net, monotone 2 O—1.2
O-regular topology, for a poset 494 VII—1.6
Open filter, form a continuous semilattice (on a continuous semilattice) 145 II—1.17
Open filter, form a continuous semilattice (on a continuous semilattice), form a domain (on a domain) 145 II—1.17
Open filter, form a continuous semilattice (on a continuous semilattice), on a dcpo 95 I—3.1
Open filter, form a continuous semilattice (on a continuous semilattice), on a domain 96 I—3.3
Open function 269 Remarks preceding VI—1.6
Open upper set, in a dcpo 95 I—3.1
Open upper set, in a dcpo, maximal element in the complement 96 I—3.4
Operator, closure see “Closure operator”
Operator, closure, kernel see “Kernel operator”
Opposite relation 4 O—1.7
Order connected 471 VI—5.13
Order consistent topology 152 II—1.30 152 186
Order consistent topology on a poset 485 VI—6.30
Order convergence, of a net 217 remarks preceding III—1.17
Order preserving function 5 O—1.9
Order regular topology, for a poset 494 VII—1.6
Order topology 217 remarks preceding III—1.22 217
Order, auxiliary see “Auxiliary relation”
Order-compatible topology 154 II—1.34
Order-generating set, in a poset 97 I—3.8 97
Partial function 15 O—2.7(10)
Partial order, closed 440 VI—1.1
Partial order, closed, lower semiclosed 440 VI—1.1
Partial order, closed, semiclosed 253 III—5.1 440
Partial order, closed, upper semiclosed 440 VI—1.1
Partial order, closed, with closed graph 440 VI—1.1
Partially ordered set 4 O—1.6 (see also “4 Poset”)
Patch topology 44 O—5.10 419
Patch topology is functorial 489 VI—7.6
Patch topology on a compact coherent space 475 VI—6.5
Patch topology, on a domain 482 VI—6.24
Patch topology, on the primes is compact 420 V—5.13
Patch topology, on the primes is compact, is the Lawson topology 419 V—5.12
Plotkin powerdomain 364 IV—8.11 367 368
Plotkin powerdomain and the domain of lenses 370 IV—8.18
Plotkin powerdomain of an algebraic domain 373 IV—8.24
Point valuation 380 IV—9.9
Pointed dcpo 9 O—2.1
Polish space 45 O—5.13
Polish space, domain environment 434 V—6.6
POSET 4 O—1.6
Poset has an order consistent topology 494 VII—1.7
Poset, 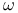 -point in 494 VII—1.6 -point in 494 VII—1.6
Poset, algebraic see “Algebraic poset”
Poset, as a category 23 remarks following O—3.1
Poset, bounded complete 9 O—2.1
Poset, continuous see “Continuous poset”
Poset, directed complete 9 O—2.1
Poset, o-regular topology for 494 VII—1.6
Poset, order convex hull of a subset 441 VI—1.5
Poset, order convex subset of 441 VI—1.5
Poset, order regular topology for 494 VII—1.6
Poset, radially convex metric for 445 VI—1.17
Poset, when each point is sup of 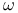 -points 494 VII—1.7(iii) -points 494 VII—1.7(iii)
Poset, with compatible topology 440 VI—1.2
Pospace 440 VI—1.1
Pospace is Hausdorff 441 VI—1.4
Pospace is locally order convex if compact 442 VI—1.9
Pospace is monotone normal if compact 442 VI—1.8
Pospace is semiclosed 440 remarks following VI—1.1
Pospace, arc chain in 469 VI—5.5
Pospace, compact see “Compact pospace”
Pospace, local minimum in 469 VI—5.8
Pospace, locally order convex 441 VI—1.5
Pospace, monotone normal 442 VI—1.7
Pospace, open upper sets, form, an o-regular topology 494 VII—1.7
Pospace, open upper sets, form, an o-regular topology, form, an order consistent topology 494 VII—1.7
Pospace, radially convex metric for 445 VI—1.17
Powerdomains 359 IV—8
Powerdomains, extended probabilistic 380 IV—9.7
Powerdomains, extended probabilistic, universal property 390 IV—9.24
Powerdomains, probabilistic 380 IV—9.7
Powerset of a set 13 O—2.7(1)
Powerset of a set, is an algebraic lattice 120 I—4.15(1)
Preorder 1 O—1.1
Preordered set 1 O—1.1
Priestley duality, for distributive arithmetic lattices 491 VI—7.10
Prime element 98 I—3.11 99
Prime element in a completely distributive lattice 398 V—1.7
Prime element is compactly prime 397 V—1.5
Prime element, in 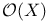 100 I—3.14 100 I—3.14
Prime element, in 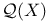 100 I—3.14 100 I—3.14
Prime element, order generate a continuous semilattice 99 I—3.13
Prime element, The Lemma 396 V—1.1
Prime filter 103 I—3.18
Prime filter in a power set 104 I—3.19
Prime ideal 103 I—3.18
Prime ideal in a distributive lattice 104 I—3.20
Prime ideal in a poset or semilattice 103 I—3.17
Prime ideal in C(X), closed, for X compact Hausdorff 399 V—1.12
Principal filter 3 O—1.3
Principal filter embedding, on a poset 16 O—2.8(4)
Principal ideal 3 O—1.3
Principal ideal embedding, on a poset 16 O—2.8(4)
Pro-complete category 331 IV—6.1
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
 |
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



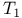 for complete (semi)lattices
for complete (semi)lattices  -point in
-point in