Авторизация
Поиск по указателям
Hovey M. — Model Categories, Vol. 63
Обсудите книгу на научном форуме Нашли опечатку?
Название: Model Categories, Vol. 63Автор: Hovey M. Аннотация: [The book] starts with an account of the definitions, and a development of the homotopy theory of model categories. This is probably the first time in which the important notion of cofibrant generation has appeared in a book, and the consideration of the 2-category of model categories and Quillen adjunctions is another interesting feature. — Bulletin of the London Mathematical Society Model categories are used as a tool for inverting certain maps in a category in a controllable manner. As such, they are useful in diverse areas of mathematics. The list of such areas is continually growing. This book is a comprehensive study of the relationship between a model category and its homotopy category. The author develops the theory of model categories, giving a careful development of the main examples. One highlight of the theory is a proof that the homotopy category of any model category is naturally a closed module over the homotopy category of simplicial sets. Little is required of the reader beyond some category theory and set theory, which makes the book accessible to advanced graduate students. The book begins with the basic theory of model categories and proceeds to a careful exposition of the main examples, using the theory of cofibrantly generated model categories. It then develops the general theory more fully, showing in particular that the homotopy category of any model category is a module over the homotopy category of simplicial sets, in an appropriate sense. This leads to a simplification and generalization of the loop and suspension functors in the homotopy category of a pointed model category. The book concludes with a discussion of the stable case, where the homotopy categoryis triangulated in a strong sense and has a set of small weak generators.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1998Количество страниц: 207Добавлена в каталог: 27.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
76 76 192 see also k-spaces pointed see also topological spaces compactly pointed see also simplicial category 75 see also cardinal see also lambda sequence 75 75 2-category 15 22 23 24—26 2-category of C-algebras 105 2-category of C-model categories 114 2-category of C-modules 104 2-category of categories 18 24 2-category of categories and adjunctions 24 2-category of central C-algebras 106 2-category of central monoidal C-algebras 115 2-category of closed monoidal categories 107 2-category of closed monoidal pre-triangulated categories 174 2-category of model categories 18 24 191 2-category of monoidal C-model categories 115 2-category of monoidal categories 103 2-category of monoidal model categories 113 2-category of pointed model categories 145 2-category of pre-triangulated categories 172 2-category of stable homotopy categories 184 2-category of stable model categories 176 2-category of symmetric C-algebras 105 2-category of symmetric monoidal C-algebras 115 2-category of symmetric monoidal categories 104 2-category of triangulated categories 176 2-category, model 191 194 2-functor 24 Acyclic chain complex see also chain complex acyclic Adjunction of two variables 106 116 119 Anodyne extension 79 80—83 109 Associativity isomorphism 134 Basepoint 4 Bimodules 102—103 106 Bisimplicial sets 128—129 131—132 Boundary map 87 88 156 170 Brown, Ken see also Ken Brown’s lemma C-algebra 104 C-algebra functor 104 C-algebra natural transformation 104 C-algebra structure 104 C-model category 101 114 118 C-module 104 C-module functor 104 C-module natural transformation 104 C-module structure 104 C-Quillen functor 114 Cardinal 28 Cardinal 29 Cardinality argument 45 Catad see also 2-category of Category of simplices of a simplicial set 75 124 Central C-algebra 105 Central C-algebra functor 106 Central monoidal C-model category 118 Ch(B) see also chain complexes of Ch(R) see also chain complexes of Chain complex, acyclic 41 Chain complexes of abelian groups 114 143—145 192 Chain complexes of comodules 28 60—72 112 114 176 188 194 Chain complexes of modules 27 40 41—48 111—112 114 176 183 188 194 Chain homotopy 43 Chain map 40 Closed 49 Closed monoidal category 106 Closed monoidal functor 106 Closed monoidal structure 106 Closed symmetric monoidal category 63 77 Cofiber 147 Cofiber sequence 147 151 156 157—165 169 177—182 Cofibrant 4 Cofibrant replacement functor 5 Cofibration 3 Cofibration, generating 34 Cofibration, trivial 3 Cofibration, trivial, generating 34 Cofinality of a cardinal 29 Cogroup object 151 Cogroup structure 150 151 Cogroup structure on 151 Cohomology functor 184 195 Colimit, homotopy 185 195 Colimit, sequential 185 195 Commutative monoid 192—193 Comodule 61 Comodule, cofree 63 Comodule, injective 63—65 Comodule, simple 61 Comodules 102 105 Comonad 193 Compactly closed 58 Compactly open 58 Correspondence of homotopies 150 Cosimplicial frame 127 128 130—139 144 167—169 Cosimplicial frames, map of 127 Cosimplicial identities 73 Cosimplicial object 73 76 Cosmall 34 Cotriple 193 Cube lemma 126 153 158 161 166 168 CW -complex 51 Cylinder object 8 9 127 152—153 Deformation retract 53 Degeneracy map 73 Degeneracy of a simplex 74 Degree function 124 Derived adjunction 18 Derived functor, total left 16 17—22 Derived functor, total right 16 Diagonal functor 128—129 131—132 Dimension of a simplex 73 Direct category 119 120 121—124 Dual model category 4 Duality 2-functor 24 107 115 118 122 126 127 170 173 Dwyer, Bill 1 119 Equivalence in a 2-category 24 Exact adjunction 172 181 F 81 108 Face map 73 Face of a simplex 74 Fiber 148 Fiber homotopy equivalence 89 90—91 Fiber sequence 147 151 156 157—165 169 177—182 Fibrant 4 Fibrant replacement functor 5 Fibration 3 Fibration, Kan 79 Fibration, locally trivial 89 92—93 95—97 Fibration, minimal 89 91 92—95 97 Fibration, trivial 3 finite 29 187 Framing 119 123 127 128—129 131—145 Franke, Jens 195 Frobenius ring 36 37—40 71—72 112 Frobenius ring, Noetherian 39 Function complex 128 Function complex of simplicial sets 77 Functor, monoidal see also monoidal functor Functorial factorization 2 15 16 28 Geometric realization 77 78—81 85 95—99 102 114 118 Geometric realization, preserves fibrations 97 Geometric realization, preserves finite limits 80 Geometric realization, preserves products 77 Goerss, Paul 193 Group object 151 Group ring 36 Group structure 151 Group structure on 151 Hirschhorn, Phil, x 1 Homology of a chain complex 41 Homotopic maps 9 Homotopy category 7 Homotopy equivalence 9 11 Homotopy groups of a chain complex of comodules 65 Homotopy groups of a fibrant simplicial set 83 85 86—89 97—99 Homotopy groups of a topological space 50 Homotopy of continuous maps 50 Homotopy of simplicial maps 86 Homotopy of vertices 84 Hopf algebra 36 60 112 Hopkins, Mike 193 Horizontal composition in a 2-category 23 Horizontal composition of natural transformations 18 23 Hurewicz cofibration 191 Hurewicz fibration 96 192 I-cell see also relative I-cell complex I-cell complex 31 I-cofibration 30 I-fibration 30 I-injective 30 I-projective 30 Inclusion of topological spaces 49 Injective model structure 44 112 Inverse category 119 120 121—124 Johnson, Mark x K see also k-spaces k-small 29 k-space 58 k-spaces 77 80 98 106 111 114 118 k-spaces, pointed 111 114 118 176 Kan, Dan x 1 3 119 194 Kelley space see also k-space Ken Brown’s lemma 6 11—12 14 131—132 136 Lambda sequence 28 Latching space 120 122 124 Left exact 172 Left homotopy 9 Left homotopy between right homotopies 149 Left lifting property 3 Lewis, Gaunce x Limit, homotopy 175 185 186 195 Linear extension 120 Localizing subcategory 184 195 Locally trivial fibration see also fibration locally Loop functor 148 149—174 176—177 179—183 Mapping cylinder 165 167 Mapping cylinder, double 165 Matching space 120 122 124 May, Peter 184 193 McClure, Jim 192 Minimal fibration see also fibration minimal MOD see also 2-category of Model category 3 Model category, cofibrantly generated 27 34 35—36 108—109 123 183 185 187 Model category, fibrantly generated 34 Model category, finitely generated 34 175 184 187—190 Model category, pointed 4 14 15 21 26 36 115 144—145 147—174 185—190 195 Model category, simplicial 101 114 119 128 136 138—139 142—145 194 Model category, simplicial, pointed 115 Model category, stable 175 176 185 194 Model structure 3 Model structure, product 4 7 14 19 Module over a monoidal category see also C-module Modules over a Frobenius ring 27 Monad 193 Monoidal C-model category 115 118 Monoidal C-Quillen functor 115 Monoidal category 101 102 Monoidal functor 102 Monoidal model category 101 109 110—119 140—145 Monoidal model category, pointed 145 173—174 Monoidal model category, stable 176 Monoidal model category, symmetric 110—118 Monoidal natural transformation 103 Monoidal Quillen adjunction 113 Monoidal Quillen functor 113 141 Monoidal structure 102 Natural transformation, monoidal see also monoidal natural transformation Natural transformation, total derived 16 18 22 Non-degenerate, simplex 74 Octahedral axiom 160—161 170 177 Operads 193 Ordinal 28 120 p-related vertices 91 93 Palmieri, John x Paracompact 96 Path component of a simplicial set 85 Path object 8 9 Pre-triangulated category 147 169 170 171—174 183 194 Pre-triangulated category, closed central monoidal 173 Pre-triangulated category, closed monoidal 173 174 Pre-triangulated category, closed symmetric monoidal 173 Pre-triangulation 169 170 Pseudo-2-functor 18 22 24 101 115 117—118 136 138 140—141 143 145 173—174 184 195 Pseudo-2-functor, homotopy 25 Pseudo-2-functor, natural isomorphism of 137 Pushout product 108 109 q see also cofibrant replacement functor Quillen adjunction 14 15—22 35 71 131 136—139 163 191 Quillen adjunction of two variables 107 Quillen bifunctor 108 109—116 Quillen equivalence 13 19 20—22 26 48 98 191 Quillen functor 35 48 123 128 163—165 Quillen functor, left 13 14—19 Quillen functor, monoidal see also monoidal Quillen functor Quillen functor, right 14 15—19 Quillen, Daniel 1—195 R see also fibrant replacement functor Reedy category 119 123 124 125—127 195 Reedy model structure 126 127 130 133 144 167 Reedy scheme 195 reflect 21 Relative I-cell complex 30 31—36 Retract argument 5 Rezk, Charles, x 191 193 Right exact 172 Right homotopy 9 Right homotopy between right homotopies 149 Right lifting property 3 Right proper 57 S-modules 113 176 184 Schwede, Stefan 49 109 194 Serre fibration 51 96 97 Shipley, Brooke x Sierpinski space 49 Simplicial category 73 119 123—125 Simplicial frame 127 128 130—133 144 163 Simplicial frames, map of 127 Simplicial identities 74 Simplicial object 73 Simplicial set, finite 74 Simplicial sets 73 74—101 109 114 118 119 128—145 188 192 Simplicial sets, pointed 98 100 110 114 118 176 183 185—187 Singular functor 77 98 Small 29 175 183 187—190 Small object argument 28 32 187 Smith, Jeff x 107 109 SSET see also simplicial sets SSet see also simplicial sets pointed Stable category of modules 37 Stable equivalence of modules 36 Stable homotopy category 195 Stable homotopy category, algebraic 175 184
Реклама
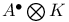
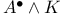
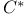-algebras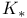 
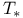
![$\Delta[n]$](/math_tex/c6bbbc697db67e4917f7a4b0e3ff723b82.gif)
-filtered cardinal 
-sequence ![$\Lambda^r [n]$](/math_tex/726b238e25defb7b32aa209e5b144dcb82.gif)
![$\partial \Delta [n]$](/math_tex/1382f83389d6b8053b9fcdc89340b92982.gif)
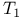inclusion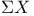 
g 
|
|
О проекте