|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cabanes M., Enguehard M., Bollobas B. (Ed) — Representation Theory of Finite Reductive Groups (New Mathematical Monographs Series), Vol. 1 |
|
|
 |
| Предметный указатель |
 , a scalar product xvii , a scalar product xvii
 , l-modular splitting system 75 , l-modular splitting system 75
 59 59
$(\mathcal{O}, K, k), l-modular splitting system xvii
 , Harish — Chandra restriction 47 , Harish — Chandra restriction 47
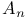 , ,  , , 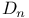 , (types of Coxeter groups) 24 , (types of Coxeter groups) 24
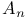 , , 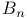 , , 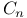 , , 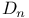 , E, , E, 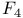 , ,  , (types of crystallographic root systems) 119 , (types of crystallographic root systems) 119
 , ( , ( 90 90
 , ( , ( , standard basis element of Hecke algebra 41 44 , standard basis element of Hecke algebra 41 44
 morphism between induced cuspidal triples 8 morphism between induced cuspidal triples 8
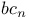 24 24
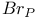 , Brauer morphism 76 , Brauer morphism 76
 , ,  , block, or block idempotent, of G acting by Id on the indecomposable module M 77 , block, or block idempotent, of G acting by Id on the indecomposable module M 77
 , block of G not annihilated by , block of G not annihilated by  75 75
 , sum of l-block idempotents defined by , sum of l-block idempotents defined by  134 134
 30 30
 , ,  , (B in a BN-pair, , (B in a BN-pair,  , ,  , subgroups of B 30 , subgroups of B 30
![$C \mapsto C[n]$](/math_tex/88789b92c44ea316e2225658491c739c82.gif) , ( , ( shift on complex C 57 375 shift on complex C 57 375
$C((M_{\sigma}, f_{\sigma}^{\sigma})) 58
 , ,  240 320 240 320
 , ( , ( a set of subquotients), set of cuspidal triples 7 a set of subquotients), set of cuspidal triples 7
 , the connected centralizer of g in G 393 , the connected centralizer of g in G 393
 , categories of complexes on the abelian category , categories of complexes on the abelian category  375 375
 , centralizer of X in H xv , centralizer of X in H xv
 , decomposition matrix of the A-module M 84 , decomposition matrix of the A-module M 84
 , degree of the simplex , degree of the simplex  58 58
 381 381
 , ,  , generalized decomposition map for , generalized decomposition map for  74 77 74 77
 , derived categories of the abelian category A 377 , derived categories of the abelian category A 377
 subcategory of subcategory of  407 407
 , ,  , with , with  , sets of distinguished elements of W 24 , sets of distinguished elements of W 24
 , duality functor 67 , duality functor 67
 KG^F$ 134 KG^F$ 134
 , central primitive idempotent of K G for , central primitive idempotent of K G for  132 132
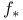 , , 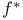 , direct and inverse images 383 399 406 , direct and inverse images 383 399 406
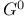 393 393
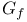 , ,  , subgroups of , subgroups of  348 348
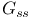 393 393
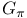 , , 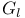 , set of , set of  - or l-elements xv - or l-elements xv
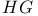 , H is a normal subgroup of G xv , H is a normal subgroup of G xv
 , i-th cohomology group of a cochain complex C 376 , i-th cohomology group of a cochain complex C 376
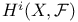 , ( , ( a sheaf on a sheaf on 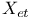 ), ith cohomology group of a sheaf 385 ), ith cohomology group of a sheaf 385
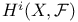 , ( , ( a sheaf on a sheaf on 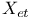 ), ith cohomology group with compact support 409 ), ith cohomology group with compact support 409
 , i-th homology group of a chain complex C 57 , i-th homology group of a chain complex C 57
 322 322
 , induction from a subalgebra 289 , induction from a subalgebra 289
 , induction from a subquotient 3 , induction from a subquotient 3
 , induction from a subgroup xvi , induction from a subgroup xvi
 378 378
 112 112
 168 168
 , homotopic category 376 , homotopic category 376
 , Levi subgroup defined by , Levi subgroup defined by 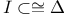 32 32
 , matrix algebra xvi , matrix algebra xvi
 , constant sheaf associated with X 406 , constant sheaf associated with X 406
 322 322
 , normalizer of X in a group H xv , normalizer of X in a group H xv
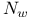 , with , with 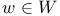 , a map , a map  123 123
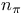 , the , the  -part of integer n xv -part of integer n xv
$part(\pi-) xv
 132 132
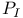 , parabolic subgroup defined by , parabolic subgroup defined by  28 28
 , polynomial order 190 , polynomial order 190
 , regular character of G 132 , regular character of G 132
 , restriction to a subquotient 5 , restriction to a subquotient 5
 , restriction to a subgroup xvi , restriction to a subgroup xvi
 , ,  409 409
 , Harish — Chandra induction for L a Levi subgroup of G 47 , Harish — Chandra induction for L a Levi subgroup of G 47
 , Deligne — Lusztig character 126 , Deligne — Lusztig character 126
 , direct image with compact support 408 , direct image with compact support 408
 , twisted induction of blocks 337 , twisted induction of blocks 337
 394 394
 125 125
 , Deligne-Lusztig twisted induction 125 , Deligne-Lusztig twisted induction 125
 405 405
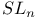 28 28
 29 222 29 222
$SO_{n,v} (v = 0, w 1 d)$
 228 228
 38 38
 , the Steinberg module or character 301 , the Steinberg module or character 301
 177 177
 150 150
 (q-Schur algebra) 326 (q-Schur algebra) 326
 , relative trace 76 , relative trace 76
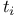 279 279
 , a semi-direct product xv , a semi-direct product xv
 , a subgroup of U, defined by , a subgroup of U, defined by  30 30
 , where , where  and and  26 47 48 26 47 48
 281 281
 , a subgroup of W, defined by , a subgroup of W, defined by  23 23
 , with , with  26 26
 , 281 , 281
 , with , with  a linear character of a linear character of  149 168 149 168
$X\stackrel{w}{\longrightarrow}Y 146
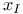 , ( , ( ) 273 ) 273
 , ,  , subvariety of G/P 110 , subvariety of G/P 110
$X_{et}, the etale topology on X 404
 147 147
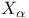 , ,  root 30 root 30
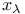 276 276
 322 322
 273 273
 , ,  , subvariety of G/V 110 , subvariety of G/V 110
 147 147
![$Y_{[v,w]}$](/math_tex/89416990847c08eeaf1d9cc1cc73bf3c82.gif) 162 162
 276 276
 112 112
 78 78
 -set 78 -set 78
 , ,  a partition 78 a partition 78
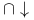 , non-symmetric intersection of subquotients 6 , non-symmetric intersection of subquotients 6
 59 59
 , (C a complex of A-modules), Lefschetz character 381 , (C a complex of A-modules), Lefschetz character 381
 , a set of simple roots in , a set of simple roots in  , in bijection with S 23 , in bijection with S 23
 135 135
 91 91
 79 79
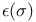 78 78
 , a sign 126 , a sign 126
 285 285
 162 162
 382 382
 , ,  , Gelfand — Graev module 301 , Gelfand — Graev module 301
 , dual partition 276 , dual partition 276
 -regular set of subquotients 6 -regular set of subquotients 6
 314 314
 276 276
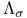 322 322
 391 391
 418 418
 , , 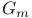 , additive and multiplicative algebraic groups 393 , additive and multiplicative algebraic groups 393
 391 391
 413 413
 (s a semi-simple rational element in G*), a rational series 127 (s a semi-simple rational element in G*), a rational series 127
 18 18
 , a union of rational series (and of blocks) 133 , a union of rational series (and of blocks) 133
$](/math_tex/44c93ecce47199e899c80bd8a735039282.gif) 168 168
 , sheafification of a presheaf 383 405 , sheafification of a presheaf 383 405
 150 150
 88 88
 279 279
 44 44
 , Hecke algebra with parameters , Hecke algebra with parameters  44 44
 \mathcal{O}}(\mathfrak{C}n, q)$ 275 \mathcal{O}}(\mathfrak{C}n, q)$ 275
 322 322
 , Levi system of subquotients 32 , Levi system of subquotients 32
 , (M a G-module, X/G a quotient variety), a coherent , (M a G-module, X/G a quotient variety), a coherent  -module 400 -module 400
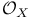 , structure sheaf of a scheme 390 , structure sheaf of a scheme 390
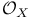 -module 399 -module 399
|  177 177
 , tangent map at x 392 , tangent map at x 392
 , (X a variety), tangent sheaf 392 , (X a variety), tangent sheaf 392
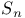 23 23
 78 78
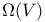 228 228
 219 219
 , left derived tensor product 381 , left derived tensor product 381
 , ,  , ,  23 23
 -subgroup 190 -subgroup 190
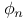 , cyclotomic polynomial xvi , cyclotomic polynomial xvi
 , 24 , 24
 -regular element xv -regular element xv
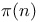 , ,  , numbers of partitions 309 , numbers of partitions 309
 , , 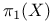 , fundamental group 416 , fundamental group 416
 , tame fundamental group with respect to D 417 , tame fundamental group with respect to D 417
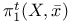 , tame fundamental group 416 , tame fundamental group 416
 , ,  281 281
 91 91
 , ,  , ,  149 149
 (s a semi-simple rational element in G*), a geometric series 127 (s a semi-simple rational element in G*), a geometric series 127
(q-)Schur algebra 298
(W, S), a Coxeter system 23
4\RHO_{c, d}(\lambda)$ 309
A — Mod, A — mod, module categories xvi
A(t) 214
Abelian defect conjecture (Broue) 369
Abelian, additive categories 374
Acyclic 376
Alperin’s “weight” conjecture 96
Ariki-Koike 296
B(s) 214
Base change 398
Base change for a proper morphism 408
Basic set of characters 201
Bi-functor 380
Bi-partition 330
Bi-projective 57
Bimodule xvi
Block (l-), l-block idempotent (l a prime number) 75
BN-pair 27
BN-pair, split, of characteristic p 30
BN-pair, strongly split, 30
Bonnafe — Rouquier’s theorem 141
Borel subgroup 394
Brauer morphism 76
Brauer’s “second Main Theorem” and “third Main Theorem” 77
Broue — Michel’s theorem 131
Broue’s abelian defect conjecture 369
Building 40
CF(G, A), space of central functions from G to A xvii
CF(G, K, B), CF(G, B), space of central functions defined by the block B of G 75
CL(V), Clifford group 228
Coefficient system 58
Coherent sheaf 399
Compact support, cohomology with, direct image with 408
Compactification 408
Complex, acyclic 57 376
Complex, bounded 57
Complex, perfect 381
Complex, tensor product of,s 57
Composition of an integer,  308 308
Cone(f) 375
Conformal groups 240
Control subgroup 363
Core 79
CSP 320
Cuspidal module, triple 7
Dade’s conjectures 100
DC, duality complex 64
Dec(A), decomposition matrix of the algebra A 84
Decomposition matrix 84
Defect, central 77
Defect, zero 77
Degenerate symbols 216
Deligne — Lusztig xii
Derived categories 377
Derived functors 379
Dimension of a point 398
Dimension of a variety 391
Dipper — Du 298
Dipper — James 271
Divisor, smooth 392
Divisor, smooth, with normal crossings 392
Donovan’s conjecture 370
Duality, Alvis — Curtis 67
Duality, local 420
Duality, Poincare — Verdier 412
e(V), idempotent defined by the subgroup V 5
e-cuspidal, E-cuspidal 335
Equivalence relation between subquotients 6
Equivalence, derived 57
Equivalence, Morita 137
Etale, covering 405
Etale, morphism 404
Etale, neighborhood 405
Etale, topology 404
F, an algebraic closure of the field 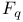 103 103
F, an endomorphism of G 104 121 395
Fibered product 398
Fong-Srinivasan xii
Frobenius, algebra 12
Frobenius, morphism 395
F[ V], regular functions on an F-variety V 389
G*, a group in duality with G 123
G,  , ,  , a connected reductive group over F, the associated adjoint and simply connected groups 394 , a connected reductive group over F, the associated adjoint and simply connected groups 394
Galois covering 416
Geck — Hiss — Malle 298
Generic block 358
GL xvi
Global sections 382
Global sections, generated by 400
Grothendieck xii 55 101 102 373 388 396 403 404 416
Group, 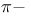 xv xv
Group, algebraic 393
Group, defect 76
Group, F- 393
Group, finite reductive xiii
Group, fundamental, tame fundamental 416
Group, Grothendieck 173
Group, reductive 394
Gruber — Hiss 318
GUn 29
H or  15 298 15 298
Haastert 117
Harish-Chandra 40
hd(M), head of a module xvi
Hecke algebra 2 4 44
Henselian 411
Hoefsmit’s matrices 279
Hom 385 399
Homgr 376
Homotopic category 376
Hook 78
I(v, w) 162
IBr(G), set of irreducible Brauer characters 299
Immersion 398
ind(w), ( , index 42 , index 42
Induction, Harish-Chandra 1
Induction, twisted (or Deligne — Lusztig) 125
Intersect transversally 392
Irr(G), set of irreducible characters xvii
Irr(G, b), subset of Irr(G) defined by a block idempotent b of G 75 132
J(A), Jacobson radical of A xvi
Jordan decomposition of elements in G 393
Jordan decomposition of irreducible representations of 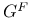 209 209
Kunneth formula 412
l(w), length of with respect to S 397 with respect to S 397
l-adic sheaf, l-adic cohomology 409
l-modular splitting system xvii
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 , a scalar product
, a scalar product  , l-modular splitting system
, l-modular splitting system 
 , Harish — Chandra restriction
, Harish — Chandra restriction 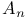 ,
,  ,
, 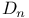 , (types of Coxeter groups)
, (types of Coxeter groups) 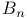 ,
, 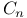 ,
, 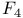 ,
,  , (types of crystallographic root systems)
, (types of crystallographic root systems)  , (
, (
 , (
, ( , standard basis element of Hecke algebra
, standard basis element of Hecke algebra  morphism between induced cuspidal triples
morphism between induced cuspidal triples 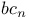
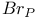 , Brauer morphism
, Brauer morphism  ,
,  , block, or block idempotent, of G acting by Id on the indecomposable module M
, block, or block idempotent, of G acting by Id on the indecomposable module M  , block of G not annihilated by
, block of G not annihilated by 
 , sum of l-block idempotents defined by
, sum of l-block idempotents defined by 

 ,
,  , (B in a BN-pair,
, (B in a BN-pair,  ,
,  , subgroups of B
, subgroups of B ![$C \mapsto C[n]$](/math_tex/88789b92c44ea316e2225658491c739c82.gif) , (
, ( shift on complex C
shift on complex C  ,
, 
 , (
, ( a set of subquotients), set of cuspidal triples
a set of subquotients), set of cuspidal triples  , the connected centralizer of g in G
, the connected centralizer of g in G  , categories of complexes on the abelian category
, categories of complexes on the abelian category 
 , centralizer of X in H
, centralizer of X in H  , decomposition matrix of the A-module M
, decomposition matrix of the A-module M  , degree of the simplex
, degree of the simplex 

 ,
,  , generalized decomposition map for
, generalized decomposition map for 
 , derived categories of the abelian category A
, derived categories of the abelian category A  subcategory of
subcategory of 
 ,
,  , with
, with  , sets of distinguished elements of W
, sets of distinguished elements of W  , duality functor
, duality functor  KG^F$
KG^F$  , central primitive idempotent of K G for
, central primitive idempotent of K G for 
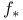 ,
, 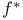 , direct and inverse images
, direct and inverse images 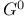
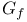 ,
,  , subgroups of
, subgroups of 
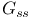
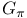 ,
, 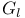 , set of
, set of  - or l-elements
- or l-elements 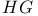 , H is a normal subgroup of G
, H is a normal subgroup of G  , i-th cohomology group of a cochain complex C
, i-th cohomology group of a cochain complex C 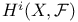 , (
, ( a sheaf on
a sheaf on 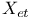 ), ith cohomology group of a sheaf
), ith cohomology group of a sheaf  , i-th homology group of a chain complex C
, i-th homology group of a chain complex C 
 , induction from a subalgebra
, induction from a subalgebra  , induction from a subquotient
, induction from a subquotient  , induction from a subgroup
, induction from a subgroup 


 , homotopic category
, homotopic category  , Levi subgroup defined by
, Levi subgroup defined by 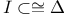
 , matrix algebra
, matrix algebra  , constant sheaf associated with X
, constant sheaf associated with X 
 , normalizer of X in a group H
, normalizer of X in a group H 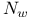 , with
, with 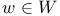 , a map
, a map 
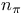 , the
, the 
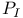 , parabolic subgroup defined by
, parabolic subgroup defined by 
 , polynomial order
, polynomial order  , regular character of G
, regular character of G  , restriction to a subquotient
, restriction to a subquotient  , restriction to a subgroup
, restriction to a subgroup  ,
, 
 , Harish — Chandra induction for L a Levi subgroup of G
, Harish — Chandra induction for L a Levi subgroup of G  , Deligne — Lusztig character
, Deligne — Lusztig character  , direct image with compact support
, direct image with compact support  , twisted induction of blocks
, twisted induction of blocks 

 , Deligne-Lusztig twisted induction
, Deligne-Lusztig twisted induction 
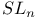



 , the Steinberg module or character
, the Steinberg module or character 

 (q-Schur algebra)
(q-Schur algebra)  , relative trace
, relative trace 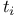
 , a semi-direct product
, a semi-direct product  , a subgroup of U, defined by
, a subgroup of U, defined by 
 , where
, where  and
and 

 , a subgroup of W, defined by
, a subgroup of W, defined by  , with
, with  ,
,  , with
, with  a linear character of
a linear character of 
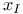 , (
, ( )
)  ,
,  , subvariety of G/P
, subvariety of G/P 
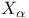 ,
,  root
root 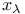


 ,
,  , subvariety of G/V
, subvariety of G/V 
![$Y_{[v,w]}$](/math_tex/89416990847c08eeaf1d9cc1cc73bf3c82.gif)



 -set
-set  ,
,  a partition
a partition 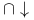 , non-symmetric intersection of subquotients
, non-symmetric intersection of subquotients 
 , (C a complex of A-modules), Lefschetz character
, (C a complex of A-modules), Lefschetz character  , a set of simple roots in
, a set of simple roots in  , in bijection with S
, in bijection with S 


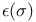
 , a sign
, a sign 


 ,
,  , Gelfand — Graev module
, Gelfand — Graev module  , dual partition
, dual partition  -regular set of subquotients
-regular set of subquotients 

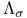


 ,
, 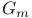 , additive and multiplicative algebraic groups
, additive and multiplicative algebraic groups 

 (s a semi-simple rational element in G*), a rational series
(s a semi-simple rational element in G*), a rational series 
$](/math_tex/44c93ecce47199e899c80bd8a735039282.gif)
 , sheafification of a presheaf
, sheafification of a presheaf 



 , Hecke algebra with parameters
, Hecke algebra with parameters 
 \mathcal{O}}(\mathfrak{C}n, q)$
\mathcal{O}}(\mathfrak{C}n, q)$ 
 , (M a G-module, X/G a quotient variety), a coherent
, (M a G-module, X/G a quotient variety), a coherent  -module
-module 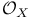 , structure sheaf of a scheme
, structure sheaf of a scheme 
 , tangent map at x
, tangent map at x  , (X a variety), tangent sheaf
, (X a variety), tangent sheaf 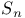

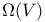

 , left derived tensor product
, left derived tensor product  ,
, 
 -subgroup
-subgroup 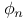 , cyclotomic polynomial
, cyclotomic polynomial  ,
, 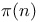 ,
,  , numbers of partitions
, numbers of partitions  ,
, 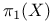 , fundamental group
, fundamental group  , tame fundamental group with respect to D
, tame fundamental group with respect to D 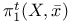 , tame fundamental group
, tame fundamental group  ,
, 

 ,
,  ,
, 
 (s a semi-simple rational element in G*), a geometric series
(s a semi-simple rational element in G*), a geometric series 
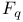
 ,
,  , a connected reductive group over F, the associated adjoint and simply connected groups
, a connected reductive group over F, the associated adjoint and simply connected groups 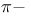

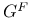
 with respect to S
with respect to S