|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Cabanes M., Enguehard M., Bollobas B. (Ed) — Representation Theory of Finite Reductive Groups (New Mathematical Monographs Series), Vol. 1 |
|
|
 |
| Предметный указатель |
l-modular, xvii 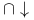 -stable 6 -stable 6
Lan, the Lang map 103
Lang’s map, theorem 104
Levi decomposition, Levi subgroup 394
Lie algebra of G 393
Local structure, information 360
Locally closed subvariety 391
Lusztig xii
Mapping cone 375
Max(A), affine variety associated with A 389
Morphism of varieties or schemes of finite type 398
Morphism of varieties or schemes, compactifiable 408
Morphism of varieties or schemes, dominant 396
Morphism of varieties or schemes, etale 404
Morphism of varieties or schemes, finite 395
Morphism of varieties or schemes, flat 404
Morphism of varieties or schemes, proper 399
Morphism of varieties or schemes, quasi-finite 395
Morphism of varieties or schemes, separable 396
Morphism of varieties or schemes, separated 398
Normalization 396
Null homotopic 376
O(w) 397
Open-closed exact sequence 411
Order on simplicial scheme 58
Order, Bruhat 397
Order, lexicographic 292
Order, local 172
Order, polynomial 119
Partition of an integer,  78 78
Perfect complex 381
Perfect isometry 139
Point, closed, generic, geometric 398
Polynomial order 190
Presheaf 382
Primes, bad 193
Primes, good 193
Principal block 77
Proj 386
Projection formula 412
Puig’s conjecture 370
Purity (cohomological) 413
Purity of branch locus 396
Quasi-affinity criterion 401
Quasi-isomorphism 57 376
Ramification 417 418
Regular linear character of U 301
Regular variety 392
RF, right derived functor 379
RHom 381
Root datum, root system 119 394
Scheme 397
Sh(X),  383 383
Sheaf 383
Sheaf over X 399
Sheaf, ample (coherent) 400
Sheaf, coherent 400
Sheaf, constant 383 406
Sheaf, constructible 406
Sheaf, dual 406
Sheaf, etale 405
Sheaf, generated by its local sections 400
Sheaf, locally constant 384 406
Sheaf, tensor product of 385
Sheaf, torsion 405
Sheaf, very ample 400
Sheafification, 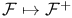 383 405 383 405
Simplex, simplicial scheme 57
Size of a partition 78
| Smooth 392
soc(M) xvi
Spec(A) 397
Split Levi subgroup (E-) 190
Splitting system xvi
Stalk 382 405 411
Standard tableaux 279
Steinberg module 95 301
Strict henselization,  411 411
Subgroup,  190 190
Subgroup, Borel 394
Subgroup, Levi 394
Subgroup, parabolic 28
Subpair, inclusion 76
Subpair, maximal 76
Subpair, self-centralizing 352
Subpair, “connected” 334
Subquotient 3
Subscript notation with variable symbols, 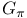 , ,  -elements of a group G xv -elements of a group G xv
Subscript notation with variable symbols,  , constant sheaf on X with stalk M 383 , constant sheaf on X with stalk M 383
Subscript notation with variable symbols, 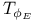 , (T a torus, E a set of integers), maximal , (T a torus, E a set of integers), maximal  -subgroup of T 191 -subgroup of T 191
Subscript notation with variable symbols, 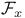 , stalk at a point 382 , stalk at a point 382
Subscript notation with variable symbols,  , stalk at a geometric point 405 , stalk at a geometric point 405
Symmetric algebra 12
S[v, w] 164
T, a torus 394
Tangent map, tangent sheaf 392
Tensor product of sheaves 399 406
Tits system 27
Torus 394
Triangle (distinguished) 378
Triangulated category 382
Triangulation 58
Twin characters 216
Twisted induction 125
Twisted inverse image  413 413
TYPE 121
T[v, w] 164
Uniform function 126 133
Unipotent block 135
Unipotent irreducible character 127
Unipotent radical 394
Variety, (quasi-)projective 391
Variety, affine 389
Variety, complete 391
Variety, defined over 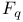 395 395
Variety, Deligne — Lusztig 110
Variety, G-quotient 396
Variety, interval 166
Variety, irreducible 391
Variety, normal 396
Variety, quasi-affine 391
Variety, regular 392
Variety, Schubert 397
Variety, smooth 392
Vector bundle 401
vinvertible (coherent) 400
X(w), subvariety of G/B 111 146
X[v, w] 166
Y(w), with 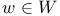 , subvariety of G/U 111 146 , subvariety of G/U 111 146
Young diagrams, tableaux 279
Y[v, w] 166
Z(H), center of the group H xv
Zariski — Nagata 396
Zariski, topology 390
Zariski’s main theorem 396
[a, b], a commutator xv
|G : H|, index of H in G xv
|X|, cardinality of the set X xv
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



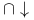 -stable
-stable 

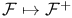


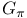 ,
,  -elements of a group G
-elements of a group G , constant sheaf on X with stalk M
, constant sheaf on X with stalk M 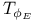 , (T a torus, E a set of integers), maximal
, (T a torus, E a set of integers), maximal  -subgroup of T
-subgroup of T 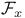 , stalk at a point
, stalk at a point  , stalk at a geometric point
, stalk at a geometric point 
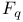
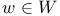 , subvariety of G/U
, subvariety of G/U