|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Street R., Murray M. (Ed), Broadbridge Ph. (Ed) — Quantum Groups: A Path to Current Algebra |
|
|
 |
| Предметный указатель |
Linearly independent 14
Mac Lane, coherence theorem 68 109
Mac Lane, Saundcrs 109 113
Manin, Yuri I. 10 64 65
McCrudden, Paddy xvi
Module, Cauchy 21
Module, finitely generated 13
Module, from R to S 16
Module, left R-module 13
Module, morphism 14
Module, projective 21
Module, right R-modute 13
Monoid 2 7 97
Monoid, affine over k 7
Monoid, arrow 97
Monoid, category 100
Monoid, commutative 3
Monoid, diagrammatic definition 7
Monoid, homomorphism 3
Monoid, morphism 3
Monoid, morphisms preserve invertibility 4
Monoid, quasi-Hopf 105
Monoid, R-atgebra 29
Monoidal category, tensor category 67
Monoidal functor, tensor functor 85
Moore, Ross, LATEX2HTML xvii
Moore, Ross, XY-pic xvi
Morita Theory 62
Morita Theory, fundamental theorem 22
Morphism of bialgebras 44
Morphism of C*-algebras 5
Morphism of coalgebras 38
Morphism of k-algebras 4 6
Morphism of Lie algebras 33
Morphism of monoids 3
Morphism of R-algebras 27
Morphism of rigs 4
Morphism, algebra 5
Morphism, comodule 62
Morphism, composable xii
Morphism, composite xii
Morphism, evaluation 19
Morphism, identity xii
Morphism, invertible xiii
Morphism, left inverse xiii
Morphism, map of varieties 6
Morphism, module morphism 14
Morphism, retraction 21
Morphism, right inverse xiii
Morphisms xi
Multilinear function 17
Multiplication, opposite 13
Multiplication, scalar 13
Multiplicative matrices 64
Natural famity 68
Natural isomorphism xiv
Natural numbers 4
Natural numbers, example of a rig 4
Natural transformation xiv 102
Naturality xiv
Non-com mutating indeterminates 9
Object of category 6
Object, coterminal xiii
Object, initial xiii
Object, representing xiv
Object, terminal xiii 7
Object, unit, 67
Objects xi
Opposite algebra 30
Opposite category xii
Opposite multiplication 13
Opposite, dual xii
Pasted composite 100
Pasting 99
Pasting, 2-cells 97
Planck constant 9
Poincare — Birkhoff — Witt 35
Point 5 6
Point as algebra morphism 5
Point of a k-algebra 6
Point, B-point 6
Point, B-point of a k-algebra 6
Primitive element in a coalgebra 41
Product in category X 6
Product of modules 24
Product of objects xii
Product, tensor 67
Product, tensor product 7
Projection xii 24
Projection, universal property xii
Projective 21
Projective plane xi
Projective plane, axioms xi
Projective plane, incidence xi
Projective plane, reverse 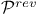 xi xi
QIST 10
Quadratic algebra 80
Quadratic algebra, category QA 80
Quadratic algebra, morphism 80
Quantization 9
Quantization, deforming commutative algebras to non-commutative ones 9
Quantum deformation 57
Quantum determinant 57
Quantum group 108 115
Quantum group over R 108
Quantum group, cotortile bimonoid in 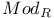 108 108
Quantum inverse scattering transform 10
Quantum matrices 9
Quantum plane 10 80
Quantum spaces 9
Quantum spaces, correspond to k-algebras 9
Quantum special linear group 12
Quantum superplane 10 81
Quantum, Cramer Rule 120
Quantum, general linear group 12 57
Quasi-bimonoid 104
Quasi-bimonoid in V 104
Quasitriangular bialgebra 72
R-algebra 27
R-algebra, commutative 30
R-algebra, group 29
R-algebra, monoid 29
R-algebra, skew commutative 31
R-algebra, symmetric 30
R-coalgebra 117
R-Lie algebra 32
R-module, derivation 32
R-module, two-sided 29
Representable functor xiv
Representation 29
| Representation of group on monoid 29
Representation, appropriate 109
Representing object xiv
Restriction of scalars 59 101
retract 21
Retraction morphism 21
Reverse-arrow universal property 63
Ribbons tangles 84
Ribbons YB-operator 88
Rig 4
Rig, commutative 4
Rig, morphism 4
Rig, natural numbers 4
Right inverse xiii
Ring 4
Ring with opposite multiplication 13
Rivano see Saavedra Rivano
Saavedra Rivano, Neantro 109
Sabadini, Nicoletta 117
Scalar multiplication 4
Self-adjoint 54
Set-like element in a coalgebra 40
Shum Mei Chee 84 91
Signed seta 83
Skew commutative 31
Small sets 86
Source of a tangle 83
Space seen from the other side of your brain 5
span 13
Strict 104
Strong monoidal functor tensor functor 85
Submodule 14
Submodule, generated by a subset 15
Supergeometry 10
Sweedler, Moss E. 115
switch 3 70
Symmetric R- algebra 30
Symmetric tensor category 69 79
Symmetry for a tensor category 68
TaEent, Ross xvi
Taking off your belt 91
Tangle 83
Tangle, autonomous braided category 83
Tangle, geometric 82
Tangle, source 83
Tangle, tangles on ribbons 84
Tangle, tangles on strings 82
Tangle, target 82
Tannaka duality 115 117
Tannaka duality theorem 109
Target of a tangle 82 83
Target, codomain xii
Tensor algebra 28
Tensor category 67 104
Tensor category, autonomous 84
Tensor category, balanced 73
Tensor category, braided 68
Tensor category, closed 78
Tensor category, free autonomous 117
Tensor category, left autonomous 117
Tensor category, opposite 68
Tensor category, strict 68 70 104
Tensor category, symmetric 69
Tensor functor 85
Tensor functor takes YB-operator into YB-operator 89
Tensor functor, balanced 86 114;
Tensor functor, braided 85; 114
Tensor functor, closed 86
Tensor functor, left-closed 86
Tensor functor, monoidal functor 85
Tensor functor, preserves dualizability 90
Tensor functor, preserves duals 86
Tensor functor, preserves products 87
Tensor functor, right-closed 86
Tensor functor, strict 85
Tensor functor, strong monoidal functor 85
Tensor functor, symmetric 86
Tensor functor, weak 85
Tensor object 104
Tensor product 67
Tensor product as composition of modules 16
Tensor product of braids 69
Tensor product of R-modules 29
Tensor product, multiple 16
Tensor product, represent bilinear function as module morphism 18
Tensor-horn 61
Terminal object xiii 7
Tortile 82 84
Twist 73 84
Twist element 75
Two-sided R-module 29
Ulbrich, Karl-Heinz 114
UNIT 81
Unit, left 67
Unit, object 67
Unit, right 67
Universal algebra 87
Universal enveloping algebra 33 40 46 87
Universal enveloping algebra is a cocommutative bialgebra 45
Universal property x
Universal property for internal horn 78
Universal property, end 110
Universal property, internal horn 110
Universal property, reverse-arrow 63
Universal, property 115
Up to coherent isomorphism 87
Vaughan, Elaine xvi
Vector space over R 13
Verity, Dominic R. 117
Walsh, Grahame xvii see
Walters, Robert F.G. 117
Weak, tensor functor takes monoids to monords 101
Weak, tensor functor, essentially 103
Whisker 98—100
Williams, Sam xvi
XY-pic, Kristoffer Rose xvi
XY-pic, Ross Moore xvi
Yang — Baxter 87
Yang — Baxter hexagon 87
Yang — Baxter, YB-operator 87 93
YB-hexagon 87 93
YB-operator under tensor functors 89
YB-operator, balanced 88 89
YB-operator, compatability with duals 89
YB-operator, dualizable 89
YB-operator, given by braiding 89
YB-operator, in braided tensor category 89
YB-operator, left-dualizable 89
YB-operator, tortile 90 91 96
Yetter, David 82
Yoneda Lemma xiv
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте