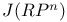|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Husemoller D. — Fibre Bundles |
|
|
 |
| Предметный указатель |
Semiring, ring completion 115 116
Special orthogonal group see “Orthogonal group”
Special unitary group see “Unitary group”
Sphere bundles 253—255
Sphere(s), normal bundle to 13
Sphere(s), tangent bundle of 13 17 98—100 251
Spin group (Spin(n)) 169 170
Spin group (Spin(n)), maximal tori 196 197
Spin group (Spin(n)), real representations of 203—205
Spin group (Spin(n)), representation ring of 200—203
Spin group (Spin(n)), Weyl group of 196 197
Spin representations, complex 198—200 206—208
Spin representations, complex, and 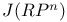 234—239 234—239
Spin representations, complex, real 206—208
Splitting maps 251
Stability of classical groups 94
Stable equivalence (s-equivalence) 111 118—120
Stiefel variety 13 91 92
Stiefel variety, as homogeneous space 87—89
Stiefel variety, homotopy groups of 91—93 95
Stiefel — Whitney classes, axiomatic properties of 247
Stiefel — Whitney classes, definition 247
Stiefel — Whitney classes, definition, by Steenrod squares 257
Stiefel — Whitney classes, dual 278
Stiefel — Whitney classes, multiplicative property of 252 253
Stiefel — Whitney classes, of a manifold 275
Stiefel — Whitney classes, relation of, to orientability 278
Stiefel — Whitney numbers 276
Subbundle 11
Subspace, trivialization over 122
Suspension 5 314
Suspension, decomposition 319—321
Suspension, double 318 333—337
Suspension, fibre bundles over 97
Suspension, sequences 322—323
Symmetric bilinear form 154
Symmetric functions 189—191 285 286
Symplectic group (Sp(n)) 40 87
Symplectic group (Sp(n)) examples 90
Symplectic group (Sp(n)) homotopy groups of 94 104—107
Symplectic group (Sp(n)) infinite 88
Symplectic group (Sp(n)) maximal tori of 193
Symplectic group (Sp(n)) representation ring of 195
Symplectic group (Sp(n)) Weyl group of 193
Tangent bundle, of manifold 263
Tangent bundle, of projective space 14 17 251
Tangent bundle, of sphere 13 17 98—100 251
Thorn isomorphism 258
Thorn space(s) 217—219 258
Thorn space(s), Euler class and 255 258
| Thorn space(s), fibre homotopy type and 227
Topological group 40
Topology, compact-open 4
Torus (tori), maximal see “Maximal tori”
Torus (tori), maximal, representation ring of a 185 186
Total space 11
Transformation group 40
Transition functions 62 63
Trivialization over a subspace 122
Unitary group U(n) and SU(n) 40 87
Unitary group U(n) and SU(n), examples 90
Unitary group U(n) and SU(n), homotopy groups of 94 104—107
Unitary group U(n) and SU(n), infinite 88
Unitary group U(n) and SU(n), maximal tori of 191
Unitary group U(n) and SU(n), representation ring 192
Unitary group U(n) and SU(n), Weyl group of 191
Universal bundle 54 55
Universal bundle, for classical groups 95
Universal bundle, Milnor's construction of 54—56
Universal bundle, Milnor's construction of, verification of universal property 56—58
Universal bundle, of vector bundles 35 96
Vector bundle(s) 24
Vector bundle(s), atlas of charts for 24 62 63
Vector bundle(s), classification 34 35 96
Vector bundle(s), Euler characteristic of stable 136—137
Vector bundle(s), finite type 32
Vector bundle(s), homotopy classification of 28—35 113
Vector bundle(s), induced 27 28
Vector bundle(s), isomorphism of 26
Vector bundle(s), metrics (riemannian and hermitian) 37—38
Vector bundle(s), morphism of 26
Vector bundle(s), orientation of 244 285 286
Vector bundle(s), representations and 177 178
Vector bundle(s), universal bundle of 34 35 97
Vector bundle(s), Whitney sum of 27
Vector fields, and Euler characteristic 274 275
Vector fields, and Euler characteristic, on spheres 24 151 152 168 239
Vector fields, and Euler characteristic, on spheres and  233—235 233—235
Vector fields, and Euler characteristic, on spheres and coreducibility 232—233
Vector fields, and Euler characteristic, reducibility 230—232
Weil, Andre 280
Weyl group, of compact group 184
Weyl group, of compact group, of SO(n) 195 196
Weyl group, of compact group, of Sp(n) 193
Weyl group, of compact group, of Spin(n) 196 197
Weyl group, of compact group, of SU(n) 178 191
Weyl group, of compact group, of U(n) 178 191
Whitney sum of vector bundles 27
Wu's formula 275
Yoneda representation theorem 294 295
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте