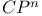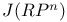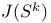|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Husemoller D. — Fibre Bundles |
|
|
 |
| Предметный указатель |
 -ring(s) 171 -ring(s) 171
 -ring(s), -ring(s),  -operations in 175 -operations in 175
 -ring(s), Adams operations in 172 -ring(s), Adams operations in 172
 -ring(s), K(X) and KO(X) as 171 186—188 -ring(s), K(X) and KO(X) as 171 186—188
 -ring(s), representation ring as 180 181 185 -ring(s), representation ring as 180 181 185
 -ring(s), split 174 -ring(s), split 174
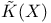 and and 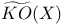 114—117 114—117
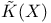 and and 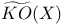 , calculation of , calculation of 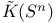 187 188 187 188
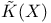 and and 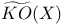 , corepresentation of 118 119 , corepresentation of 118 119
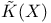 and and 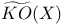 , table of results for , table of results for 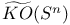 and and 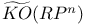 235—237 235—237
Adams conjecture 240
Adams operations 172
Adams operations, in  -rings 172—174 -rings 172—174
Adams operations, on real spin representations 207 238
Alexander duality theorem 271
Atiyah duality theorem 221 222
Atlas of charts, for fibre bundle 62
Atlas of charts, for fibre bundle, for manifold 263
Automorphisms of principal bundles 79—81
Base space 11
Bianchi identity 287
Bilinear form, symmetric 154
Bott periodicity 140 149
Bott periodicity, and integrality theorem 150 236 307 308
Bundle(s) 11
Bundle(s), collapsed 122
Bundle(s), fibre product of 16
Bundle(s), G- 42
Bundle(s), Hopf 141
Bundle(s), induced 18
Bundle(s), locally isomorphic 20
Bundle(s), locally trivial 20
Bundle(s), morphism of 14
Bundle(s), product of 15
Bundle(s), restricted 17
Bundle(s), sub- 11
Bundle(s), sub-, tangent see “Tangent bundle”
Character ring 180
Character ring, representation ring as 180 181
Characteristic classes 295 296 300 304
Characteristic classes and representations 309—311
Characteristic classes, calculations, on canonical line bundles 248 249 259—261
Characteristic classes, calculations, on canonical line bundles, on tangent bundles of 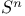 , , 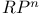 , and , and 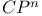 250 251 306 307 250 251 306 307
Characteristic classes, complex 297—299
Characteristic classes, complex, in dimension n 296 298
Characteristic classes, real, mod 2 300—301
Characteristic classes, real, mod 2, 2-divisible 301—304
Characteristic map 101—104
Charts, of fibre bundles 62
Charts, of fibre bundles, of manifolds 263
Charts, of fibre bundles, of vector bundles 24 62
Chern classes 249 296—299
Chern classes, axiomatic properties of 249
Chern classes, definition 249
Chern classes, multiplicative property of 252
Chern forms 286
Chern forms, curvature 284 285
Chern forms, definition 284
Chern forms, homotopy formula 288—291
Chern — Simons invariants 290 291
Classical groups 87—90
Classical groups, classifying spaces for 95 96
Classical groups, examples 89 90
Classical groups, homotopy groups of 95 104—107
Classical groups, infinite 88
Classical groups, stability of 94 95
Classical groups, universal bundle for 95 96
Classifying spaces 63
Classifying spaces, cohomology of 297 300 302
Classifying spaces, for classical groups 95 96
Classifying spaces, of reduced structure group 77
Classifying spaces, of vector bundles 31 32 96
Clifford algebras 156—161
Clifford algebras, calculations of 158
Clifford algebras, table 161
Clifford modules 161—163
Clifford modules, table 163
Clifford modules, tensor products of 166—168
Clutching construction 134—136
Clutching maps 135
Clutching maps, Laurent 142
Clutching maps, linear 145—148
Clutching maps, polynomial 143—145
Cobordism 276—278
coH-space 7
Cokernel of morphism 35—37
Collapsed bundle 122
Compact group 179
Compact group, maximal tori of 182—184
Compact group, rank of 183
Compact group, representation ring of 179—181
Compact group, Weyl group of 184
Compact-open topology 4
Cone over a space 5
Connections on a vector bundle
Coreducible spaces 228
Coreducible spaces, relation to vector fields 179—181
Covariant derivative 292
Cross section(s) 12
Cross section(s), and Euler class 257
Cross section(s), of fibre bundles 48
Cross section(s), prolongation of 21
CW-complex(es) 2
CW-complex(es), homotopy classification over 58
De Rham cohomology 281
Difference isomorphism 131—133
Differential forms 280—283
Duality theorem, Poincare 271
Duality, in manifolds 269—272
Eilenberg — MacLane spaces 83—86
Euclidean inner product 12
Euclidean norm 12
Euclidean space, orientation in 266—267
Euler characteristic, definition 274—275
Euler characteristic, definition, and Euler class 274—275
Euler characteristic, definition, and vector fields 275
Euler characteristic, definition, of stable vector bundles 137
Euler class 254 301—303
Euler class, and cross sections 257
Euler class, and Euler characteristic 274 275
Euler class, and Thorn isomorphism 258
Euler class, definition 254
Euler class, multiplicative property 256 257
Euler class, of a manifold 274 275
Fibre 11
Fibre bundle(s) 45
Fibre bundle(s), atlas of charts for 62
Fibre bundle(s), automorphisms 61 79—81
Fibre bundle(s), classification of 56—59
Fibre bundle(s), cross section of 48
Fibre bundle(s), locally trivial 47
Fibre bundle(s), morphism of 46
Fibre bundle(s), over suspension 85
Fibre bundle(s), trivial 47
Fibre homotopy equivalence 223 224 312 313
Fibre homotopy type 223 224 312 317
Fibre homotopy type and Thorn spaces 227 228
Fibre homotopy type, stable 223—228
Fibre maps 7 312—313
Fibre product 16
Fibre, of a fibre bundle 45
Fibre, of a principal bundle 43
G-module 176
G-module, direct sum of 176
G-module, exterior product of 176
G-module, morphism of 176
G-module, semisimple 177 179
G-module, tensor product of 176
G-space 40
G-space, morphism of 41
| G-space, principal 42
Gauge group, calculation of 81
Gauge group, classifying space of 83
Gauge group, definiton 79—81
Gauge group, universal bundle of 83
Gauss map 33
Grassman manifold (or variety) 13 25 34
Grassman manifold (or variety), as homogeneous space 90 91
Grassman manifold (or variety), cohomology of 297 300 302
Group(s), linear 40
Group(s), reduction of structure 77
Group(s), topological 40
Group(s), transformation 40
Gysin sequence 255
H-space 6
Half-exact cofunctor 138
Half-exact cofunctor, Puppe sequence of 139
Hermitian metrics of vector bundle 37
Homotopy classification, over CW-complexes 58
Homotopy classification, over CW-complexes, of principal bundles 56—58
Homotopy classification, over CW-complexes, of vector bundle 33—35 113 114
Homotopy equivalence 1
Homotopy equivalence, fibre 223 224 285 312 313
Homotopy formula for connections 288—291
Homotopy formula for differential forms 283
Homotopy groups 7
Homotopy groups, of classical groups 94 104—107
Homotopy groups, of O(n) 94 104—107
Homotopy groups, of SO(n) 94 104—107
Homotopy groups, of Sp(n) 94 104—107
Homotopy groups, of Stiefel variety 95 103 104
Homotopy groups, of SU(n) 94 104—107
Homotopy groups, of U(n) 94 104—107
Hopf bundle 142 143
Hopf invariant 210—216 309 326—328
Integrality theorem of Bott 307 308
J(X) 224
J(X), calculation of 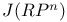 237—239 237—239
J(X), calculation of 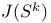 225—227 225—227
K(X) and KO(X) 114—117 120
K(X) and KO(X), and representation ring 180—181
K(X) and KO(X), as  -ring 171 186—188 -ring 171 186—188
K(X) and KO(X), as a ring 128
K(X) and KO(X), Bott periodicity of 140 148—150 236
K-cup product 128
k-space 2
Kunneth formula 85 86
Leray — Hirsch theorem 245
Levi — Civita, connection 291—293
Linear groups 40
Loop space 5
Manifold(s) 262—279
Manifold(s), atlas of charts for 262 263
Manifold(s), duality in 269—272
Manifold(s), Euler class of 274
Manifold(s), fundamental class of 268
Manifold(s), Grassman see “Grassman manifold (or variety)”
Manifold(s), orientation of 267—269
Manifold(s), Stiefel — Whitney classes of 275 276
Manifold(s), tangent bundle to 264
Manifold(s), Thorn class of 272—274
Map space 4
Map(s), fibre 7 312 313
Map(s), Gauss 33
Map(s), normal bundle of 265
Map(s), splitting 251
Mapping cone 125
Mapping cylinder 125
Maximal tori, of compact groups 182—184
Maximal tori, of compact groups, of SO(n) 195 196
Maximal tori, of compact groups, of Sp(n) 193
Maximal tori, of compact groups, of Spin(n) 196 197
Maximal tori, of compact groups, of SU(n) 191
Maximal tori, of compact groups, of U(n) 191
Mayer — Vietoris sequence 246 268—270
Milnor's construction of a universal bundle 54—56
Milnor's construction of a universal bundle, verification of universal property 56—58
Morphism, B- 14
Morphism, cokernel of 36
Morphism, image of 36
Morphism, kernel of 36
Morphism, local representation of 66
Morphism, of bundles 14
Morphism, of fibre bundles 45
Morphism, of G-module 176
Morphism, of G-space 42
Morphism, of principal bundles 43
Morphism, of vector bundles 26
Normal bundle, of an immersion 278
Normal bundle, of an immersion, of a map 265
Normal bundle, of an immersion, to the sphere 13
Numerable covering 49 312
Orientation class 267 268
Orientation, in euclidean space 266 267
Orientation, in euclidean space, of manifolds 267—269
Orientation, in euclidean space, of vector bundles 260
Orthogonal group (O(n)) and (SO(n)) 40 87
Orthogonal group (O(n)) and (SO(n)) examples 90
Orthogonal group (O(n)) and (SO(n)) homotopy groups of 94 104—107
Orthogonal group (O(n)) and (SO(n)) infinite 88
Orthogonal group (O(n)) and (SO(n)) maximal tori of 195 196
Orthogonal group (O(n)) and (SO(n)) representation ring of 200—203
Orthogonal group (O(n)) and (SO(n)) Weyl group of 195 196
Orthogonal multiplication 152 153
Orthogonal splitting 155 156
Path space 5
Poincare duality theorem 271
Pontrjagin classes 259 260 301—304
Principal bundle(s) 42
Principal bundle(s), homotopy classification of 56—58
Principal bundle(s), induced 43
Principal bundle(s), morphism of 42
Principal bundle(s), numerable 49
Products, of bundles 15—17
Products, of bundles, euclidean inner 13
Products, of bundles, of G-module, exterior 176
Products, of bundles, of G-module, tensor 176
Products, of bundles, reduced 5
Projection 11
Projective space 2
Projective space, tangent bundle of 14 17 251
Puppe sequence 125—127 139 220 221
Quadratic form 154
Rank of a compact group 183
Reduced product 5
Reducible spaces 227
Reducible spaces, relation to vector fields 230—232
Representation ring 177—178 203—205
Representation ring, as  -ring 177 178 186 187 -ring 177 178 186 187
Representation ring, character ring as 180 181
Representation ring, K(X) and KO(X) and 177 178
Representation ring, of a torus 185 186
Representation ring, of compact group 179—181
Representation ring, of SO(n) 200—203
Representation ring, of Sp(n) 195
Representation ring, of Spin(w) 200—203
Representation ring, of SU(n) 192
Representation ring, of U(n) 192
Representation ring, real 203—206
Representation ring, real-Spin 203—205
Representation(s) 176—178
Representation(s), and characteristic classes 309—311
Representation(s), and vector bundles 177—178
Representation(s), local, of morphism 66
Representation(s), real, of Spin(w) 203—205
Representation(s), semisimple 179 180
Riemann connection 291—293
Riemannian metrics of vector bundle 37 38
S-category 219—220
Schur's lemma 179
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -ring(s)
-ring(s)  -operations in
-operations in 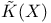 and
and 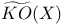
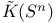
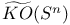 and
and 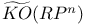
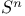 ,
, 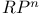 , and
, and