Авторизация
Поиск по указателям
Petersen P. — Riemannian Geometry
Обсудите книгу на научном форуме Нашли опечатку?
Название: Riemannian GeometryАвтор: Petersen P. Аннотация: Intended for a one year course, this volume serves as a single source, introducing students to the important techniques and theorems, while also containing enough background on advanced topics to appeal to those students wishing to specialize in Riemannian geometry. This is one of the few works to combine both the geometric parts of Riemannian geometry and the analytic aspects of the theory, while also presenting the most up-to-date research. This book will appeal to readers with a knowledge of standard manifold theory, including such topics as tensors and Stokes theorem. Various exercises are scattered throughout the text, helping motivate readers to deepen their understanding of the subject.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2nd editionГод издания: 2006Количество страниц: 404Добавлена в каталог: 22.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Angle comparison in negative curvature 167 Arzela — Ascoli lemma 299 Axis for an isometry 167 Berger spheres 7 99 108 179 296 Berger spheres, computation of curvatures 81 Betti number estimate by Bochner 208 Betti number estimate by Gallot — Meyer 212 Betti number estimate by Gromov 358 Betti number estimate by Gromov — Gallot 275 Bianchi's first identity 33 Bianchi's second identity 33 Bochner formula 331 Bochner formula for forms 218 Bochner formula for the curvature tensor 221 Bochner technique for 1-forms 205 Bochner technique for Killing fields 190 Bochner technique in general 209 Bonnet's diameter estimate 170 Bundles of frames 151 Bundles over 2-sphere 18 91 357 373 Busemann function 285 Cartan formalism 59 Cartan's theorem 164 Center of mass 164 Cheeger's lemma 319 Cheng's maximal diameter theorem 270 Christoffel symbols 31 Clifford multiplication 213 Codazzi equation see also Normal curvature equation Cohomology, Cech 383 Cohomology, de Rham 202 384 Cohomology, de Rham, compactly supported 388 Cohomology, Hodge 205 Compact embedding 302 Comparison estimates for Ricci curvature 265 Comparison estimates for sectional curvature 173 Completeness 138 Completeness of closed manifolds 125 Completeness of Gromov— Hausdorff topology 296 Completeness, geodesic 118 Completeness, metric 123 Conjugate point 50 140 176 Conjugate radius estimate 176 Connectedness Lemma for functions 180 Connectedness Lemma for the energy functional 180 Connectedness Principle 181 Connectedness Principle with symmetries 199 Connection along curves 153 Connection form 59 103 Connection of bi-invariant metric see also Metric bi-invariant Connection on Euclidean space 23 Connection on Lie group 56 Connection on vector bundle 209 Connection, affne 26 Connection, representation in a frame 58 Connection, Riemannian 26 Constant curvature 36 Constant curvature, global classiffication 146 Constant curvature, local characterization 135 Contractions 53 Convergence of maps, Gromov — Hausdorff 298 Convergence of pointed spaces, Gromov — Hausdorff 298 Convergence of spaces, Gromov — Hausdorff 294 Convergence of spaces, Hausdorff 294 Convergence of spaces, in Hoelder topology 309 Convergence theorem of Anderson 326 Convergence theorem of Cheeger — Gromov 318 Convexity radius 177 Coordinates, Cartesian, in Euclidean space 23 Coordinates, Cartesian, on Riemannian manifold 133 Coordinates, distance 147 318 Coordinates, exponential 132 Coordinates, harmonic 304 Coordinates, normal at a point 56 Coordinates, polar, in the plane 10 Coordinates, representation of metric in 9 Covariant derivative 27 Covariant derivative in parallel frame 158 Covering space see also Riemannian Critical point estimate 350 Critical point theory 333 Curvature form 59 103 Curvature in dimension 3 38 60 Curvature of a tensor 35 Curvature of product metric see also Product Curvature of tensors 224 Curvature, constant see also Constant curvature Curvature, directional 36 44 Curvature, Gauss 101 Curvature, Isotropic 61 330 Curvature, operator 36 61 212 221 226 358 Curvature, operator, classiffication of 260 Curvature, operator, on symmetric spaces 255 Curvature, representation in a frame 58 Curvature, Ricci 38 265 324 Curvature, Ricci, in harmonic coordinates 305 Curvature, Riemannian 33 Curvature, scalar 39 213 Curvature, sectional 36 61 153 225 333 Cut locus 142 de Rham's decomposition theorem 253 de Rham's theorem 386 Degree of a map 389 Dirac operator 213 Dirac operator on forms 215 Directional derivative 22 Dirichlet problem 304 Displacement function 168 Distance function 41 47 125 133 135 Divergence 28 57 Doubly warped products see also Products Eguchi — Hanson metric 91 Einstein constant 38 Einstein metric 38 254 Einstein notation 8 Einstein tensor 61 Elliptic estimates 303 Elliptic operators 303 Energy functional 126 Euclidean space 2 Euclidean space, curvature of 35 Euler characteristic 102 Exponential map 131 Extrinsic geometry 44 95 Fibration 151 Finiteness theorem for diffeomorphism types 315 320 Finiteness theorem for diffeomorphism types, in positive curvature 319 Finiteness theorem for fundamental groups 277 Finiteness theorem for homotopy types 365 Focal point 50 Frame bundle 190 Frame, left invariant 10 Frame, normal at a point 27 56 Frame, representation of metric in 10 Framing see also Frame Frankel's theorem 182 185 Functional distance see also Metric Fundamental equations for curvature 41 Fundamental equations of Riemannian geometry 47 Fundamental theorem of convergence theory 311 Fundamental theorem of hypersurface theory 100 Fundamental theorem of Riemannian geometry 25 Gauss equation see also Tangential curvature equation Gauss lemma 133 Gauss map 95 Gauss — Bonnet theorem 101 Geodesic 116 131 133 Gradient 22 Grassmannian, compact, as a symmetric space 244 Grassmannian, compact, computation of curvatures 246 Grassmannian, hyperbolic, as a symmetric space 246 Grassmannian, hyperbolic, computation of curvatures 248 Hadamard theorem 96 Hadamard — Cartan theorem 162 Harmonic function 281 hessian 28 Hessian comparison 342 Hinge 338 Hodge star operator 203 Hodge theorem 205 Hoelder norms 301 Holonomy 252 Holonomy classiffication 258 Holonomy of symmetric spaces 258 Homogeneous space 5 Homogeneous space, completeness of 149 Homogeneous space, k-point 184 Hopf fibration 4 6 15 Hopf problem 108 193 212 358 Hopf theorem 102 Hopf — Rinow theorem 137 Hyperbolic space 74 Hyperbolic space as left-invariant metric 80 Hyperbolic space as rotationally symmetric surface 12 Hyperbolic space, geodesics in 120 Hyperbolic space, isometry group of 76 Hyperbolic space, Minkowski space model 75 Hyperbolic space, Riemann's model 74 Hyperbolic space, Rotationally symmetric model 74 Hyperbolic space, upper half plane model 74 Hypersurface in Euclidean space 42 95 Index form 185 Index Lemma 186 Index notation 54 Injectivity radius 142 Injectivity radius estimate by Cheeger 319 Injectivity radius estimate in general 178 Injectivity radius estimate in positive curvature 178 Injectivity radius estimate, generalization of Cheeger's lemma 332 Intrinsic geometry 44 95 101 Isometric immersion see also Riemannian Isometry group 5 189 Isometry group of Euclidean space 5 Isometry group of Hyperbolic space 76 Isometry group of the sphere 5 Isometry, distance-preserving 147 Isometry, Riemannian see also Riemannian Isotropy group 5 Jacobi field along a geodesic 160 Jacobi field for a distance function 48 Killing field 23 188 242 Koszul formula 25 Kuratowski embedding 297 Laplacian connection 209 Laplacian coordiante representation 57 Laplacian estimate 284 Laplacian in harmonic coordinates 305 Laplacian on forms 204 Laplacian on functions 28 Law of Cosines 340 Left invariant frame 10 Left invariant metric see also Metric Length comparison 184 185 Length functional 126 Length of curve in metric space 150 Length of curve in Riemannian manifold 121 Lichnerowicz formula 213 Lie group 6 Lie group, bi-invariant metric see also Metric Lie group, geodesics of bi-invariant metric 151 Lie group, geodesics on 121 Line 282 Local models 331 Maximum principle 58 279 Mayer — Vietoris sequence for de Rham cohomology 384 Metric as a symmetric space 236 250 Metric ball 123 Metric distance 121 Metric on frame bundle 151 Metric on tangent bundle 151 Metric, bi-invariant 18 121 151 291 Metric, computation of curvatures 68 Metric, Einstein 38 Metric, functional 126 151 Metric, homogeneous see also Homogeneous space Metric, Kaehler 62 232 262 263 Metric, left-invariant 6 Metric, local representation of 9 Metric, rotationally symmetric 12 Metric, scalar flat 69 Mixed curvature equation see also normal curvature equation Musical isomorphisms 213 Myers' diameter estimate 171 Norm estimate, using distance functions 318 321 Norm estimate, using exponential maps 318 Norm estimate, using harmonic coordinates 324 Norm of tensors 54 Norm, 302 Norm, 308 Norm, harmonic, for manifolds 321 Norm, weak, for manifolds 332 Norm, weighted, for manifolds 331 Normal curvature equation 45 Normal curvature equation in Euclidean space 97 Obstructions for constant sectional curvature 147 Obstructions for negative curvature operator 108 Obstructions for negative sectional curvature 162 Obstructions for nonnegative sectional curvature 357 Obstructions for positive curvature operator 108 212 Obstructions for positive Ricci curvature 213 Obstructions for positive scalar curvature 213 Obstructions for positive sectional curvature 173 Obstructions for Ricci flatness 288 Parallel curvature 238 Parallel field along curve 156 Parallel field for a distance function 50 Parallel on manifold 28 Parallel vector field 60 Partial derivatives, first 112 Partial derivatives, second 112 Partial derivatives, third 154 partials see also Partial derivatives Partials derivatives and curvature 156 Pinching theorem for Ricci curvature 328 Pinching theorem for sectional curvature 329 Poincare duality 387 Poincare lemma for de Rham cohomology 385 Precompactness theorem for lower Ricci curvature bounds 300 Precompactness theorem for spaces with bounded norm 312 Precompactness theorem in Gromov — Hausdorff topology 299 Preissmann's Theorem 167 Product spheres, computations of curvatures 65 Product, cartesian 17 60 Product, doubly warped 13 Product, doubly warped, computation of curvatures 71 Product, warped 64 Projective space, complex 6 17 97 Projective space, complex, as a symmetric space 248 Projective space, complex, computation of curvatures 85 249 Projective space, complex, holonomy of 263 Projective space, quaternionic 263 Projective space, real 7 Pseudo-Riemannian manifold 4 Quarter pinching 61 346 Radial curvature equation 44 Rank 237 260 Rank of a Lie group 195 Rank, rigidity in nonpositive curvature 260 Ray 282 Riemannian covering 7 144 162
Реклама
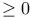
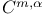, for functions 
|
|
О проекте