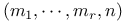јвторизаци€
ѕоиск по указател€м
Hirschfield J.W. Ч Projective Geometries over Finite Fields
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Projective Geometries over Finite Fieldsјвтор: Hirschfield J.W. јннотаци€: This book is an account of the combinatorics of projective spaces over a finite field, with special emphasis on one and two dimensions. With its successor volumes, Finite projective spaces over three dimensions (1985), which is devoted to three dimensions, and General Galois geometries
язык: –убрика: ћатематика /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 1980 оличество страниц: 488ƒобавлена в каталог: 22.05.2008ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
(k,l)-set 70Ч71 (k,l)-span 70 (k,l; r, s; n, q)-set 70 (k,r; n,q)-set 70 (k; r,s; n, q)-set 70 (k;n)-arc 320Ч364 (k;n)-arc of type 321 (k;n)-arc of type m 321Ч322 (k;n)-arc, complete 373 (k;n)-arc, deficiency of a 345Ч355 (k;n)-arc, i-secant of a 320Ч321 (k;n)-arc, maximal 324Ч335 (k;n)-arc, of type (0, 1, n) 342Ч343 (k;n)-arc, of type (m,n) 335Ч345 (k;n)-arc, t-maximal 335 338Ч341 (k;n)-arc, t-minimal 338Ч341 (k;r)-arc 70 (k;r)-cap 70 a-arc 186Ч199 235 Absolutely irreducible primal 50 Absolutely irreducible primal, variety 51 Acnode 223 Affine space 37 332Ч335 Affine space, axioms for 38Ч40 Arc, Herraitian 329 337Ч341 343Ч345 Arc, maximal 324Ч335 Associated point 128 132Ч133 Automorphism of a field 1 4 Automorphism of a space 30 Axioms for affine space 38Ч40 Axioms for projective space 38Ч39 B-point 393Ч395 397Ч404 408Ч414 Base point 55 Basis for a coordinate system 32 Bezout's theorem 223 Bisecant 70 Bisecant of a k-arc 165 Block 57 Blocking set 366Ч385 Blocking set, k-arc derived 366Ч367 Blocking set, minimal 366Ч368 373 Brianchon hexagon 393 Brianchon hexagon, point 393Ч395 397Ч404 408Ч414 Camot's theorem 57Ч58 Canonical form for a Hermitian variety 98Ч99 Canonical form for a polarity 110Ч115 Canonical form for a projectivity 40Ч46 124Ч128 149Ч157 Canonical form for a quadric 98Ч102 104Ч107 Category of a polyomial 13 19Ч20 Category of an element 4 13 Ceva's theorem 60 Character of a field 19 Characteristic of a field 1 Chord of a k-set 70Ч71 Class of a cubic curve 252 Collineation 30 Collineation, group 40Ч41 244 419Ч424 Committee 366 373 Companion matrix 44 Complete k-arc 163 232Ч239 Complete K-set 70 Complete series 54 Complex conjugate points 50 Complex inflexion 249 271 Complex point 50 Component of a curve 221 Component of a curve, irregular 221 Component of a curve, linear 221 Component of a curve, regular 221 Component of a primal 50 Component of a variety 51 Cone 51 Configuration, collineation group of a 244 Configuration, permutation group of a 244 Configuration, projective group of a 244 conic 107 140Ч146 235Ч239 Conic, nucleus of a 143 Conic, projective group of a 143Ч144 156Ч157 Conjugacy classes in GL(2,q) 124Ч125 Conjugacy classes in GL(3,q) 149Ч152 Conjugacy classes in PGL(2tq) 124Ч128 Conjugacy classes in PGL(5,q) 149Ч157 Conjugacy classes, number of 42 61Ч62 Conjugate points 33 Conjugate points, primes 33 Coordinate of a line 166 Coordinate system 31Ч32 Coordinate, non-homogeneous 54 119 Coordinates, prime 32Ч33 Coordinates, tangential 32Ч33 Correlation 33 Cross-axis of a projectivity 161 Cross-ratio 22Ч23 119Ч120 Crunode 223 Cubic curve with an isolated double point 226 259Ч268 Cubic curve with nine inflexions 278Ч280 Cubic curve with no inflexions 308Ч311 Cubic curve with one inflexion 282Ч307 Cubic curve with three inflexions 280Ч282 Cubic curve, equations 13 16 18Ч22 Cubic curves 225Ч226 241Ч318 357Ч358 361Ч363 Cubic curves equianharmonic 253 277 Cubic curves general 254 277 Cubic curves harmonic 253 277 Cubic curves nodal 226 254Ч256 267Ч268 Cubic curves non-singular 270Ч318 Cubic curves nucleus of 241 Cubic curves number of points on 311Ч313 Cubic curves singular 254Ч268 Cubic curves superharmonic 253 Cubic curves, classification of non-singular 313Ч318 Cubic curves, classification of singular 266Ч268 Cubic curves, cuspidal 226 256Ч259 267Ч268 Curve 49 51 Curve, genus of a 226Ч227 Curve, Hermitian 146Ч148 227 243 Curve, sub-Hermitian 148Ч149 227 Curves, cubic 225Ч226 241Ч318 361Ч363 Cusp 223 Cyclic projectivity 74Ч96 155 d-secant 70 Degree of a primal 49 Degree of of a variety 51 Desargues's theox-em 160Ч161 Design 37 Diagonal points of a pentastigm 139Ч140 Diagonal points of a tetrastigm 138 Diagonal points of an n-stigm 139Ч140 Dickson's criterion 3 Dimension of a projective space 29 Dimension of a variety 51 Dimension of a vector space 29 Dimension of an affine space 37 Discriminant 3 10 Dual space 31 Duality, principle of 31 Elation 153 Elementary divisor 43Ч46 Elementary divisor, operation 43 Elliptic quadric 106Ч111 114Ч115 Equations, cubic 13 16 18Ч22 Equations, equianharmonic quartic 22 25Ч27 Equations, harmonic quartic 22 Equations, quadratic 3 13 Equations, quartic 13 16Ч18 22Ч27 Equianharmonic quartic equations 22 25Ч27 Equianharmonic tetrad 121Ч122 130Ч131 Equivalence of matrices 43 EXPONENT 6 Extended symbol of a linear transformation 45Ч46 Extended symbol of a projectivity 45Ч46 External line of a k-arc 163 External line of an oval (conic) 165Ч166 170Ч171 External line, point of a k-arc 201 Field 1 finite 1 Finite fields 1Ч27 Finite fields, addition tables for 425Ч429 First polar 245Ч246 FORM 49 Fundamental theorem of projective geometry 30Ч31 General linear group 41 419Ч424 Generalized quadrangle 37 Grade of a point 164 Group, collineation 40Ч41 244 419Ч424 Group, general linear 41 124Ч125 149Ч152 419Ч424 Group, isomorphisms 422Ч424 Group, order of a semi-linear 420Ч421 Group, permutation 244 Group, projective 40 124Ч128 149Ч157 244 419Ч424 Group, projective, orthogonal 110 143Ч144 156Ч157 419Ч424 Group, projective, pseudo symplectic 113 174 419Ч424 Group, projective, special linear 41 419Ч424 Group, projective, symplectic 113 419Ч424 Group, projective, unitary 110 147 419Ч424 Group, special linear 41 419Ч424 Harmonic 152 Harmonic homology 152 Harmonic homology, polar 248 Harmonic homology, quartic equation 22 Harmonic homology, separation 120 Harmonic homology, syntheme 129Ч130 Harmonic homology, tetrad 120Ч121 129Ч131 133Ч135 169Ч170 Harmonic homology, tetrad, negative 134Ч135 Harmonic homology, tetrad, positive 134Ч135 Hasse Ч Weil theorem 225Ч232 Hermitian arc 329 337Ч341 343Ч345 Hermitian curve 146Ч148 228Ч229 243 Hermitian polarity 35Ч36 110 147Ч148 Hermitian variety 97Ч100 102Ч103 110Ч111 115 Hermitian variety in the plane 146Ч148 Hermitian variety on a line 122Ч123 Hermitian variety, canonical form for a 98Ч99 Hermitian variety, degenerate 97 Hermitian variety, group of a 110 Hermitian variety, number of points on a 102Ч103 Hessian of a cubic curve 246 Hessian polynomial 18Ч22 Hessian, indeterminate 248 Hexagon 55 Hexagon, Brianchon 393 Hexagon, Pascal 394 Hexastigm 55 Hexastigms, number of, not on a conic 142Ч143 Homology 152 Hyperbolic quadric 106Ч111 114Ч115 Hypercompanion matrix 44 Hyperplane 29 Hypersurface 49 Ideal line 38 74 Ideal point 38 74 Imaginary point 50 Incidence of subspaces 29 Incidence structure 37Ч40 74 Index of a k-arc 201 205Ч206 Index of a point 164 Inflexion 222 Inflexion of a cubic 246Ч250 Inflexional line 277 Inflexional tangent 246 Inflexional triangle 271 277 Internal point of a conic 165Ч166 170Ч171 Internal point of a k-arc 201 Intersection cycle 253 Intersection multiplicity 52 223 Intersection of subspaces 30 Invariant factor 43Ч44 46 Invariant, absolute 278 308 Invariants of polynomials 10Ч27 Involution 126Ч128 Involution, elliptic 126Ч128 Involution, hyperbolic 126Ч128 Involution, improper 126Ч128 Involution, parabolic 126Ч128 Involution, proper 126Ч128 Irreducible primal 50 Irreducible variety 51 Isolated double point 222 Isomorphisms of groups 422Ч424 Join 30 k-arc 54Ч55 70 163Ч219 387Ч414 k-arc, bisecant of a 163 k-arc, complete 163 205Ч208 214Ч219 232Ч239 k-arc, external line of a 163 k-arc, external line of a, point of a 201 k-arc, grade of a point off a 164 k-arc, index of a 201 205Ч206 k-arc, index of a, of a point off a 164 k-arc, internal point of a 201 k-arc, rank of a 201 205Ч206 k-arc, rank of a, of a point off a 204 k-arc, symmetric 207 k-arc, uniform 212Ч214 k-arc, unisecant of a 163 166Ч168 k-arcs, number of 137 k-cap 70 k-fold spread 81 k-set 69Ч71 k-set, chord of a 70Ч71 k-set, complete 70 k-set, tangent to a 70 Lagrange's interpolation formula 2 Line 29 38 119Ч135 Line, Hermitian variety on a 122Ч123 Line, ideal 38 74 Line, inflexional 277 Line, polarity on a 123 Line, projectivity on a 119 124Ч128 Line, proper 74 Line, quadric on a 122 Line, tangent 52 Linear independence 29 Linear series 54 Linear subsystem 53 Linear system 53Ч60 Linear transformation, extended symbol of a 45Ч46 Linear transformation, order of a 48Ч49 Linear transformation, symbol of a 45Ч46 Lines, parallel 38 332Ч335 Meet of subspaces 30 Menelaus's theorem 57Ч58 Model point 225 Multiplicity of a point 52 222 n-arc 54Ч55 n-curve 359Ч364 n-curve, complete 360 n-curve, multiple point on an 359Ч361 n-curve, multiplicity of a point on an 359 n-curve, simple point on an 359 N-gram 54Ч55 n-point 54Ч55 n-side 54Ч55 n-stigm 54Ч55 n-stigms, number of 137 Net 53 Node 222 Non-Desarguesian plane 74 Non-homogeneous coordinate 54 119 Nucleus of a (q+1)-arc 164Ч165 Nucleus of a conic 143
–еклама
 |
|
ќ проекте
|
|
ќ проекте