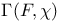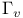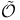|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rumely R.S. — Capacity Theory on Algebraic Curves |
|
|
 |
| Предметный указатель |
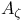 --capacitability 259 --capacitability 259
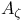 --capacitability, pathological examples 264—266 --capacitability, pathological examples 264—266
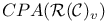 113 115 113 115
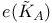 322 336 322 336
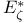 140 146 195 140 146 195
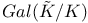 , action on probability vectors 321 , action on probability vectors 321
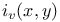 for curves of arbitrary genus 96 107 for curves of arbitrary genus 96 107
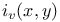 for Tate curves 94—96 for Tate curves 94—96
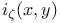 96 107 96 107
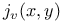 for curves of any genus 116 for curves of any genus 116
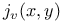 for Tate curves 94—96 for Tate curves 94—96
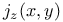 , , 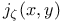 107 109 110 222 107 109 110 222
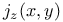 , , 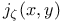 , continuity of 112 , continuity of 112
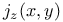 , , 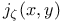 , extension to , extension to 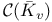 120 120
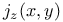 , , 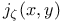 , mean value property for 108 , mean value property for 108
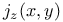 , , 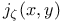 , polarization identity for 112 , polarization identity for 112
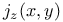 , , 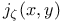 , satisfies Laplace equation 109 , satisfies Laplace equation 109
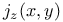 , , 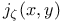 , takes rational values at rational points of , takes rational values at rational points of 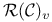 112 112
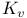 -symmetric set -symmetric set 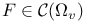 311 321 311 321
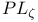 -domain, definition 50 236 -domain, definition 50 236
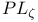 -domain, finite unions of isometrically parametrizable balls 252 -domain, finite unions of isometrically parametrizable balls 252
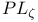 -domain, independent of -domain, independent of  244 252 244 252
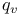 20 20
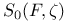 292 293 292 293
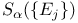 , , 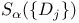 285 285
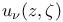 135 135
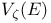 (“Robbin’s constant”), bound for unions of sets 148 198 (“Robbin’s constant”), bound for unions of sets 148 198
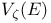 (“Robbin’s constant”), definition 136 190 (“Robbin’s constant”), definition 136 190
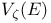 (“Robbin’s constant”), extremal properties 136 147 197 (“Robbin’s constant”), extremal properties 136 147 197
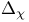 (“sum of slopes” operator) 113 256 (“sum of slopes” operator) 113 256
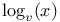 20 185 20 185
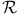 -disc 222 -disc 222
 -capacitable set 327 414 -capacitable set 327 414
 -trivial set 323 -trivial set 323
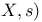 -function 383 -function 383
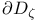 . (“outer boundary”) 143 146 . (“outer boundary”) 143 146
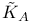 336 336
A-disc, A-codisc 224
A.C. sets are approximatable by PL-domains, RL-domains 311—316
A.C. sets are closed 276
Abel map 48
Abelian integral 64
Abhyankar, S. 97
Absolute values (conventions) 20
Adelic neighborhood 322 336
Adelic set 322 336
Ahlfors, L. 160 162
Algebraic capacitability 15 258
Algebraic capacitability, Choquet’s theorem fails 265
Algebraic capacitability, compact sets are A.C. 262
Algebraic capacitability, finite unions of open balls, closed balls are A.C. 274
Algebraic capacitability, finite unions, intersections of RL-domains, compact sets are A.C. 266
Algebraic capacitability, non-A.C. sets 263—264
Algebraic capacitability, not stable under intersections 266
Algebraic capacitability, PL-domains are A.C. 258
Algebraic capacitability, pullbacks of A.C. sets are A.C. 274 304—309
Algebraic capacitability, RL-domains are A.C. 260
Algebraic curves (conventions) 21
Algebraic integers 1 9 373 376
Algorithm for finding 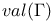 367 367
Algorithm for finding minimal model 101
Analytic arc 162 165 167
Approximation of 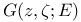 , (Archimedean case), basic theorem 168 , (Archimedean case), basic theorem 168
Approximation of 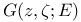 , (Archimedean case), independent variability of leading coeffs 173—184 , (Archimedean case), independent variability of leading coeffs 173—184
Approximation of 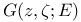 , (Archimedean case), input to Fekete — Szego theorem 171 173 , (Archimedean case), input to Fekete — Szego theorem 171 173
Approximation of 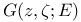 , (Nonarchimedean case), input to Fekete — Szego theorem 318 319 , (Nonarchimedean case), input to Fekete — Szego theorem 318 319
Arakelov function 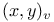 13 14 80 89 13 14 80 89
Arakelov function 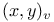 , (Archimedean case) for , (Archimedean case) for 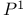 80 80
Arakelov function 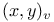 , (Archimedean case) for curves of genus , (Archimedean case) for curves of genus  83 83
Arakelov function 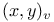 , (Archimedean case) for elliptic curves 82 , (Archimedean case) for elliptic curves 82
Arakelov function 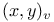 , (Archimedean case), axioms for Arakelov Green’s functions 80 , (Archimedean case), axioms for Arakelov Green’s functions 80
Arakelov function 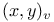 , (Archimedean case), in terms of , (Archimedean case), in terms of ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) 86 86
Arakelov function 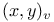 , (Archimedean case), non-normalized 80 , (Archimedean case), non-normalized 80
Arakelov function 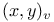 , (Nonarchimedean case) for , (Nonarchimedean case) for 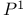 90 90
Arakelov function 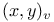 , (Nonarchimedean case) for curves of genus , (Nonarchimedean case) for curves of genus  96 115—116 96 115—116
Arakelov function 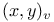 , (Nonarchimedean case) for curves w/good reduction 90 , (Nonarchimedean case) for curves w/good reduction 90
Arakelov function 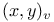 , (Nonarchimedean case) for Tate curves 93 , (Nonarchimedean case) for Tate curves 93
Arakelov function 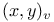 , (Nonarchimedean case), comparability with , (Nonarchimedean case), comparability with 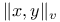 128 128
Arakelov function 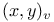 , (Nonarchimedean case), definition 89 , (Nonarchimedean case), definition 89
Artin contraction theorem 19
Artin, M. 97 118
Balancing 397
Ball, boundary of 30
Ball, conventions 22 30 185
Ball, isometrically parametrizable 31 185—186
Ball, parametrizable 30
Ball, rational, irrational 186
Barrier 143
Basis functions 382
Bent line segments 342
Bertrandias, F. 2
Blowing up 101 102 117 118 121
Borel measure 135 186
Boundary of ball or disc 30
Boundary of disc or codisc 239
Boundary of island domain 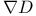 239 239
Boundary of R-disc 239
Boundary of RL-domain 50
Bourbaki, H. 45 321
Brown, S. 30
Bsilinson, A.A. 18
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) 12 14 12 14
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , (Nonarchimedean case) for , (Nonarchimedean case) for 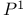 90 90
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , (Nonarchimedean case) for curves w/good reduction 90 , (Nonarchimedean case) for curves w/good reduction 90
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , (Nonarchimedean case) for Tate curves 93 , (Nonarchimedean case) for Tate curves 93
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , (Nonarchimedean case) local ultrametric inequality 130 , (Nonarchimedean case) local ultrametric inequality 130
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , (Nonarchimedean case), weak triangle inequality 127 , (Nonarchimedean case), weak triangle inequality 127
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , approximatable by , approximatable by 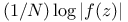 72 72
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , change of centers formula 72 , change of centers formula 72
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , characterization of 69 , characterization of 69
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , construction of 58 63 , construction of 58 63
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , definition 57 , definition 57
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , factorization property 57 , factorization property 57
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , Galois stability 57 61 , Galois stability 57 61
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , Gross’s formula for 13 77 106 , Gross’s formula for 13 77 106
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , in terms of Neron’s pairing 77 106 , in terms of Neron’s pairing 77 106
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , invariance under base change 90 , invariance under base change 90
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , joint continuity in x, y 57 61 63 66 67 69—70 , joint continuity in x, y 57 61 63 66 67 69—70
Canonical distance ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) , weak triangle inequality 73 127 , weak triangle inequality 73 127
Canonical metric 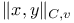 103 221 103 221
Canonical metric 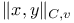 , comparability with , comparability with 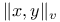 120 120
Canonical metric 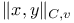 , ultrametric inequality for 104 224 , ultrametric inequality for 104 224
Cantor set 347
Cantor, D. 2 6 10 16 50 220 226 320 328 332 355 369 381
Capacity, (Archimedean case), capacity of 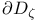 , , 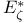 146 146
Capacity, (Archimedean case), definition, 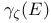 for compact sets 136 for compact sets 136
Capacity, (Archimedean case), definition, 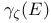 for compact sets, for arbitrary sets 137 for compact sets, for arbitrary sets 137
Capacity, (Archimedean case), equality with 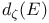 151 151
Capacity, (Archimedean case), examples 338—347
Capacity, (Archimedean case), limits of open sets 149
Capacity, (Archimedean case), sets of capacity 0 133 134 137 137
Capacity, (Archimedean case), table of capacities 348—351
Capacity, (Archimedean case), unchanged by sets of capacity, capacity 0 149
Capacity, (Nonarchimedean case) for countable sets 200
Capacity, (Nonarchimedean case), algorithm for computing capacity of a union of sets 353—355
Capacity, (Nonarchimedean case), countable unions 193
Capacity, (Nonarchimedean case), definition, 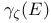 for compact sets 190 for compact sets 190
Capacity, (Nonarchimedean case), definition, 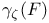 for general sets 259 for general sets 259
Capacity, (Nonarchimedean case), definition, 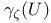 for PL-domains 259 for PL-domains 259
Capacity, (Nonarchimedean case), dependence on ground field 352
Capacity, (Nonarchimedean case), equality with 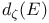 204 204
Capacity, (Nonarchimedean case), examples 211—219 352—365
Capacity, (Nonarchimedean case), examples for Elliptic curves 360—365
Capacity, (Nonarchimedean case), inner capacity 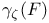 15 192 259 15 192 259
Capacity, (Nonarchimedean case), limits of open sets 200
Capacity, (Nonarchimedean case), outer capacity 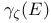 15 259 15 259
Capacity, (Nonarchimedean case), unchanged by capacity 0 sets 199
Capacity, (Nonarchimedean case), unions of compact sets 201
Capacity, , (Global capacity) 3 10 171 163
Capacity, , (Global capacity) for elliptic curves 5 370
| Capacity, , (Global capacity), algorithm for computing 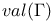 366—367 366—367
Capacity, , (Global capacity), base extension 333
Capacity, , (Global capacity), definition of 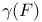 328 328
Capacity, , (Global capacity), monotonicity properties 331—332
Capacity, , (Global capacity), pullbacks 333
Capacity, , (Global capacity), separation inequality on 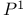 333 333
Carrier 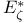 140 146 195 140 146 195
Cauchy estimates 34 35 36
Centers 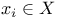 322 322
Chebyshev constants 7 150 203
Chinbnrg, T. 19 79 103
Choqust, G. 265
Chordal distance 23 25 26
Chordal distance as Arakelov Green’s function 81
Circuit model 110
Codisc 22
Conductor potential 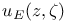 , (Archimedean case), constant on E 143 , (Archimedean case), constant on E 143
Conductor potential 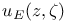 , (Archimedean case), continuity properties 142 , (Archimedean case), continuity properties 142
Conductor potential 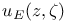 , (Archimedean case), definition 137 , (Archimedean case), definition 137
Conductor potential 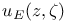 , (Archimedean case), uniqueness 145 , (Archimedean case), uniqueness 145
Conductor potential 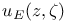 , (Nonarchimsdsan case), constant on E 195 , (Nonarchimsdsan case), constant on E 195
Conductor potential 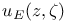 , (Nonarchimsdsan case), definition 191 , (Nonarchimsdsan case), definition 191
Conductor potential 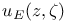 , (Nonarchimsdsan case), examples 211—219 , (Nonarchimsdsan case), examples 211—219
Conductor potential 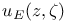 , (Nonarchimsdsan case), examples for finite unions 216 , (Nonarchimsdsan case), examples for finite unions 216
Conductor potential 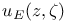 , (Nonarchimsdsan case), examples for pullbacks 214 , (Nonarchimsdsan case), examples for pullbacks 214
Conductor potential 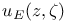 , (Nonarchimsdsan case), examples for rings of integers 212 , (Nonarchimsdsan case), examples for rings of integers 212
Conductor potential 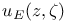 , (Nonarchimsdsan case), less than , (Nonarchimsdsan case), less than 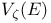 off E 197 off E 197
Conductor potential 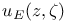 , (Nonarchimsdsan case), pathological examples 217 , (Nonarchimsdsan case), pathological examples 217
Conductor potential 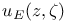 , (Nonarchimsdsan case), uniqueness 211 , (Nonarchimsdsan case), uniqueness 211
Continuum 156
Convex hull 174
Coordinate patches 133
Currents 86
deg(f) 21
Degree sequence 381
Deligne — Mumford Theorem 101 118
Dictionary between circuits, harmonic functions on graphs 110
Differentials of 1st, 3rd kinds 64
Dirichlet — Minkowski Unit Theorem 395
Disc with respect to 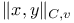 222 222
Disc, boundary of 30
Disc, conventions 22 356
Disc, isometrically parametrizable 30
Disc, open, closed 30
Divisor function 113
Dwork, B. 17 39 40
Electric circuit analogy 110
Electrostatic analogy for capacity 6 8
Elliptic curve 5 361 370
Energy integral 136
Equilibrium distribution 7
Equilibrium distribution, (Archimedean case), definition 137
Equilibrium distribution, (Archimedean case), examples of 163
Equilibrium distribution, (Archimedean case), formula in terms of 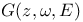 162 162
Equilibrium distribution, (Archimedean case), uniqueness 145
Equilibrium distribution, (Nonarchimedean case), definition 190
Equilibrium distribution, (Nonarchimedean case), examples 211—219
Equilibrium distribution, (Nonarchimedean case), examples for finite unions of sets 216
Equilibrium distribution, (Nonarchimedean case), examples for pullbacks 214
Equilibrium distribution, (Nonarchimedean case), examples for rings of integers 212—213
Equilibrium distribution, (Nonarchimedean case), pathological examples 217
Equilibrium distribution, (Nonarchimedean case), uniqueness 211
Evans function 208
Exponential map 49
Fekete points 152
Fekete — Szego Theorem for algebraic curves 4 414 415
Fekete — Szego Theorem in classical case 1 2 373 376
Fekete — Szego Theorem when 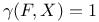 416 416
Fekete — Szego Theorem, archimedean input 171 173
Fekete — Szego Theorem, inner vs outer capacity appropriate for 418—420
Fekete — Szego Theorem, nonarchimedean input 316 318 319
Fekete, M. and Szego.G. 1 2 3 4 6 9 15 373
Fine cover 187
Fine subcover 187
Frobenius’s Theorem 328—329
Frostman’s Theorem 140 195 284
Frssnsl, J. 220
Fubini — Study metric 23 26
Fulton, V. 117
Function suitable for defining ![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif) 59 59
Fundamental group 63
Fundamental Theorem of Game Theory 327 335
Generalized disc 222
Generic value of 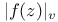 223 223
Generic value of 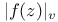 , , 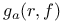 224 224
Generic value of 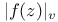 , ,  224 224
Geodesic 26
Gillet, H. 18
Global mapping functions 381
Global mapping functions, when 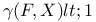 384—393 384—393
Global mapping functions, when 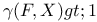 395—413 395—413
Good reduction 91 322 323 383 411
Green’s function  8 10 14 155 277 8 10 14 155 277
Green’s function  , (Archimedean case), approximatable by , (Archimedean case), approximatable by 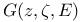 of good sets 165 of good sets 165
Green’s function  , (Archimedean case), approximatable by (1/N)log|f(z)| 168 , (Archimedean case), approximatable by (1/N)log|f(z)| 168
Green’s function  , (Archimedean case), basic properties 156 , (Archimedean case), basic properties 156
Green’s function  , (Archimedean case), behavior under limits 158—159 , (Archimedean case), behavior under limits 158—159
Green’s function  , (Archimedean case), continuity in two variables 161 , (Archimedean case), continuity in two variables 161
Green’s function  , (Archimedean case), definition of 155 , (Archimedean case), definition of 155
Green’s function  , (Archimedean case), functoriality 163 164 , (Archimedean case), functoriality 163 164
Green’s function  , (Archimedean case), monotonicity 157 , (Archimedean case), monotonicity 157
Green’s function  , (Archimedean case), positivity off E 156 , (Archimedean case), positivity off E 156
Green’s function  , (Archimedean case), symmetry 160 , (Archimedean case), symmetry 160
Green’s function  , (Nonarchimedean case), , (Nonarchimedean case), 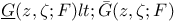 278 282 278 282
Green’s function  , (Nonarchimedean case), , (Nonarchimedean case), 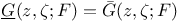 off F, for A.C. sets 283 291 293 off F, for A.C. sets 283 291 293
Green’s function  , (Nonarchimedean case), behavior under pullbacks 305 , (Nonarchimedean case), behavior under pullbacks 305
Green’s function  , (Nonarchimedean case), continuity of , (Nonarchimedean case), continuity of 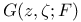 301 301
Green’s function  , (Nonarchimedean case), definition: , (Nonarchimedean case), definition: 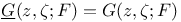 for A.C. sets 297 for A.C. sets 297
Green’s function  , (Nonarchimedean case), dependence on ground field 35 , (Nonarchimedean case), dependence on ground field 35
Green’s function  , (Nonarchimedean case), examples of non-A.C, sets, where upper, lower Green’s functions differ 282—283 , (Nonarchimedean case), examples of non-A.C, sets, where upper, lower Green’s functions differ 282—283
Green’s function  , (Nonarchimedean case), examples with , (Nonarchimedean case), examples with 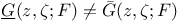 on F 295 on F 295
Green’s function  , (Nonarchimedean case), Galois stability 310 , (Nonarchimedean case), Galois stability 310
Green’s function  , (Nonarchimedean case), lower: , (Nonarchimedean case), lower:  277 282 277 282
Green’s function  , (Nonarchimedean case), monotonicity in F 297 , (Nonarchimedean case), monotonicity in F 297
Green’s function  , (Nonarchimedean case), sequence Green’s functions , (Nonarchimedean case), sequence Green’s functions 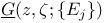 , , 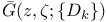 283 283
Green’s function  , (Nonarchimedean case), symmetry of , (Nonarchimedean case), symmetry of 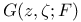 299 299
Green’s function  , (Nonarchimedean case), the zero set , (Nonarchimedean case), the zero set 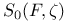 292 292
Green’s function  , (Nonarchimedean case), upper: , (Nonarchimedean case), upper:  277 282 277 282
Green’s function  , (Nonarchimedean case), upper: , (Nonarchimedean case), upper: 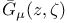 208 208
Green’s function  , (Nonarchimedean case), well defined 278 , (Nonarchimedean case), well defined 278
Green’s identity 67 87 160 161
Green’s matrix, 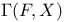 well-defined 327 well-defined 327
Green’s matrix, 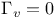 for almost all v 324 for almost all v 324
Green’s matrix, global Green’s matrix 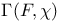 1 325 326 1 325 326
Green’s matrix, Gross, B. 12 19 63 74 77 83 89 106
Green’s matrix, local Green’s matrix 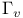 11 324 326 11 324 326
Green’s matrix, reducible vs irreducible 328 369
Grothendieck, A. 99
Gunning, R. 63 64 65
Haar measure 23
Hadamard Quotient Theorem 18
Half-disc 340
Harbatsr, D. 19 27
Harmonic function 63 73
Harnack’s principle 70
Hartogs, F. 65
High order coefficients 374 378 389 408
Hilbert’s 10th problem for 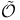 6 6
Hilbert’s Lemniscate Theorem 168
Hills, E. 168 374
Hole (of codisc) 223 225
Horizontal divisor 98
Hriljac, P. 106
Hyperbolic polygon group 83
Independent variability of leading coefficients 173
Inner capacity 192
Inner capacity for a PL-domain 258
Intersection pairing 98
Intersection pairing for divisors of functions 100
Intersection pairing for horizontal divisors 99
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



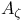 --capacitability
--capacitability 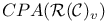
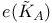
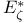
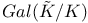 , action on probability vectors
, action on probability vectors 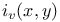 for curves of arbitrary genus
for curves of arbitrary genus 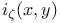
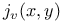 for curves of any genus
for curves of any genus 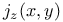 ,
, 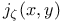
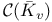
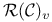
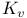 -symmetric set
-symmetric set 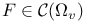
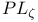 -domain, definition
-domain, definition 
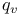
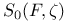
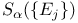 ,
, 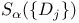
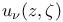
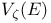 (“Robbin’s constant”), bound for unions of sets
(“Robbin’s constant”), bound for unions of sets 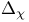 (“sum of slopes” operator)
(“sum of slopes” operator) 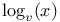
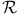 -disc
-disc  -capacitable set
-capacitable set 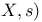 -function
-function 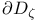 . (“outer boundary”)
. (“outer boundary”) 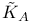
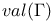
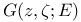 , (Archimedean case), basic theorem
, (Archimedean case), basic theorem 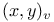
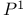

![$[x, y]_{\zeta}$](/math_tex/1b962850b94a00eb6e4c63c6d77b2f7082.gif)
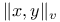
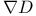
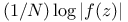
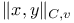
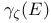 for compact sets
for compact sets 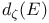
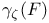 for general sets
for general sets 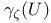 for PL-domains
for PL-domains 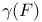
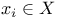
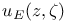 , (Archimedean case), constant on E
, (Archimedean case), constant on E 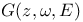
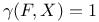
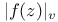
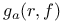

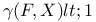
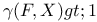

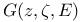 of good sets
of good sets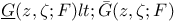
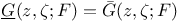 off F, for A.C. sets
off F, for A.C. sets 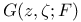
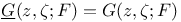 for A.C. sets
for A.C. sets 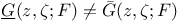 on F
on F 
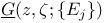 ,
, 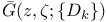

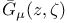
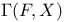 well-defined
well-defined 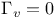 for almost all v
for almost all v