|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Sokolnikoff I.S. — Mathematics of Physics and Modern Engineering |
|
|
 |
| Предметный указатель |
Irrotational flow 412
Isoclines 36
Isolated singular points 569
Iterative methods 679 684 689 721—730
Jacobian 238 212p 271
Jump of a function 520
kinetic energy 43 306p
Kronecker delta 321
Lagrange’s differential equation 26
Lagrange’s interpolation formula 699
Lagrange’s multipliers 250 254
Laplace transform 754—769
Laplace transform of derivatives 756
Laplace transform of Dirac’s “function” 759
Laplace transform, bilateral 762n
Laplace transform, convolution theorem for 762
Laplace transform, Heaviside’s theorem on 766
Laplace transform, solution by, of differential equations 756—762
Laplace transform, solution by, of integral equations 767
Laplace transform, tables of 770
Laplace transform, unilateral 762n
Laplace — de Moivre limit theorem 648
Laplace’s difference equation 511 735
Laplace’s equation 409 413 416 419 464 467 735
Laplace’s law in probability 647
Laplacian operator 387
Laplacian operator in curvilinear coordinates 407
Laurent’s expansion 564
Laurent’s expansion, uniqueness of 567
Laurent’s theorem 565
Law of errors 662
Law of Large Numbers 650
Law of mechanics 302
Law of probability, binomial 639 647
Law of probability, normal 647 653
Law of reflection 297p
Law of refraction 297p
Law of small numbers 654
Law, Newton’s see “Newton’s law”
Law, parallelogram 288 529
Least squares 663p 702
Least squares, connection with orthogonal functions 200
Least squares, curve fitting by 702
Lebesgue integral 774
Lebesgue theorem 775
Legendre polynomials 159
Legendre polynomials, expansion in series of 196 473
Legendre polynomials, generating function for 159p
Legendre polynomials, orthogonality of 198
Legendre polynomials, Rodrigues’ formula for 159p
Legendre’s equation 158
Leibniz’ formula for differentiation of integrals 262
Leibniz’ formula, use in evaluating integrals 263
Leibniz’ test 128
Length of arc 301 362
Length of arc of an ellipse 147
Level surface 369
Line integrals 373
Line integrals in complex plane 545
Line integrals independent of path 378 393
Line integrals of analytic functions 547—554
Line integrals of vector functions 374
Line integrals, transformation of 382—402
Line, equation of 306
Linear algebraic equations 350 687 689 749
Linear dependence 52 70
Linear dependence of vectors 317
Linear differential equations see “Ordinary differential equations”
Linear fractional transformation (bilinear transformation) 577p
Linear operators 336 754
Linear transformation 332
Linear vector spaces 316
Linearity, property of 51
Lipschitz condition 38
Log z 537 581
Logarithmic function 537 581
Logarithmic function, principal value of 537
Lower bound 773
M test 134
MacLaurin’s Formula 260
Maclaurin’s series 144
Mapping, by analytic functions 575—594
Mapping, conformal see “Conformal mapping”
Mass, center of 303
Mass, motion of 44 304
Matrices, algebraic operations on 327—331
Matrices, inversion of 333 350
Matrices, product of 328
Matrices, transformation of 340—350
Matrix 327 749
Matrix identity 329
Matrix, augmented 750
Matrix, characteristic equation of 344
Matrix, characteristic values of 344
Matrix, conjugate 343
Matrix, determinant of 750
Matrix, diagonal 329 339 343
Matrix, hermitian 349
Matrix, inverse of 333
Matrix, orthogonal 340
Matrix, rank of 330 750
Matrix, scalar 329
Matrix, singular 331
Matrix, square 327
Matrix, symmetric 347
Matrix, transpose of 334
Matrix, unit 329
Matrix, unitary 343p 350
Matrix, zero 329
Maxima and minima 246
Maxima and minima, absolute 247
Maxima and minima, constrained 249 269
Maxima and minima, relative 247 (see also “Calculus of variations”)
Maximum modulus theorem 558
Maximum principles 506 507
Maxwell — Boltzmann distribution 633
Mean errors 200 659 660
Mean errors, reliability of estimate of 670
Mean-value theorem for integrals 380
Mean-value theorem of differential calculus 224
Measurable set 773
Measure 772
Measure numbers 291 319
Measure theory 614 772
Mechanics, laws of 302
Median value 637p
Membrane under gas pressure 482p
Membrane, of rectangular 474
Membrane, vibration of circular 480
Metric coefficients 360
Minima see “Maxima and minima”
minimax 249
Minimizing curve 265
Minimum descent, curve of 269p 767
Minimum potential-energy principle 264
Minors of a determinant 741
Modes 477 481
Modulus of a complex number 528
Moment of dipole 497
Moment of force 303
Moment of inertia 274
Moment of momentum 305
Moment, bending 435p
Momentum vector 305
Momentum, angular 305
Momentum, linear 42 44
Momentum, moment of 305
Monte Carlo methods 652
Multiple integrals 270
Multiply connected region 383
| Mutually exclusive events 610 619
Nabla or del,  370 370
Neighborhood of a point 540
Neumann’s function 503
Neumann’s function for hall plane 504
Neumann’s problem 503
Newtonian potential 277p 409
Newton’s interpolation formulas 696
Newton’s law of attraction 46 409
Newton’s Law of Cooling 461
Newton’s law of gravitation 46 408
Newton’s law of motion 12 43
Newton’s method of solving equations 684
Nodal lines 477
nodes 129 415
Normal acceleration 313
Normal derivatives 241 369
Normal distribution 633 651
Normal distribution, bivariate 666
Normal equations 703
Normal law of probability 647
Normal law of probability, intorpretation of 653
Normal line 309 (see also “Normal”)
Normal to a curve 311
Normal to a surface 309 369
Normal, principal 311
Numerical analysis 673—736
Numerical differentiation 698
Numerical integration 715
Numerical solution of differential equations 37 721—736
Odd functions 183
Odd functions, Fourier expansion for 185
Operator,  510 692 510 692
Operator,  370 386 407 692 370 386 407 692
Operator, 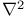 387 387
Operator, curl 398 407
Operator, D 57 430p
Operator, difference 510 692
Operator, div 386 406
Operator, Fourier transform 482
Operator, Laplace 387
Operator, Laplace transform 754
Operator, linear 336 754
Order of differential equations 6 29 76 425
Order, interchange in partial differentiation 221
Order, inversions of 742
Order, reduction of 29 76
Ordinary differential equations 1—106
Ordinary differential equations of electric circuits 81 100 761p
Ordinary differential equations with constant coefficients 54 66 100
Ordinary differential equations with separable variables 18
Ordinary differential equations, Abel’s theorem for 54p
Ordinary differential equations, Bernoulli’s 27
Ordinary differential equations, Bessel’s 159
Ordinary differential equations, boundary-value pioblems in 91 730
Ordinary differential equations, Cauchy’s 78
Ordinary differential equations, Chaplygin’s method for 37
Ordinary differential equations, characteristic equation for 54 67 101
Ordinary differential equations, Clairaut’s 27p
Ordinary differential equations, Euler — Cauchy’s 78
Ordinary differential equations, Euler’s 267
Ordinary differential equations, exact 20
Ordinary differential equations, existence and uniqueness theorems for 5 7 38 157
Ordinary differential equations, first-order 17—50
Ordinary differential equations, Fuchs’ theorem on 157
Ordinary differential equations, Gauss’ hypergeometric 165p
Ordinary differential equations, homogeneous, first-order 18
Ordinary differential equations, homogeneous, linear 51 54 59 96
Ordinary differential equations, homogeneous, systems of 100 733
Ordinary differential equations, hypergeometric 165
Ordinary differential equations, indicial equations for 161
Ordinary differential equations, initial-value problem for 9 90 730
Ordinary differential equations, integral curves for 7
Ordinary differential equations, integrals of 7
Ordinary differential equations, integrating factors for 22
Ordinary differential equations, integration between limits 13
Ordinary differential equations, isoclines for 36
Ordinary differential equations, Lagrange’s 26
Ordinary differential equations, Legendre’s 158
Ordinary differential equations, linear 23 51 59
Ordinary differential equations, linear, complementary function for 59n
Ordinary differential equations, linear, systems of 95 733
Ordinary differential equations, linear, with constant coefficients 54 66
Ordinary differential equations, linear, with variable coefficients 51 59 70 153
Ordinary differential equations, order of 6 425
Ordinary differential equations, reduction of 29 76
Ordinary differential equations, solutions of 6
Ordinary differential equations, solutions of, by Laplace transform 756—768
Ordinary differential equations, solutions of, by numerical methods 37 721—736
Ordinary differential equations, solutions of, by power series 153
Ordinary differential equations, solutions of, general 10 52 59 67 102
Ordinary differential equations, solutions of, linearly independent 7 59 72 76p
Ordinary differential equations, solutions of, particular 7 59 72 76p
Ordinary differential equations, solutions of, singular 8 34
Ordinary differential equations, solutions of, stability of 103 105
Ordinary differential equations, solutions of, uniqueness of 7 38 157
Ordinary differential equations, systems of 95 110 727
Ordinary differential equations, systems of, characteristic equation for 101 733
Origin 288
Orthogonal coordinates 363
Orthogonal curves 31
orthogonal matrices 340
Orthogonal sets of functions 195
Orthogonal sets of functions, completeness and closure of 203
Orthogonal sets of functions, expansion in series of 201
Orthogonal sets of functions, relation of least squares to 202
Orthogonal trajectories 30
Orthogonal transformations 340
Orthogonal vectors 319
Orthogonality weighted 197
Orthogonalization of matrices 340 350
Orthogonalization of vectors 320
Orthonormal functions 195 197
Orthonormal vectors 320
Oscillations of cable 445 454
Oscillations of spring 80 82 86 88 89
Oscillations, damped 449
Oscillations, period of 44 81 84
Osculating plane 311
Parabolic coordinates 408p
Parabolic differential equation 506
Parabolic differential equation, difference equation for 512
Parabolic minor 33
Parallelogram law of addition 288 529
Parseval’s equality 202 204p
Partial differential equations 5 425—521
Partial differential equations of elliptic type 504
Partial differential equations of heat flow 414 455
Partial differential equations of hydrodynamics 416 429
Partial differential equations of hyperbolic type 504 516
Partial differential equations of parabolic type 504 516
Partial differential equations of potential theory 409 411n
Partial differential equations of vibrating membranes 475 480
Partial differential equations of vibrating rods 435p 485p
Partial differential equations of vibrating string 431 484
Partial differential equations of wave motion 428
Partial differential equations, boundary conditions for 443
Partial differential equations, canonical forms of 517
Partial differential equations, characteristic values for 507p
Partial differential equations, characteristics for 441 521
Partial differential equations, solutions of, by Fourier transform 482—490
Partial differential equations, solutions of, by integrals 482—504
Partial differential equations, solutions of, by Laplace transform 769p
Partial differential equations, solutions of, by series 448—482
Partial differential equations, solutions of, fundamental 521
Partial differential equations, solutions of, numerical 734
Partial differential equations, solutions of, uniqueness of 505—510
Partial differentiation 219
Partial differentiation, interchange of order in 221
Partial sum of series 111
|
|
 |
| Реклама |
 |
|
|
 |
 |
|
 |
|
О проекте
|
|
О проекте