|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Sokolnikoff I.S. — Tensor Analysis: Theory and Applications to Geometry and Mechanics of Continua |
|
|
 |
| Предметный указатель |
 -systems 138 152 -systems 138 152
 -systems, derivatives of 140 180 -systems, derivatives of 140 180
 -systems, tensor character of 138 -systems, tensor character of 138
Absolute derivative 132
Absolute tensor 73
Acceleration, of a fluid 322
Acceleration, of a particle 198 263
Action, principle of least 219
Admissible functional arguments 153
Admissible transformations 53
Affine transformation 10 83
Algebra of tensors 66—68
Angle, between coordinate lines 122
Angle, between directions in space 121
Angle, between directions on a surface 149
Anisotropic media 315 318
Appell, P. 81 238 262 290 327
Arc length, along a curve in space 135
Arc length, along a curve on a surface 147
Arc length, along coordinate lines 122
Arc length, element of 75 100 110 119 147 193
Area, element of 151
Associated tensors 70
Axiom, of dimensionality, JI Axiom, of parallels 109
Axioms for linear vector spaces 11
Beltrami, E. 110
Bergmann, P. G. 270 288 289 327
Bernoulli, D. 219
Bertrand, J. L. F. 142
Bianchi’s identities 95
Binormal 138
Birkhoff, G. D. 276 280
Bolyai, J. 0
Bolza, O. 221
Bouquet, J. C. 98
Brillouin, L. 290 327
Calculus of variations 352—159
Calculus of variations, fundamental lemma in 154
Calculus of variations, fundamental problem of 154
Cantor 1
Carath odory, C. 221 odory, C. 221
Cartan, E. 98
Cauchy — Schwarz inequality 194
Cauchy, A. L. 307 318
Cayley, A. 116
Center of mass 258
Characteristic values of matrices 33 37
Chou, P. Y. 280
Christoffel symbols 78
Christoffel symbols, transformation of 82
Christoffel, E. B. 84
Closure, property of 55
Codazzi equations 186
Collar, A. R. 237
Compatibility, equations of 300
Components of tensors 51 62
Components of tensors, laws of transformation for 61—63
Components of vectors 8 13
Components of vectors, physical 8 126
Conservation, of energy 209 218 273
Conservation, of mass 273 317
Conservative force fields 203 218
Continuity, equation of 322
Contraction, in relativity 264
Contraction, of tensors 67
Contravariant and covariant laws 59 62
Contravariant and covariant laws, tensor character of 64
Contravariant transformation 57
Contravariant vector 59
Coordinate curves (or lines) 118
Coordinate surfaces 118
Coordinate systems 1 10
Coordinate systems, construction of 1
Coordinate systems, oblique cartesian 3
Coordinate systems, orthogonal cartesian 3 13
Coordinates, curvilinear 116 143
Coordinates, curvilinear, cylindrical 119
Coordinates, curvilinear, Gaussian 145
Coordinates, curvilinear, generalized 223
Coordinates, curvilinear, geodesic 163
Coordinates, curvilinear, local 268
Coordinates, curvilinear, normal 48
Coordinates, curvilinear, orthogonal 122 150
Coordinates, curvilinear, proper 268
Coordinates, curvilinear, spherical 53 118
Coordinates, curvilinear, transformation of 10 52
Correspondence, one-to-one 1 9
Cosine of an angle 194
Courant, R. 257
Covariant and contravariant laws 59 62
Covariant and contravariant laws, tensor character of 64
Covariant derivative of a tensor 85—87
Covariant differentiation 84—88
Covariant differentiation, formulas for 87
Covariant differentiation, inversion of order of 91 92
Covariant tensor 61
Covariant transformation 57
Covariant vector 59
Cramer’s Rule 19
Curl of a vector, in cartesian coordinates 249
Curl of a vector, in curvilinear coordinates 251
Curvature vector 139
Curvature, Einstein 169
Curvature, Gaussian 168 187
Curvature, geodesic 171
Curvature, lines of 191
Curvature, mean 187
Curvature, normal, of a surface 189
Curvature, of a curve 137
Curvature, radius of 189
Curvature, total 168 187
Curvatures, principal 191
Curve, motion of particle on a 207
Curves, coordinate 118
Curves, in space 135
Curves, on a surface 187
Curvilinear coordinates, in space 116
Curvilinear coordinates, on a surface 143
D'Alembert's principle 309
Darboux, G. 98
Dedekind, J. W. R. 1
Deflection of light rays 288
Deformation, of space 26
Deformation, of space, analysis of 291—296
Deltas, Kronecker 13 19 100 105
Density, scalar 72
Derivative, absolute 132
Derivative, covariant 85 87
Derivative, intrinsic 132
Derivative, of a base vector 129
Derivative, of a tensor 85 87
Derivative, of a vector 85 128
Derivative, of an invariant 86
Derivative, tensor 178
Descartes, R. 1
Determinants 18 105
Determinants, differentiation of 107
Determinants, expansion of 19 106
Determinants, functional 54
Determinants, multiplication of 18 106
Determinants, Vandermondian 34
Dickson, L. E. 34
Differentiation, covariant 84
Differentiation, intrinsic 131
Differentiation, tensor 178
Dilatation 305
Dimensionality of space, axiom for 11
Direction moment 148
Direction, in space 120 194
Direction, on a surface 148
| Displacement vector 4 198 295
Distance, Euclidean 119 193
Distortion of volume elements 303
Divergence of a vector, in cartesian coordinates 247
Divergence of a vector, in curvilinear coordinates 247
Divergence of a vector, in cylindrical coordinates 250
Divergence of a vector, in orthogonal curvilinear coordinates 251
Divergence of a vector, in plane polar coordinates 250
Divergence of a vector, in spherical coordinates 250
Divergence theorem 247
Duncan, W. J. 237
Dynamics, of  particles 223 particles 223
Dynamics, of a particle 199
Dynamics, of rigid bodies 223
Dynamics, relativistic 275
e-systems 100 107 151
e-systems, application of, to determinants 105
Eddington, A. S. 276 288 289 327
Einstein curvature 169
Einstein's energy equation 271
Einstein, A. 61 95 264 265 267 273 275 289
Einstein’s gravitational equations 275
Einstein’s postulates 265
Einstein’s tensor 95
Eisenhart, L. P. 161 166 186 327
Elastic constants 317
Elasticity, equations of 318
Energy 201
Energy, conservation of 209 218 273
Energy, equation of 273
Energy, integral of 218
Energy, internal 315
Energy, kinetic 203
Energy, potential 203
Energy, strain 315
entropy 315
Equilibrium, differential equations of 307
Ether 204
Euclidean space 4 25 75 00 112
Euclid’s axiom of parallels 109
Euclid’s Elements 109
Euler, L. 157 219
Eulerian hydrodynamical equations 324
Eulerian strain tensor 293
Euler’s equations 155—159
Extremals of functionals 153 157 159
Extremum, constrained 159 233
Fermi, E. 165
Field, conservative 203
Field, tensor 63
Field, vector 128
Fitzgerald, G. F. 207
Fluid, incompressible 323
Fluid, perfect 323
Fluid, viscous 320
Flux of a gravitational field 251
force 199
Forces, external and internal 230
Forces, generalized 228
Forces, reactive 230
Forces, workless 230
Frazer, R. A. 237
Free indices 18
Frenot formulas 139—141
Frequency equation 237
Functional 153
Functions, linear vcctor 25
Functions, of class 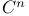 53 53
Functions, scalar point 56
Fundamental quadratic form, first 145 147
Fundamental quadratic form, second 177 181
Fundamental tensor 76
Galilean transformations 263
Galileo 199
Gauss, C. F. 110 143 177 246
Gauss, equation of 186
Gauss, formulas of 183
Gaussian curvature 168
Gauss’ equations of a surface 143
Gauss’ flux theorem 253
Generalized coordinates 223
Generalized force 228
Generalized momentum 239
Generalized velocities 224
Generalized virtual displacements 231
Geodesic coordinates 163—165
Geodesic curvature 171
Geodesics 159 161
Geodesics, trajectories as 229
Geometrization of dynamics 222 229
Geometry, Lobachevskian 115
Geometry, metric 111
Geometry, non — Euclidean 109
Geometry, of space curves 135
Geometry, Riemannian 112
Gravitation, Einstein’s law of 275
Gravitation, Newton’s law of 242
Gravitational field, constant 206
Green, G. 246
Green’s function 256
Green’s theorems 248 256
Griffith, B, A. 238 262
Group, abstract 55
Groups, isomorphic 57
Hamilton, W. R. 199 219
Hamiltonian function 239
Hamilton’s equations 238
Hamilton’s principle 216
Hermitean matrices 48
Hilbert, D. 257
Holonomic systems 225
Hooke’s law 317
Hydrodynamics, equations of 324
Hydrostatic pressure 320
Ideal fluid 323
Incompressible fluid 323
Indices, free 18
Indices, summation 17
Inertial systems 198
Infinitesimal strains 300 318
Inner product of tensors 69
Integrability conditions 98 183 300
interval 269
Intrinsic differentiation 131
Intrinsic geometry 143 145 167
Invariance, concept of 51
Invariance, of physical laws 263
Invariance, transformation by 55
Invariants 52
Invariants, derivatives of 86
Irrotational motion 325
Isometric surfaces 167
Isotropic media 315
Jacobi, C. G. J. 219 221
Jacobian determinants 54
Kellogg, O. D. 246 247
Kepler’s law 242 261
Killing’s equations 311
kinetic energy 203
Kinetic potential 228
Klein, P. 116
Kronecker deltas 13 19 100
Kronecker deltas, derivatives of 108
Kronecker deltas, tensor character of 105
Lagrange, J. L. 199 219
Lagrangean equations of motion 204 221 225
Lagrangean function 205
Lagrangean strain tensor 293
Lam 's constants 317 's constants 317
Landau, L. 289
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -systems
-systems  odory, C.
odory, C.  particles
particles