|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Sokolnikoff I.S. — Tensor Analysis: Theory and Applications to Geometry and Mechanics of Continua |
|
|
 |
| Предметный указатель |
Laplace developments 19
Laplace’s equation 92
Laplacian 248 249
Laplacian, in cartesian coordinates 92
Laplacian, in curvilinear coordinates 92
Laplacian, in cylindrical coordinates 250
Laplacian, in plane polar coordinates 250
Laplacian, in spherical coordinates 93 250
Length, element of 75 100 110
Length, of a vector 11 194
Levi — Civita 165 276 327
Lifshitz, E. 289
Light rays, deflection of 288
Light, velocity of 264 265
Lindsay, R. B. 200 327
Line, straight 142
Line-element, in space 75 100 110
Line-element, on a surface 147
Linear dependence 6 15
Linear dependence, of vectors 6 15
Linear transformations 10 20 25 29
Linear vector spaces, complex 14
Linear vector spaces, real 10
Lobachevskian geometry 135
Lobachevsky, N. 109
Local coordinates 268
Lorentz — Einstcin transformation 267
Lorentz — FitzGerald contraction 264 267
Lorentz, H. A. 264 265 267
Mach, E. 200
Manifold 9
Manifold,  -dimensional 10 193 -dimensional 10 193
Manifold, non — Euclidean 76
Manifold, Riemannian 222
Margenau, H. 200 327
Mass, center of 258
Mass, conservation of 273 317
Mass, gravitational 200
Mass, inertial 199 200
Mass, rest of proper 271
Mass-energy relationship 273
Matrices 16 20
Matrices, algebra of 20—25
Matrices, characteristic equation of 37
Matrices, characteristic values of 33 37 50
Matrices, diagonal 22
Matrices, Herraitean 48
Matrices, inverse 23
Matrices, orthogonal 30
Matrices, rank of 16
Matrices, real symmetric 34
Matrices, reduction to diagonal form 31
Matrices, similar 27 30 38
Matrices, singular 22
Matrices, unitary 48
Maupertuis, P. M. L. 219
McConnell, A. J. 332 178 180 181 184 207 290 327
Mean curvature 187
Measure numbers of a vector 8
Mechanics of a particle 197
Mechanics of fluids 319
Metric geometries 111
Metric space 10 111
Metric tensor 74
Metric tensor, derivatives of 89
Metric tensor, of a surface 147
Michal 3 290 327
Minimum principles 219
Minkowski’s acceleration 269
Minkowski’s velocity 269
Moment of force 243
Momentum 199
Motion of a particle on a curve 207
Motion of a particle on a surface 210
Motion, equations of, for a continuous medium 309
Motion, for a fluid 322
Motion, for a particle 201 271
Motion, irrotational 325
Mousnier’s theorem 189
Murnaghan, JF. D. 34 290 318 327
Natural system 224
Navier equations 319
Navier equations, of fluid motion 322
Navier — Stokes’ hydrodynamical equations 324
Neighborhood of functional arguments 153
Newton, I. 198 199 242 257
Newtonian law of gravitation 242
Newtonian laws 198
Non-holonomic systems 225 232
Normal coordinates 48 236
Normal curvature, of a surface 189
Normal curvature, principal 191
Normal line to a surface 175
Normal modes of vibration 48
Normal vector, to a curve 136
Normal vector, to a surface 176
Normal vector, to a surface curve 171
Oontravariant tensor 60
Ortho-normal systems of vectors 8 11 13
Orthogonal curvilinear coordinates, condition for 122
Orthogonal transformations 27 30
Orthogonality of vectors 11 30 150
Osculating plane 137
Parallel postulate 109
Parallel vector fields, along a curve 133
Parallel vector fields, along a surface curve 165
Parallelism of vectors 166
Parallelogram law of addition 4
Particles, dynamics of 199
Particles, free moving 206
Particles, relativistic dynamics of 275
Pendulum, double 235
Pendulum, simple 206 233
Pendulum, spherical 238
Perihelion constant 262
Perihelion of Mercury 284 287
Perihelion, advance of 285
Physical components of a vector 8 126 205
Planetary orbits 280
Poincare, II. 116 265
Poisson’s equation 246 254
Poisson’s ratio 317
Potential functions 275
Potential, clastic 315
Potential, gravitational 245
Potential, velocity 325
Primary inertial system 198
Principal curvatures of a surface 190
Principal directions of strain 302
Principal directions of stress 307
Principal directions on a surface 191
Principal normal vector 137
Principal radii of a surface 192
Principal strains 303
Principal stress 307
Principle of least action 219
Problem of two bodies 257
Proper mass 271
Pythagoras, formula of 3 13
Quadratic forms 35
Quadratic forms, characteristic values of 33 37 47
Quadratic forms, classification and properties of 44
Quadratic forms, index of 45
Quadratic forms, rank of 45
Quadratic forms, reduction of 35 40 46
Quadric of Cauchy, strain 302
Quadric of Cauchy, stress 307
Quadric, canonical form of 45
Quotient laws of tensors 68
Rainich, G. Y. 276 287 288 289 327
| Rank of a tensor 61
Rapidity 268
Reciprocal base systems 126
Relative scalar 72
Relative tensors 72 107
Relativistic dynamics 275
Relativity, general theory of 275—289
Relativity, restricted theory of 264—274
Ricci tensor 94
Ricci, G. 61
Ricci’s identity 92
Ricci’s theorem 89
Rice, J. 89
Riemann — Christoffel tensor 89 91
Riemann — Christoffel tensor, properties of 93
Riemannian geometry 112
Riemannian space 96 112
Riemann’s dissertation 110
Rigid body displacements 293
Rigid virtual displacement 311
Riz, P. 318
Robertson, H, P. 289
Saint Venant, B. 300
Savile, H. 109
scalar 56
Scalar density 72
Scalar product 5 14 121
Scalar product, triple 126
Schild, A. 327
Schr dinger, E. 289 dinger, E. 289
Schwarzschild, K. 276
Schwarzschild’s line element 280
Serret — Frenet formulas 139
Seugling, W. R. 301
Shearing strains 298
Shears 307
Similar transformations 27
Skew-symmetric systems 101
Skew-symmetric tensors 71
Small oscillations 236
Sokolnikoff, I. S. 53 246 300 318 327
Space curves, geometry of 135
Space, dimensionality of 6 9
Space, Euclidean 4 96
Space, metric 10 111
Space, Riemannian 96
Space-time manifold 265
Spaces,  -dimensional 9 10 -dimensional 9 10
Spaces, complex linear vector 14
Spaces, Euclidean 4 39
Spaces, linear vector 6
Spaces, non — Euclidean 76
Spectral lines, shift of 288
Spherically symmetric static field 277— 280
Stakgold, I. 318
State, equation of 322
Stevinus, S. 4
Stokes, G. G. 246 323
Stokes’ Theorem 249
Straight line, equation of 142
Strain invariants 303
Strain quadric 301
Strain tensor 293
Strain, in cartesian coordinates 296
Strain, infinitesimal 300
Strain, physical components of 296
Strain, principal directions of 302
Strain, velocity 321
Stress invariants 307
Stress quadric 307
Stress tensor 306
Stress tensor, symmetry of 309
Stress vector 305
Stress, analysis of 305—307
Stress, principal 307
Stress, types of 307
Stress-strain relation 316
Summation convention 17
Surface tensors 173
Surface, curves on 146
Surface, element of 151
Surface, equations of 143
Surface, fundamental forms for 147
Surface, imbedded in 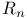 195 195
Surface, intrinsic geometry of 145
Surface, particle on a 210
Surfaces, coordinate 118
Surfaces, in space 171
Surfaces, isometric 167
Symmetric systems 100
Symmetric tensors 71
Synge, J. L. 238 262 289 327
Tangent vector, to a space curve 136
Tangent vector, to a surface 175
Tangent vector, to a surface curve 165
Tensor concept 60
Tensor derivatives 178
Tensor equations 66
Tensor fields 63
Tensors, absolute 73
Tensors, algebra of 66—68
Tensors, associated 76
Tensors, calculus of 84 89
Tensors, components of 51 62
Tensors, contraction of 07
Tensors, contravariant 62 03
Tensors, covariant 61 62
Tensors, covariant differentiation of 85—87
Tensors, fundamental 76
Tensors, intrinsic differentiation of 131
Tensors, metric 74
Tensors, mixed 03
Tensors, quotient laws for 68
Tensors, rank of 62
Tensors, relative 72
Tensors, Riemann — Christoffel 89 91
Tensors, symmetric and skew-symmetric 71
Tensors, tensor differentiation of 178
Tensors, types of 014 3
Thomas, T. Y. 98 327
Time 197 203 205
Tolman, R. 207 289
Torsion 138
Total curvature 108 187
Trajectories as geodesies 229
Trajectory, of a dynamical system 228
Trajectory, of a particle 201
Transformation theorems 210—250
Transformations, admissible 53
Transformations, affine 10 25
Transformations, by contravariance 57
Transformations, by covariance 57
Transformations, by invariance 55
Transformations, functional 52
Transformations, Galilean 203
Transformations, induced 60
Transformations, linear 10 25 29
Transformations, of coordinates 10 52 145
Transformations, of rotation 29
Transformations, orthogonal 27
Transformations, similar 27 30
Transformations, unitary 48
Unitary transformations 48
Vandermondian determinant 34
Variation, of strain tensor 313
Variation, symbol of 213—216
Variation, symbol of, of function 156 310
Variation, symbol of, of integral 157
Varied path 214
Veblen, O. 9 61 327
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -dimensional
-dimensional  dinger, E.
dinger, E.