|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Brocker Th., Dieck T.T. — Representations of Compact Lie Groups |
|
|
 |
| Предметный указатель |
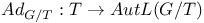 49 160 49 160
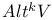 (alternating k-forms) 41 (alternating k-forms) 41
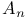 (Dynkin diagram) 212 216 218 (Dynkin diagram) 212 216 218
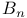 (Dynkin diagram) 212 216 220 (Dynkin diagram) 212 216 220
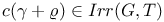 241 241
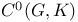 as a representation 123 ff as a representation 123 ff
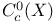 40 40
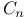 (Dynkin diagram) 212 216 221 (Dynkin diagram) 212 216 221
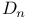 (Dynkin diagram) 212 216 219 (Dynkin diagram) 212 216 219
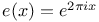 240 240
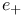 , , 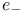 , , 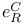 , , 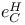 , , 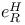 94f 94f
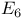 , , 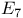 , , 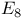 (Dynkin diagram) 212 216 (Dynkin diagram) 212 216
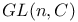 , , 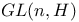 , , 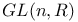 3 7 3 7
 (Dynkin diagram) 212 216 227 (Dynkin diagram) 212 216 227
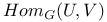 67 67
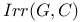 , , 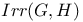 , , 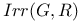 69 96 69 96
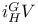 : induced representation 143 : induced representation 143
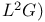 square-integrable functions 134 square-integrable functions 134
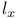 : left translation 14 : left translation 14
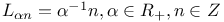 226 226
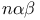 (Cartan number) 198 ff (Cartan number) 198 ff
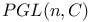 , , 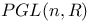 4 11 4 11
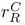 , , 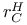 , , 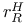 , , 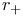 , , 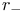 95 95
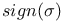 41 41
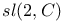 115 ff 196 202 115 ff 196 202
 , , 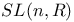 4 4
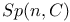 9 155 9 155
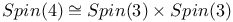 292 292
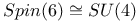 292 292
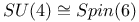 292 292
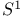 (circle) 3 (circle) 3
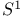 , representations 125 , representations 125
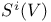 (symmetric power) 75 (symmetric power) 75
 (sphere) 36 (sphere) 36
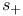 , , 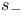 94 94
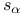 (reflection ass. to \alpha\in R) 192 197 (reflection ass. to \alpha\in R) 192 197
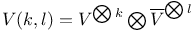 137 137
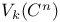 , , 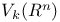 37 f 37 f
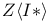 257 257
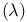 (alternating sum) 240 (alternating sum) 240
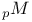 , , 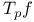 : tangent space 11 ff : tangent space 11 ff
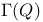 (Clifford group) 57 (Clifford group) 57
 -ring 104 -ring 104
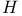 5 5
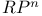 (projective space) 11 (projective space) 11
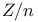 : cyclic group 10 : cyclic group 10
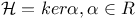 192 198 192 198
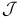 (real or qualernionic structure) 93 (real or qualernionic structure) 93
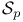 (algebra of germs) 12 169 (algebra of germs) 12 169
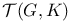 (representative functions) 125 ff (representative functions) 125 ff
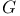 : harmonic polynomials 88 : harmonic polynomials 88
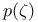 (decomposition into positive roots) 257 (decomposition into positive roots) 257
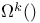 (alternating differential forms) 42 (alternating differential forms) 42
A(n) (alternating group) 10
Abelian Lie group 25 30 39
Abelian Lie group, representations 69 107
Abelian subalgebra, maximal 188
Abstract subgroup 28
Action of a group on a space 30 ff
Ad, ad: adjoint representation 18
Adams operation 104 ff
Adjoint representation 18 71 183 222
Affine variety 152
Affine Weyl group: extended Weyl group 226
Alcove 226
Algebra, associative 54
Algebra, Clifford 54
Algebra, Lie 14 ff 19 20
Algebraic group 156
Alternating 41 240 244
Alternating group 10
Alternating sum 240
Alternating tensor 77
Analytic structure on Lie groups 138
Angle of roots 199 205
Angular velocity 22
Anti-automorphism 6 55
Antipodal map 52
Ascoli 130
Atlas bundle 33
Atlas manifold 2 43
Aut(V) 3
Base space 32
Basis of root system 204
Borel — Weil — Bott theorem 256
Boundary of manifold 50
Bounded operator 130
Bundle 32 188
Bundle atlas 33
Bundle chart 32
Bundle chart, tangent 14
Bundle map 32
C(Q), 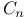 : Clifford algebra 55 : Clifford algebra 55
Canonical decomposition of representation 70 101
Canonical metric of root system 213 215f
Cartan composite 253 262
Cartan matrix 210
Cartan matrix, determinant 216
Cartan number 198
Cartan subgroup 176 ff 297
Casimir operator 122
Center 165 189 201 229 235
Center of 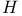 5 11 5 11
Central element 230
centralizer 165 169 189
Chamber 192 227
Change of coordinates 2
Character of a representation 80 ff 107
Character of a representation, formula 239 ff
Character of a representation, group 82 83 107
Character of a representation, ring: representation ring 102 ff
Chart domain 2
Chart of bundle 32
Chart, manifold 2
Class function 81 134 166
Classical groups 1 ff 169
Classical groups, complexification 155
Classical groups, definitions 4 ff
Classical groups, maximal torus 169 ff
Classical groups, representations 265 IT
Classical groups, root systems 216 ff
Classical groups, Weyl groups 169 ff
Clebsch — Gordan formula 87 92 260
Clifford algebra 7 54 283
Clifford algebra, classification 286 291
Clifford algebra, modules 287 f
Clifford group 57
Coassociative 147
Codimension 27
Coinverse 146
Compact group, structure 232 ff
Compact operator 130 ff
Compact scmisimplc Lie algebra 209
Compact-open topology 142
Complex root: root 185
complex type 97
Complexification 151 ff
Comultiplication 146
Con(G) (conjugation classes) 166
Conjugate elements in G and T 166 180
Conjugate homomorphisms 67
Conjugate representations 75
Conjugate tori 159 ff
Conjugation 95
Conjugation in Clifford algebra 57
Conjugation of quaternions 6
Conjugation, complex 75
Conjugation, theorem for tori 159 ff 177
Connected component of unit 10
Contained (a representation in another) 69
| Conv(A) 250
Convolution 67 83 129 139
coordinates 2
Counit 146
Cover, covering 54 228 233
Coxeter graph 211
Cyclic group 10 129 180
Cyclic group, representations 108 129
Cyclic, topologically 38 40 177
C[G]: group ring 66
Decomposable 204
Decomposition into positive roots 257
deg(f) (mapping degree) 51
Derivation 12
Descending chain of manifolds 136 138
Determinant, Cartan matrix 216
Determinant, conjugation map 161 242
Diagonal action 82
Diffeomorphism 40
Differentiable 2 15 41
Differentiable bundle 33
Differentiable G-space 31
Differentiable manifold 2
Differentiable map of manifolds 2
Differential 12
Differential form 41 ff
Dimension of manifold 2
Dimension of representation 65 242 249
Dirac approximation 135 143
Dirac matrix 292
Direct product 3 82 105
Direct sum 69 72 74
Discrete normal subgroup 10 26
Divisible group 25 169
Division algebra 5
Domain of chart 2
Dominant weight 249 ff
Dual representation 75
Duality (Tannaka — Krein) 146
Dynkin diagram 209 ff
Dynkin diagram, classification 212
Elementary symmetric function 175
Embedding 28
Embedding, equivariant 138 143
End(V) 3 99
Equicontinuous 130
Equivalent representations 67
Equivariant 31
Euclidean scalar product 4
Euler angles 53
Euler operator 122
Exponential map 17 21
Exponential map, surjectivity 24 30 165
Extended Weyl group 226
Extension 95
Exterior derivative 50
Exterior power 75 103 175
Exterior product 42
Extremal point 256
Factorial 249
Faithful 66 136
Fiber 32
Fibered product 90 110
Filtration of Clifford algebra 62
Fixed point 31 77 181
Flow 16 39
Frame 37
Frobenius reciprocity 127 144 295
Frobenius theorems 9 234
Fubini 49
Fundamental group 54 61 223
Fundamental representation 254
Fundamental system of weights 254
Fundamental Weyl chamber 204
G-manifold 31
G-space 30 ff
General element of a Lie group 168 181
General position 231
Generator of a torus 38
Germ 12 169
Global root 185 189 195
Global weight: weight 108
Graded 56
Gram — Schmidt orthogonalization 11
Grassmann manifold 38
Group ring 66 83 129
H(G) 264 277
Half sum of positive roots 207 241
Half-space 206
Half-spin representation 279 ff
Half-spin representation, type 290
Harmonic polynomial 88 ff 117
Hermitian 4 21 153
Higher (order on LT*) 250
Hom(U,V) 75
Homogeneous polynomial 84 117
Homogeneous space 30 ff 35
Homomorphism of Lie groups 2 29
Homotopic 51 53 179
Homotopy group 36 f 187 223
Hopf algebra 147
Hopf deration 37 40
I: integral lattice 195
Immersion 27 40
Indecomposable 204 254
Index of self-conjugate irreducible representation 262
Induced representation 143 ff 256 292
Infinitesimal weight 112 ff
Initial value of integral curve 16
Inner product 4 8 9 79 245
Integral (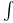 ) 40 ff 44 48 139 ) 40 ff 44 48 139
Integral (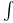 ) curve 16 ) curve 16
Integral (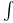 ) formula, Weyl’s 163 ) formula, Weyl’s 163
Integral (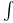 ) on LT 245 ) on LT 245
Integral ( ) elements of LT 195 ) elements of LT 195
Integral ( ) form 195 ) form 195
Integral ( ) lattice 195 221 230 ) lattice 195 221 230
Intertwining operator 67
Invariant 15 31
Invariant inner product 68 92 114
Invariant integral 40 ff 139
Invariant integral of SO(3) 53
Invariant subspace 31
Invariant vector field 15
Inverse root 195 198 208 223
Irr(G,T) 242
Irreducible character 80
Irreducible module 72 287
Irreducible representation 68 141
Irreducible root system 211
Isomorphism of G-modules 67
Isomorphism of Lie groups 2 22
Isotropy group 31 35 138
Isotropy group in Weyl group 202
Isotypical 70 73 83 101 126 128
j (quaternion) 5 62
J (symplectic form) 9
Jacobi identity 19
Jacobian determinant 41
Jacobian matrix 14
k (quaternion) 6 62
Killing form 209 214 229
Kostant’s formula 258
Krein 146
Kronecker product 75
Kronecker theorem 38
L(G): Lie algebra 14
L(G/T) = LG/LT 160
Laplace operator 88
Largest root 257
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



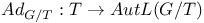
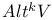 (alternating k-forms)
(alternating k-forms) 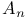 (Dynkin diagram)
(Dynkin diagram) 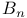 (Dynkin diagram)
(Dynkin diagram) 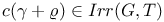
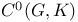 as a representation
as a representation 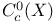
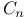 (Dynkin diagram)
(Dynkin diagram) 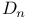 (Dynkin diagram)
(Dynkin diagram) 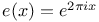
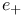 ,
, 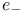 ,
, 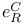 ,
, 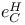 ,
, 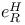
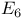 ,
, 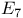 ,
, 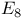 (Dynkin diagram)
(Dynkin diagram) 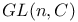 ,
, 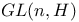 ,
, 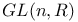
 (Dynkin diagram)
(Dynkin diagram) 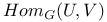
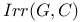 ,
, 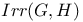 ,
, 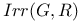
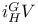 : induced representation
: induced representation 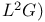 square-integrable functions
square-integrable functions 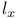 : left translation
: left translation 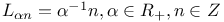
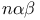 (Cartan number)
(Cartan number) 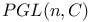 ,
, 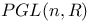
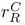 ,
, 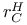 ,
, 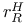 ,
, 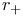 ,
, 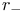
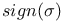
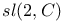
 ,
, 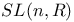
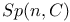
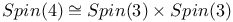
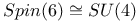
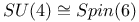
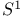 (circle)
(circle) 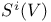 (symmetric power)
(symmetric power)  (sphere)
(sphere) 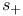 ,
, 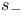
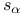 (reflection ass. to \alpha\in R)
(reflection ass. to \alpha\in R) 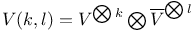
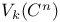 ,
, 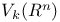
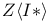
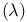 (alternating sum)
(alternating sum) 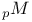 ,
, 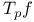 : tangent space
: tangent space 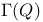 (Clifford group)
(Clifford group)  -ring
-ring 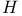
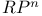 (projective space)
(projective space) 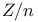 : cyclic group
: cyclic group 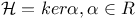
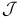 (real or qualernionic structure)
(real or qualernionic structure) 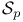 (algebra of germs)
(algebra of germs) 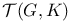 (representative functions)
(representative functions) 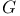 : harmonic polynomials
: harmonic polynomials 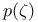 (decomposition into positive roots)
(decomposition into positive roots) 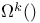 (alternating differential forms)
(alternating differential forms) 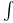 )
)  ) elements of LT
) elements of LT