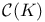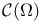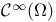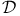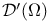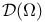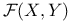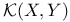|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Fabian M.J., Hajek P., Pelant J. — Functional Analysis and Infinite-Dimensional Geometry |
|
|
 |
| Предметный указатель |
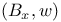 73 75 414 415 73 75 414 415
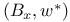 71—73 319 365 395 409—412 71—73 319 365 395 409—412
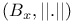 2 14 2 14
 -net 30 -net 30
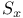 2 2
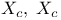 39 39
Annihilator 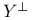 and and 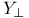 40 55 58 93 148 149 40 55 58 93 148 149
Banach limit 62
Basis, algebraic 34 191
Basis, Auerbach 139 164
Basis, bimonotone 191
Basis, block 172
Basis, boundedly complete 166—168 182 192
Basis, constant 163 169 182
Basis, equivalent 169—171
Basis, Hamel see “Basis: algebraic”
Basis, Markushevich 188—190 382 410—412
Basis, Markushevich, shrinking 188 197 369 370
Basis, Markushevich, weakly compact 364
Basis, Markushevich, weakly Lindeloef 411
Basis, monotone 163 191 192
Basis, normalized 163
Basis, orthonormal 18 20 222
Basis, Schauder 161 163 165 303 307
Basis, seminormalized 303
Basis, shrinking 166—168 184 192 260
Basis, summing 165 181
Basis, unconditional 180 181 196 197
Bump see “”Function”
Cardinality card(A) 23 403
Closure 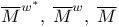 64 64
Compact, Corson 409—412 427 428
Compact, countable 345 399 420
Compact, Eberlein 365 367 388 390—393 409 417 419 420
Compact, scattered 398—401 419 420
Compact, uniform Eberlein 394 395 418 419
Complement 137 138 147—149
Complement, algebraic 137 147
Complement, orthogonal 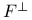 17 18 138 17 18 138
Complement, quasicomplement 377
Constant, basis 163 169 182
Conv(M) 2 22 85 92 104
Convergence, in norm 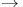 65 65
Convergence, pointwise 66 68 86
Convergence, weak 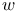 65 86 87 105 65 86 87 105
Convergence, weak star 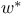 65 87 105 65 87 105
coordinates 161
Decomposition method 140 174
Density dens(X) 358 359 381 382 397 424
Derivative, Cantor 398
Derivative, directional 241
Derivative, Frechet 241 307
Derivative, Gateaux 241
Dirac measure 48 78
Distance, Banach — Mazur 283
Distributions 116 133
Domain Dom(f) 317
Dual see “Operator” “Space”
Embedding, canonical  63 63
Epigraph Epi(f) 317
Equality, parallelogram 17 29
Equality, Parseval 20
Equality, polarization 17
Ext(C) 76 78 80 123
Form, bilinear 158
Form, n-linear 313
Form, quadratic 159
Form, symmetric 313
Fourier coefficient/series 19
Function, 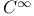 -smooth 314 -smooth 314
Function, 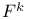 -smooth 314 -smooth 314
Function, 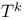 -smooth 340 -smooth 340
Function, 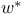 -differentiable 333 334 -differentiable 333 334
Function, bump 314 315 317—319 321 340 342 345 346 424
Function, C-smooth 241
Function, conjugate 321 347
Function, convex 242 247 253 263 265 320
Function, depends on finitely many coordinates 343
Function, Frechet differentiate 241 242 251 253 254 263 320
Function, Gateaux differentiate 241 247 263
Function, inf convolution 265
Function, proper 317
Function, UF 289
Function, UG 289
Functional, biorthogonal 139 164 192
Functional, coordinate 164 171 193 197
Functional, Dirac 48 78
Functional, from X** 69 127
Functional, linear 11 37 38
Functional, Minkowski 42 54
Functional, sublinear 37
Functional, supporting 40 242
Halfspace 64
Homeomorphism 25
Homeomorphism, Lipschitz 331 334 349
Homeomorphism, uniform 133 352 354
Hyperplane 53 76 153
Inequality, Bessel 20
Inequality, Cauchy — Schwarz 3 16
Inequality, Holder 3
Inequality, Khintchine 178
Inequality, Minkowski 4
Inequality, Simons 80
Inequality, triangle 1
Inner product 16
Int(M) 31
James boundary 79 343 344 355
Kernel Ker(T) 11 58 93 208 217
Kronecker 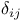 139 139
Lipschitz see “”Homeomorphism” “Map”
Local base 107
Map, affine 102
Map, contraction 227 237
Map, differentiation 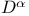 113 116 113 116
Map, fixed point 227
Map, homeomorphism 25
Map, identity 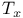 11 11
Map, Lipschitz 10
Map, nonexpansive 227 237
Map, open 49 50
Map, retract 239
Metric, translation invariant 108
Minkowski 42 54
Modulus, of convexity 285 289
Modulus, of rotundity 285 289
Modulus, of smoothness 288 289
Net 65
Net, Cauchy 109
Norm 1
Norm, 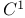 -smooth 241 244 -smooth 241 244
Norm, 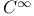 -smooth 314 344 345 421 -smooth 314 344 345 421
Norm, attaining 40 83 102 260 262
Norm, dual 96 245 246 249 280
Norm, equivalent 11 12 25 55
Norm, Frechet differentiate 242—244 249 250 253 254 259 260 267 271 328 367 369
Norm, Gateaux differentiate 242 243 246 247 250 264 275 276 367 382
Norm, LUR (locally uniformly rotund) 248—250 253 271 277 280 281
Norm, operator see “Operator”
Norm, rotund 246 277 281 305
Norm, strictly convex 246 277 281 305
Norm, UC (uniformly convex) 285 287 290 291 293 294 301 303 305 306 308
Norm, UF (uniformly Frechet) 288—291 293 294 304 306 307
Norm, UG (uniformly Gateaux) 289 395 397
Norm, uniformly smooth 288 290 291 293 294 304 306 307
Norm, UR (uniformly rotund) 285 287 290 291 293 294 301 303 305 306 308
Norm, URED 307 308
Norm, WUR 397
Operator, absolutely summing 372—375
Operator, adjoint T* 217
Operator, bounded 10 11 90
| Operator, compact 175 194 203 207—209 215 216 222 223 226 230 232 372
Operator, completely continuous 206 232 375
Operator, Daugavet 310
Operator, dual 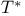 51 58 60 90 207 212 371 51 58 60 90 207 212 371
Operator, eigenspace 214 216
Operator, eigenvalue 214—216 222
Operator, eigenvector 214 221 222
Operator, finite-rank 152 203
Operator, Fredholm 209
Operator, Hilbert — Schmidt 236
Operator, invertible 50 210 211 213
Operator, isometry 11 25 60 90 224
Operator, isomorphism 11 50 60 90 349
Operator, isomorphism into 11 25 59
Operator, norm 11 51 218
Operator, normal 224 226
Operator, on 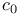 157 175 176 195 196 233 274 364 365 384 157 175 176 195 196 233 274 364 365 384
Operator, on 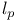 59 90 98 157 175 195 196 232 274 59 90 98 157 175 195 196 232 274
Operator, onto 50 59
Operator, resolvent 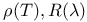 211 223 211 223
Operator, self-adjoint 217—223
Operator, spectral decomposition 223 226
Operator, spectral radius r(T) 213
Operator, spectrum, 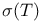 211 212 216 217 219 220 222 234 211 212 216 217 219 220 222 234
Operator, spectrum, approximate 310
Operator, strictly singular 175 194 195 235
Operator, unitary 224
Operator, weakly compact 370—372 383
Partition of unity 328
Point, 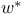 -strongly exposed 278 -strongly exposed 278
Point, cluster 65
Point, diametral 274
Point, exposed 255 276
Point, extreme 76 98 121 276
Point, strongly exposed 255 256 262 277
Polar, 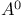 and and  118 133 118 133
Polarization identity 17
Polynomial 313
PRI 359 382 383
Projection 137 147
Projection, canonical 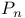 161 163 165 260 161 163 165 260
Projection, Dixmier's 148
Projection, orthogonal 225
Property, approximation 192 205
Property, Banach — Saks 89
Property, C 405—407 410 411
Property, CCC 391 392 401
Property, drop 272
Property, Dunford — Pettis 375—377
Property, Grothendieck 195 383
Property, Heine — Borel 114
Property, Kadec — Klee 280 415
Property, lifting 141
Property, Mazur 383
Property, Schur 146 156
Property, three-space 24 97 405 408
Property, w*-Kadec — Klee 280
Rademacher functions 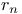 177 177
Seminorm 37 54
Sequence, basic 169 170
Sequence, basic, equivalent 169—171
Sequence, basic, unconditional 181
Sequence, block basic 172 173
Sequence, bounded 6
Sequence, Cauchy 6
Sequence, weakly Cauchy 145
Series, absolutely convergent 8 27 373
Series, unconditionally convergent 27 186 301 373
Set, balanced 108
Set, bounded 10 69 110
Set, closed 70 118
Set, compact 32 345 387 389 393
Set, convex 22 32 70 118 256 259 326
Set, convex, w-closed 70 118
Set, convex, w-compact 84 279
Set, countably compact 128 130 387
Set, cozero 393
Set, dense 14
Set, fragmented 417
Set, generates space 357
Set, index 65
Set, norming see “Subspace”
Set, orthonormal 18
Set, point-finite 393
Set, pointwise bounded 68
Set, polar see “Polar 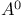 and and  ” ”
Set, relatively w-compact 128 371
Set, saturated family 119
Set, separated 30 54
Set, separating 93 134
Set, sequentially closed 127
Set, sequentially compact 85 128 130 387 419
Set, totally bounded 110
Set, w*-closed 125 189
Set, w*-compact 92 104 11& 382
Set, w-compact 74 84 85 130 255 258 367 387 418
Slice 77
Space, ![$C[0,{w}_{1}]$](/math_tex/7378d3dbcd50fc8f1ce27a62226bd1d582.gif) 406 426—428 406 426—428
Space, 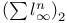 103 193 291 294 103 193 291 294
Space, ![${C}^{n}[0,1]$](/math_tex/40bc1d597d54b957f638c4b4fc8f39a682.gif) 24 154 24 154
Space, ![${C}^{\infty}[0,1]$](/math_tex/76d3da3de653ac289f5a3e38b1736dce82.gif) 133 133
Space, 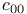 6 6
Space, 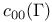 7 7
Space, 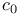 6 14 24 31 44 55 60 74 89 97 99 103 142 143 153—157 164 173 174 180 182 185—187 193 195 205 233 267 269 274 276 280 291 306 331 343 345 355 358 375 377 380 381 383 401 415 421 6 14 24 31 44 55 60 74 89 97 99 103 142 143 153—157 164 173 174 180 182 185—187 193 195 205 233 267 269 274 276 280 291 306 331 343 345 355 358 375 377 380 381 383 401 415 421
Space, 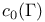 7 45 56 307 358 364 365 378 381 384 394 7 45 56 307 358 364 365 378 381 384 394
Space,  44 55 56 88 98 103 140 141 146 155 157 184 185 187 196 232 268 274 306 336 356 375 415 44 55 56 88 98 103 140 141 146 155 157 184 185 187 196 232 268 274 306 336 356 375 415
Space, 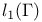 56 156 267 358 367 400 56 156 267 358 367 400
Space, ![${L}_{1}[0,1]$](/math_tex/5ae6f33bdf4b2a81dc578db48c39f4cc82.gif) 22 47 99 183 276 358 385 22 47 99 183 276 358 385
Space, 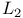 15 20 21 31 88 89 98 155 177 193—195 233 306 353 384 385 15 20 21 31 88 89 98 155 177 193—195 233 306 353 384 385
Space, ![${L}_{2}[0,1]$](/math_tex/60d24fdb53de1939e76576283bacf6d982.gif) 21 206 21 206
Space, 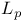 4—6 14 22 23 31 35 45 74 97 131 153 158 159 164 173—175 180 193 195 205 306 336 341 342 385 4—6 14 22 23 31 35 45 74 97 131 153 158 159 164 173—175 180 193 195 205 306 336 341 342 385
Space, 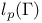 7 45 56 155 195 347 7 45 56 155 195 347
Space, 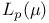 10 286 290 10 286 290
Space, ![${L}_{p}[0,1]$](/math_tex/dba7b5b94f8fef3ad086911096cb330582.gif) 8 15 22 23 45 74 112 154 177 180 193 268 302 8 15 22 23 45 74 112 154 177 180 193 268 302
Space, 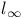 3 6 14 15 22—24 44 62 88 95 99 141—143 155 156 187 189 190 194 196 268 346 347 358 377 380 382—384 424 3 6 14 15 22—24 44 62 88 95 99 141—143 155 156 187 189 190 194 196 268 346 347 358 377 380 382—384 424
Space, 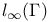 7 155 378 7 155 378
Space, ![${L}_{\infty}[0,1]$](/math_tex/5b640a8d1b661afc3b3f10e5032a0e7d82.gif) 10 15 22 47 99 194 268 10 15 22 47 99 194 268
Space, 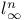 306 306
Space, 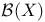 11 11
Space, 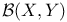 414 415 414 415
Space, 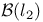 15 233 235 15 233 235
Space, 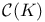 3 48 60 72 78 79 99 345 376 387 389 392 394 395 400 401 420 421 3 48 60 72 78 79 99 345 376 387 389 392 394 395 400 401 420 421
Space, 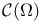 113 113
Space, 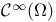 113 113
Space, 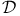 408 408
Space, 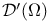 see “Distributions” see “Distributions”
Space, 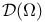 114 114
Space, 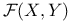 203 205 203 205
Space, 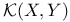 203 205 203 205
Space, (co)type 30 306
Space, angelic 129 130 365 427
Space, Asplund 254 318 397 400
Space, Banach space 1 8
Space, C 6 14 56 99 100 153 154
Space, complete 109 132
Space, complex 39
Space, countable tightness 129
Space, C[0,1] 2 15 47 48 60 74 89 99 144 145 153 164 192 193 195 240 267 273 274 276 288 310 376 377 385
Space, direct sum 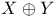 11 138 149 11 138 149
Space, direct sum 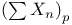 56 271 306 381 56 271 306 381
Space, direct sum 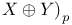 13 149 13 149
Space, dual 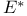 111 111
Space, dual 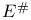 117 117
Space, dual 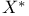 38 41 167 253 38 41 167 253
Space, dual second 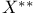 63 63
Space, finite-dimensional 12 31 52 66 109 111 263 264 305 306 334
Space, finitely representable 291 293 306 333
Space, fragmented 417
Space, Frechet 108 129
Space, generated by K 357
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



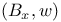
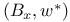
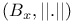
 -net
-net 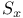
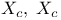
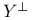 and
and 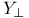
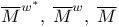
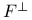
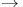
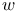
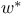

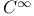 -smooth
-smooth 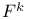 -smooth
-smooth 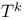 -smooth
-smooth 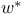 -differentiable
-differentiable 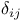
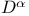
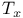
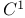 -smooth
-smooth 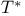
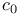
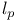
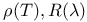
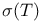
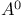 and
and 
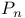
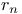
![$C[0,{w}_{1}]$](/math_tex/7378d3dbcd50fc8f1ce27a62226bd1d582.gif)
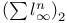
![${C}^{n}[0,1]$](/math_tex/40bc1d597d54b957f638c4b4fc8f39a682.gif)
![${C}^{\infty}[0,1]$](/math_tex/76d3da3de653ac289f5a3e38b1736dce82.gif)
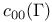
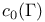

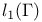
![${L}_{1}[0,1]$](/math_tex/5ae6f33bdf4b2a81dc578db48c39f4cc82.gif)
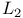
![${L}_{2}[0,1]$](/math_tex/60d24fdb53de1939e76576283bacf6d982.gif)
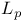
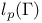
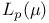
![${L}_{p}[0,1]$](/math_tex/dba7b5b94f8fef3ad086911096cb330582.gif)
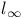
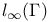
![${L}_{\infty}[0,1]$](/math_tex/5b640a8d1b661afc3b3f10e5032a0e7d82.gif)