|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Fabian M.J., Hajek P., Pelant J. — Functional Analysis and Infinite-Dimensional Geometry |
|
|
 |
| Предметный указатель |
Space, Hilbert 17 20 30 48 140 196 267 277 293 333 340 355
Space, homeomorphic 25 199 337 351 353
Space, infinite-dimensional 14 52 373
Space, injective 142 154
Space, isometric 11
Space, isomorphic 11 307
Space, James 7 185 198
Space, James tree JT 199
Space, Lindeloef 404
Space, Lipschitz equivalent 331 333
Space, locally convex 108
Space, metric 145 233 331 365 418 420
Space, metrizable 71 72 110 390 391 393 399 421 428
Space, normable 108 111
Space, normed 1
Space, Polish 414
Space, pseudocompact 412
Space, quotient X/Y 12 41 96 138 271 306
Space, real 39
Space, reflexive 74 75 84 97 136 168 185 189 244 276 278 291 295 337 357 367 370 372 376 377 384
Space, saturated 343 345 401
Space, second dual X** 69 82 167 275 291
Space, separable 14 26 41 55 71—73 75 82 94 95 140—142 144 182 184 190 197 244 247 248 250 251 253 256 275 280 308 314 328—330 337 345 348 353 357 377 391 410 412 425 428
Space, sequentially compact 85
Space, sequentially complete 196
Space, Sobolev ![${W}_{p}^{k}[0,1]$](/math_tex/d454920100c3a3ea59de1daef2758c3e82.gif) 133 133
Space, superreflexive 294 303 307 315 328 333
Space, topological vector 107
Space, totally incomparable 175 192
Space, Tsirelson T 311
Space, uniformly homeomorphic 133
Space, WCD 383
Space, WCG 357—359 364—367 369 377 379—383 392 405 408 409 418 428
Space, weak Asplund 248
Space, weakly Lindeloef 404 405 408—411
Span(M) 2 22
Subdifferential 321
Subdifferential, Frechet 320 321
subspace 2 41 75
Subspace, affine 76
Subspace, complemented 137—139 142 147—149 152 350 376 377
Subspace, finite-dimensional 13 109 139
Subspace, invariant 215 221 230 237
Subspace, norming 93 134 193 197 276
Subspace, proper 13
Subspace, quasicomplemented 377 379
Superdifferential 320
Support supp(f) 114 328
Support supp(x) 5
System, biorthogonal 139
Theorem, 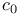 complementation 142 143 complementation 142 143
Theorem,  lifting 141 lifting 141
Theorem, 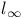 injective 142 injective 142
Theorem, Alaoglu 71 118
Theorem, almost block subspace 173
Theorem, approximation 329
Theorem, Auerbach 139
Theorem, Banach contraction 227
Theorem, Banach — Dieudonne 125
Theorem, Banach — Mazur 144
Theorem, Banach — Steinhaus 68 69
Theorem, Banach — Stone 79
Theorem, basic sequence 169 170 181
Theorem, Bessaga — Pelczynski 173 186
Theorem, bipolar 119
Theorem, Bishop — Phelps 83
Theorem, Brouwer 229
Theorem, Caratheodory 121
Theorem, Cauchy — Schwarz 3 16
Theorem, Choquet lemma 77
| Theorem, Choquet representation 123
Theorem, closed graph 51 57
Theorem, DFJP 366 371
Theorem, dual representation 44 45 47 4
Theorem, Dvoretzky 291
Theorem, Dvoretzky — Rogers 373
Theorem, Eberlein — Smulian 85 128 130
Theorem, extension 40 188 273
Theorem, Fredholm alternative 209
Theorem, Gelfand 213
Theorem, Goldstine 73
Theorem, Gorelik principle 353
Theorem, Hahn — Banach 37 40
Theorem, Helly 33 92
Theorem, Hilbert space is 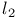 20 20
Theorem, Holder inequality 3
Theorem, invariant subspaces 230
Theorem, James 84 168 185
Theorem, Josefson — Nissenzweig 88
Theorem, Kadec 244 248 250 301
Theorem, Kaplansky 129
Theorem, Khintchine 177
Theorem, Korovkin 240
Theorem, Krein 85
Theorem, Krein — Milman 76 101
Theorem, local reflexivity 291 292
Theorem, Mackey et al. 120
Theorem, Markov — Kakutani 228 238
Theorem, Mazur 70 118 422
Theorem, Milman 78
Theorem, Minkowski inequality 4
Theorem, norm attained 40 83 262
Theorem, open mapping 50 57
Theorem, perturbation of basis 171
Theorem, Pietsch factorization 374
Theorem, Pitt 175
Theorem, Ramsey 423
Theorem, Riesz lemma 13
Theorem, root lemma 423
Theorem, Schauder 207 229 230
Theorem, Schur 146
Theorem, selection principle 173
Theorem, separable reduction 254
Theorem, separable spaces in  140 140
Theorem, separable spaces in 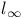 142 142
Theorem, separable spaces in C[0,1] 144
Theorem, separation 41 43 69 70 80 117 330
Theorem, Simons's inequality 80
Theorem, Smulian lemma 243
Theorem, Sobczyk 142
Theorem, spectral decomposition 223 226
Theorem, subspaces of 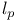 174 174
Theorem, uniform boundedness 68 69
Theorem, variational principle 83 317 326 327
Topology, 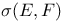 117 117
Topology, locally convex 108
Topology, Mackey 120 121
Topology, metrizable 71 110 135 417
Topology, norm 66 121
Topology, weak  64 96 129 391 64 96 129 391
Topology, weak star  64 71 64 71
TREE 199 294 295 308 309
Unit ball  2 2
Unit sphere 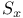 2 2
Variational Principle 83 317 326 327
Vector, cyclic 237
Vector, fixed point 227
Vector, orthogonal 17 225 276
Vector, standard unit 164
Weight w(T) 424
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![${W}_{p}^{k}[0,1]$](/math_tex/d454920100c3a3ea59de1daef2758c3e82.gif)
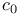 complementation
complementation  lifting
lifting  injective
injective