Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Fienberg S., Holland P.W., Bishop Y.M. — Discrete Multivariate Analysis
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Discrete Multivariate AnalysisÀâòîðû: Fienberg S., Holland P.W., Bishop Y.M.Àííîòàöèÿ: The scientist searching for structure in large systems of data finds inspiration in his own discipline, support from modern computing, and guidance from statistical models. Because large sets of data are likely to be complicated, and because so many approaches suggest themselves, a codification of techniques of analysis, regarded as attractive paths rather than as straitjackets, offers the scientist valuable directions to try. The literature on discrete multivariate analysis, although extensive, is widely scattered. This book brings that literature together in an organized way.
ßçûê: Ðóáðèêà: Ìàòåìàòèêà /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Ãîä èçäàíèÿ: 2007Êîëè÷åñòâî ñòðàíèö: 568Äîáàâëåíà â êàòàëîã: 14.04.2008Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
see “Freeman — Tukey” see “Likelihood ratio statistic see “Stochastic order” “Stochastic see “Pearson's chi square” Additive models 23—24; see also “Partitioning chi square” “Lancaster's Agreement, measures of 393—400 501—502; measures AID see “Automatic interaction detection” Angular transformation for binomial 367—369 491—492; “transformations variance-stabilizing” Anomalies in data 332—337 Arcsin transformation 367—369 491—492 Association, measures of, asymptotic variances for 374 501—502 Association, measures of, for 376—385 Association, measures of, for 385—393 Association, measures of, geometry of 383—385 Association, measures of, interpretability of 374—375 Association, measures of, norming 375—376 Association, measures of, sensitivity to margins 375 392—393; measures “Correlation “u-terms” Association, measures of, symmetry 376 Association, surface of constant 52—53 Asymptotic theory 457—530; see also “Bayes estimators” Automatic interaction detection 360 BAN (best asymptotic normal) 58 26 349 352 518 Bayes estimators 404—410 Bayes estimators, asymptotic results for 410—416 Bayes estimators, risk function of 406—407 Bayes estimators, small sample results for 416—419 421—424 Binomial distribution see also “Sampling distributions” Binomial distribution, angular transformation for 332—337 367—369 491—492 Binomial distribution, asymptotic distribution of powers 478—479 488 Binomial distribution, asymptotic normality of 464—465 Binomial distribution, behavior of minimax estimators for 416—417 Binomial distribution, estimation of proportion 437 Binomial distribution, estimation of sample size 437—438 Binomial distribution, moments of 436—437 Binomial distribution, negative 316—317 339—340 452—454 500 Binomial distribution, orders of 477 Binomial distribution, variance of squared proportions 485 Binomial distribution, variance stabilization for 491—492 Birch's results for MLEs, regularity conditions for 509—5 Birch's results for MLEs, uniqueness of 69 Block-diagonal table, l8 2 Block-stairway table, l9 4 98 Block-triangular table l9 4 98 Bootstrap-Bayes estimators see “Pseudo-Bayes estimators” Breaking-apart see “Rearranging data” BSS (between-group sum of squares) 390 Capture-recapture models, general 246—254 Capture-recapture models, incomplete tables and 233 237—239 246—247 Capture-recapture models, interpreting dependencies in 230 255 Capture-recapture models, three-sample 237—245 Capture-recapture models, two-sample 231—237 Cell values see also “Configuration” “Zero Cell values, elementary 13 61 Cell values, nonelementary 61 Cell values, smoothing 123 401—433 Cell values, standardized residual 136—139 Cell values, sums of 61 Chains, Markov for different strata 277—279 Chains, Markov, order of 269—270 Chernoff — Pratt theory see “Stochastic order” “Stochastic Chi square distribution, percentage points of 527; see also “Chi square statistic” Chi square statistic see also “Minimum logit “Neyman's “Pearson's Chi square statistic, association measures based on 330—332 385—387 Chi square statistic, asymptotic distribution, under alternative hypothesis 329—330 473—474 518 Chi square statistic, asymptotic distribution, under null hypothesis 472—473 516—218 Chi square statistic, comparing several 330—332 Closed-form estimates see “Direct estimates” Cochran's Q test 307—309 Cochran's test for combined tables 146—147 Cohen's measure of agreement, K 395—397 Collapsing, general definition of 47 Collapsing, general theorem for 47—48 Collapsing, illustration of 41—43 Collapsing, theorem for 3 Collapsing, two-way tables 27—28 Collapsing, way array 39—40 Combination of 365—366; see also “Mantel — Haensel test” “Collapsing” Combining categories 27—29; see also “Collapsing” Complete data, fitting incomplete models to 111—114; see also “Incomplete arrays” “Comprehensive Complete tables, definition of 58 Comprehensive model, definition 38 66—67 Computer programs 7 Conditional distribution see also “Incomplete tables” Conditional distribution, exact theory for 364—366 Conditional distribution, for Poisson variates 440—441; Conditional tests for interaction 148 364—366 Conditional tests for marginal homogeneity 293—296 307—309 Confidence interval see also “Variance asymptotic” Confidence interval for measures of association 374 380 382 Confidence interval, asymptotic for cell probability, p 478 Confidence interval, use of asymptotic variances for 499—500 Configuration of same order, degrees of freedom 119—122 Configuration, correspondence of, with u-terms 66 Configuration, definition of 61 Configuration, empty cells in 90 Connectivity see “Separability” Constructing tables 25—26 Contingency tables 57 Continuous variables 360 Contrasts see “Linear contrasts” Convergence in distribution 463—465 467—475 Convergence in distribution and 478—479 Convergence in distribution and 474 Convergence in distribution and probability 477—479 Convergence in probability 465—467 Convergence of moments 484—486 Correlation coefficient, association measures based on 380—385 Correlation coefficient, chi square and 382 Correlation coefficient, partial, related to collapsing 41 Correlation coefficient, related to cross product 14—15 Correlation coefficient, variance stabilization of 500—50 Cramer's measure of association, V 386—387 Cross-product ratio as loglinear contrast 15 26—27 Cross-product ratio related to correlation coefficient 15 Cross-product ratio related to u-terms 17—18 Cross-product ratio, association measures based on 377—380 393 Cross-product ratio, asymptotic variance of 377 494—497 Cross-product ratio, definition of 13 Cross-product ratio, functions of 379 601 Cross-product ratio, interpretation of 14—15 Cross-product ratio, properties of 14 377 Cross-validation of models 319—320 Cyclic descent, method of see “Fitting iterative proportional” D-association see “Separability” D-separability see “Separability” Degrees of freedom for closed-form models 121—122 Degrees of freedom for complete tables 25 35 66 114—122 Degrees of freedom for marginal homogeneity 287 294 307 Degrees of freedom for quasi-independence 187—188 Degrees of freedom for quasi-loglinear models 216—220 Degrees of freedom for quasi-symmetry 287 303 Degrees of freedom for symmetry 283 301—302 Degrees of freedom, adjusting, for empty cells 115—119 Delta method for binomial distribution 481—482 Delta method for calculating asymptotic distributions 486—502 Delta method for capture-recapture problem 249—250 Delta method, multivariate theorem 492—497 Delta method, one-dimensional theorem 487—490 Deming — Stephan procedure see “Fitting iterative Direct estimates for multiway incomplete tables 217 221—223 248 Direct estimates for quasi-independence 192—201 Direct estimates in three or four dimensions 74—75 Direct estimates, difference between models with 129—130 Direct estimates, equivalence to iterative 74 201—202 Direct estimates, partitioning 170—171 Direct estimates, rules for detecting 76—77 Direct estimates, theorems for detecting 78—82 Dirichlet distribution 405—406 Disagreement 398—399; see also “Agreement” Distributions see Sampling distributions e, approximating 460—462 Empirical-Bayes see “Pseudo-Bayes” Empty cells see “Zero entries” Entropy, maximum, theorem relating to linear models 346; see also “Information theory” Error, prediction, measures of reduction in 387—389 Estimability of parameters in incomplete table 219—220 Estimability, compared with connectedness 2l5 Estimation see “BAN” “Bayes “Information “Maximum “Minimum methods” “Minimum Exact theory for 364—365 Exact theory for combined tables 365—366 Exact theory, practicability of 366 Exponential distribution as limit of long waiting times 467—468 Exponential distribution, distribution of minimum 477—478 Fitting, iterative proportional see also “Maximum likelihood estimates” Fitting, iterative proportional for asymptotic variances 250—251 253—254 Fitting, iterative proportional for MLEs 83 Fitting, iterative proportional for quasi-symmetry 289 Fitting, iterative proportional in three dimensions 84—85 Fitting, iterative proportional, classical usage 97—102 337 392 Fitting, iterative proportional, convergence of 85—87 94—95 289 Fitting, iterative proportional, general algorithm 91—97 Fitting, iterative proportional, incomplete tables 188—192 217 Fitting, iterative proportional, initial estimates 92—95 Fitting, iterative proportional, properties of 83 Fitting, iterative proportional, stopping rules 95—96 Four-fold table ( 11—12 Four-fold table ( 13—14 Four-fold table ( 49—55 383—385 Freeman — Tukey, chi square 130 137 513—516 Freeman — Tukey, transformation for binomial 367—368 492 Freeman — Tukey, transformation for Poisson 137 492 Freeman — Tukey, transformation, residuals for 130 137—140 334—337 Frequency of frequencies 337—342; see also “Sampling distributions” Geometry of Bayes estimators 408—410 Geometry of measures for 49—55 383—385 Gini's definition of variation 389—390 Goodness-of-fit see also “Chi square” “Likelihood “Neyman's “Pearson's Goodness-of-fit for sampling distributions 3l5—317 Goodness-of-fit of internal cells l36—141 Goodness-of-fit when model is false 329—332 Goodness-of-fit, asymptotic distribution of test statistics for 513—529 Goodness-of-fit, asymptotic equivalence of 3 statistics 513—514 Goodness-of-fit, fitting and testing for 317—324 Goodness-of-fit, multinomial general theory of 507—508 Goodness-of-fit, too good a fit 324—329 Hansen frequencies, asymptotic distribution of 489 Hierarchy of models 320—324 Hierarchy principle 33 38 67—68 Homeogeneity of proportions 347 Homeogeneity, marginal 54—55 282 Homeogeneity, test for 293—296 306—309 Homogeneous Markov chain 262 Hypergeometric distribution see also “Exact theory” Hypergeometric distribution, multivariate 450—452 Hypergeometric distribution, univariate 488—450 Incomplete arrays for subsets of complete arrays 111 206—210 225—228 Incomplete arrays, multiway 210—225 Incomplete arrays, square tables and 283 290 Incomplete arrays, triangular 31 Incomplete arrays, two-way 178—206 Independence as lack of association 374—380 Independence in rectangular array 28—29 Independence in three-way array 38 Independence, quasi 178—182 287—293 Independence, surface of 51 Indirect estimates see “Fitting iterative “Partitioning Information theory, minimum discrimination information (MDI) 344—347 Information theory, model generation 345—346 Information theory, modified MDI (MMDI) 295—296 347 Interaction see also “u-terms” Interaction, assessing magnitude of 146—155 Interaction, test for 146—155 364—366 Irregular arrays 31 48; Isolates l93 Iterative proportional fitting 83—102 188—191 Iterative scaling see “Iterative proportional fitting” Jackknifing 3l9 K, sum of Dirichlet parameters 401—402 405—408 420—426; K” Kullback — Liebler distance 345; see also “Information theory” “Likelihood Lambda as measure of association 388—389 Lambda as weight for Dirichlet prior 405—406 419—426 429—433 Latent structure analysis 344 Least squares, weighted 352—357 Likelihood ratio statistic, 125—130 Likelihood ratio statistic, 129—130 158—160 Likelihood ratio statistic, 191 Likelihood ratio statistic, 160—161 Likelihood ratio statistic, 283 Likelihood ratio statistic, 513—5 6 Likelihood ratio statistic, 169—175 Likelihood ratio statistic, 125—126 Likelihood ratio statistic, 120 127 Likelihood ratio statistic, 293—294 307 Likelihood ratio statistic, 58 Likelihood ratio statistic, 127—130 Linear contrast see also “Log-linear model” “u-terms” Linear contrast, asymptotic variance of 494—497 Linear contrast, interpretations of 15 16 26—27 181 211—222 Linear models see “Additive models” Log-linear model see also “Linear contrast” “Cross “Direct Log-linear model for 32—33 Log-linear model for 16—17 79 Log-linear model for 35—41 Log-linear model for 37 39 Log-linear model for 24—26 179 Log-linear model with terms of uniform order 119—121 156—158 Log-linear model, general 42—47 Log-linear model, general, interpretation of 45—47 Log-linear model, random effects models 371 Logistic response function see also “Logit model” Logistic response function, multivariate 360 Logistic response function, univariate 357—360 Logit model for 30 Logit model, alternatives to 367—371 Logit model, continuous variable 358 Logit model, definition of 22—23 Logit model, discrete variable 357 361 Logit model, minimum c-hi square for 355—357 Logit model, mixed variable 358 Loglinear contrasts see “Linear contrast” Loops, closed 76 Mantel — Haenszel test 133 147—148 151 Marginal homogeneity see “Homogeneity” margins see “Cell values” “Configuration” Margins, lines of constant 53 Margins, measures insensitive to 392—393 Markov models for cross classified states 273—279 Markov models for different strata 277—279 Markov models, assessing order of 269—270 Markov models, assessing order of, for aggregate data 260 261 Markov models, higher order 267—270 Markov models, single sequence transitions of 270 273 Markov models, time-homogeneity 261—267 269 Maximum entropy 345—346; see also “Information theory” Maximum likelihood estimates (MLEs) see also “Fitting Iterative proportional” “Birch's “Direct Maximum likelihood estimates (MLEs) for marginal homogeneity 294—295 306 Maximum likelihood estimates (MLEs) for Markov chain transition probabilities Maximum likelihood estimates (MLEs) 262—263 267—268 Maximum likelihood estimates (MLEs) for quasi-symmetry 289 306—319 Maximum likelihood estimates (MLEs) for symmetry 28 330—302 Maximum likelihood estimates (MLEs), advantages of 58 Maximum likelihood estimates (MLEs), asymptotic behavior of 509 513 Maximum likelihood estimates (MLEs), conditional for closed populations 231 238 Maximum likelihood estimates (MLEs), existence of, for incomplete tables 186 216 Maximum likelihood estimates (MLEs), expansion of, for multinorniat 511—513 Maximum likelihood estimates (MLEs), methods of obtaining 71 83 Maximum likelihood estimates (MLEs), relative precision of 313—315 Maximum likelihood estimates (MLEs), suitability for likelihood ratio statistic 125—126 Maximum likelihood estimates (MLEs), uniqueness of in incomplete tables 185 Maximum likelihood estimates (MLEs), when model is incorrect 513 McNemar test 258 285
Ðåêëàìà
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



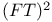

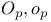 notation
notation 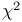
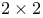 tables
tables 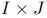 tables
tables 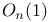
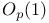
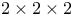 table
table 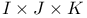 table
table 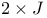 table
table