Àâòîðèçàöèÿ
Ïîèñê ïî óêàçàòåëÿì
Fienberg S., Holland P.W., Bishop Y.M. — Discrete Multivariate Analysis
Îáñóäèòå êíèãó íà íàó÷íîì ôîðóìå Íàøëè îïå÷àòêó?
Íàçâàíèå: Discrete Multivariate AnalysisÀâòîðû: Fienberg S., Holland P.W., Bishop Y.M.Àííîòàöèÿ: The scientist searching for structure in large systems of data finds inspiration in his own discipline, support from modern computing, and guidance from statistical models. Because large sets of data are likely to be complicated, and because so many approaches suggest themselves, a codification of techniques of analysis, regarded as attractive paths rather than as straitjackets, offers the scientist valuable directions to try. The literature on discrete multivariate analysis, although extensive, is widely scattered. This book brings that literature together in an organized way.
ßçûê: Ðóáðèêà: Ìàòåìàòèêà /Ñòàòóñ ïðåäìåòíîãî óêàçàòåëÿ: Ãîòîâ óêàçàòåëü ñ íîìåðàìè ñòðàíèö ed2k: ed2k stats Ãîä èçäàíèÿ: 2007Êîëè÷åñòâî ñòðàíèö: 568Äîáàâëåíà â êàòàëîã: 14.04.2008Îïåðàöèè: Ïîëîæèòü íà ïîëêó |
Ñêîïèðîâàòü ññûëêó äëÿ ôîðóìà | Ñêîïèðîâàòü ID
Ïðåäìåòíûé óêàçàòåëü
MDI see “Information theory” mgf see “Moment generating function” Minimax estimates 407 Minimum distance measure see also “Pearson's chi square” “Neyman's “Minimum Minimum distance measure, asymptotic variance of 518—519 Minimum distance measure, methods 504—505 Minimum logit 355—357 MLE see “Maximum likelihood estimates” MMDI see “Information theory” Model see also “Log-linear model” “Additive Model, selection of 155 168 Model, simplicity in building a 312—313 Moment generating function, to show convergence 469; see also “Sampling distribution” Moments see “Binomial distribution moments “Hypergeometric “Multinomial “Poisson Moments, limits of 485 Moments, methods of 505 507 Moments, order of 485 486 Multinomial distribution, asymptotic normality of 469—472 Multinomial distribution, asymptotic variance of loglinear contrasts for 494—497 Multinomial distribution, estimation for 504—505 Multinomial distribution, formal stochastic structure for 480—481 Multinomial distribution, general theory for estimating and testing with a 502—508 Multinomial distribution, goodness-of-fit tests 507—508 Multinomial distribution, negative multinomial 454—456 Multinomial distribution, product multinomial 63 70—71 Multinomial distribution, sampling distribution 63 441—446 Multinomial distribution, variance of log-linear contrasts 494—497 Multiplicative models 225—228 320—324; Multivariate normal distribution, asymptotic distribution for multinomial 469—472 Multivariate normal distribution, estimating the mean of 403 Nested models see also “Likelihood ratio statistic Nested models, difference in 524—526 Neyman's chi square, minimizing 349—350 Neyman's chi square, with linear constraints 351—352 Neyman's chi square, with linear constraints, equivalence to weighted least squares 352—354 Noninteractive cell 181—182 193—194 Normal approximations to the binomial 464—465 Norming measures of association 375—376 Notation for models, dimension-free 61—62; see also “O notation” O,o notation, Chernoff — Pratt 479—480 481 O,o notation, conventions in use of 459—460 O,o notation, definitions 458—459 460 O,o notation, generalized for stochastic sequences 475—484 O,o notation, related to order of moments 485—486 Occurrence in probability 482—484 Outliers 140—141 P see “Pearson's measures of association” Panel studies 257—260 265—267 Parameters see “u-terms” Partial association models, degrees of freedom for 121—122 Partial association models, fitting 161—165 Partitioning chi square 524—526 Partitioning chi square, calculus of Goodman 169—175 Partitioning chi square, Lancaster's method 361—364 Partitioning chi square, likelihood ratio statistic 524—526 Pdf (probability density function) 63 Pearson's chi square see also “Chi square distribution” Pearson's chi square, asymptotic distribution of 472—474 Pearson's chi square, asymptotic relation to other statistics 513—516 Pearson's chi square, compared with 124—125 Pearson's chi square, correction for continuity 124 258 Pearson's chi square, definition of 57 Pearson's chi square, incomplete tables 191 Pearson's chi square, large samples and 329—332 Pearson's chi square, limiting distribution of under alternative 329—332 518 Pearson's chi square, limiting distribution of under null model 516—518 Pearson's chi square, limiting distribution of, for complex cases 520—522 Pearson's chi square, minimizing 348—349 Pearson's chi square, noncentral distribution 473—474 518 Pearson's measures of association, 330 385—387 Pearson's measures of association, P 382—383 385—387 Percentage points, for 527—529 Poisson distribution see also “Frequency of frequencies” “Hansen “Maximum “Sampling Poisson distribution, asymptotic distribution of powers of mean 489—490 Poisson distribution, relationship to multinomial 440—441 446—448 Poisson distribution, sampling distribution 62 185—186 438—441 446—448 Poisson distribution, truncated variates 503—504 506 607 521—522 523—524 Poisson distribution, variance-stabilizing transform for 492 Population-size estimation 229—256 Pratt, occurrence in probability 482—484; see also “Stochastic sequence” “Notation dimension-free” PRE (proportional reduction in error) 387—389 PRECISION 313—315; see also “Variance” Probit transformation 367 Propagation of errors see “Delta method” Pseudo-Bayes estimators 408—410 419—423 Pseudo-Bayes estimators, asymptotic results for 410—416 Pseudo-Bayes estimators, small sample results for 416—419 PV (predictive value) 21—22 q see “Association measures “Cochran's “Yule's Quasi-independence see “Independence” Quasi-loglinear 210—212 Quasi-perfect mobility 206—208 Quasi-symmetry see “Symmetry” R 381—385 Rates, adjusting for multiple variables 123 133—136 Rates, direct standardization 131—132 Rates, generic form 133—136 Rates, indirect standardization 132 Rates, standard mortality ratio 132 135 Rearranging data, breaking apart an 207—209 Rearranging data, fitting by stages 107—108 Rearranging data, in 15—16 Rearranging data, partitioning 105—107 Rearranging data, relabeling 102—105 Regularity conditions see “Birch's results for MLEs” Relatives, high order 34 Risk see also “Cross-product ratio” Risk for comparing Bayesian estimators 406—408 Risk, expected squared error 313—335 Risk, ratios, limiting 414—416 Risk, relative 15 Sampling design, constraints on models 36 Sampling design, stratified 29—30 Sampling distribution 62—64 185 212; “Hypergeometric “Multinomial “Poisson Sampling distribution, effect on model selection 70—71 Sampling models, search for 315—317 Saturated models 9 Scoring categorical variables 360 Search procedures see “Stepwise model selection” Sensitivity 20—21 48 Separability in many dimensions 212—216 Separability, dealing with 184—187 Separability, in 182—183 Separability, semi- 194 Simplicity in model building 312—315 Smoothed counts see “Cell values smoothing” SMR (Standard Mortality Ratio) see “Rates standard Sparse multinomials 410—413 Specificity 20—22 48 Square tables 281—309 320—324 339—342 347 Standard deviation and stochastic order 476—477 Standardization see “Fitting iterative classical “Rates” Stationarity, of transition probabilities 261—267 269 Stepwise model selection 165—167 Stochastic order see also “Stochastic sequence” Stochastic order of exponential variables 477—478 Stochastic order, Chernoff — Pratt theory for 479—484 Stochastic order, definition of 475—476 Stochastic order, methods for determining 476—477 Stochastic orders of moments 485—486 Stochastic sequence see also “Stochastic order” Stochastic sequence, Chernoff — Pratt theory for 479—480 Stochastic sequence, convergence of 463—475 Stochastic sequence, determining order of 476—478 Stochastic sequence, formal structure of 480—482 Structural models, definition of 9—10 Structural models, uses of 11 Sufficient statistics 64—67 Sufficient statistics for three-dimensional models 66 Sufficient statistics, general derivation of 68—69 Sufficient statistics, minimal set of 66 Sufficient statistics, minimal set of, and direct estimates 78 Summary statistics see “Association measures of” “Chi “Frequency of “Rates” ”Sufficient Suppressing parameters 332—337 Symmetry in association measures 376 Symmetry in square tables 258 282—286 299—306 347—348 Symmetry, exact 260 Symmetry, quasi- 286—292 303 296 Symmetry, relative 260 Synergism see “Worcester model” t see “Tsehuprow's measure of association” Taylor expansion 460—461 Testing see also “Interaction” “Partitioning Testing and fitting 317—324 Testing, simplifying structure before 150 Testing, use of asymptotic variances for 498—499 Tetrahedron, of reference 50 Transformations, variance-stabilizing 366—371 491—492; “Arcsine “Logit “Freeman “Probit Transition probabilities 262—269 Transition probabilities, single sequence 270—273 tree structures 360 triangular arrays see “Incomplete arrays” Trinomial distribution, for risk of pseudo-Bayesian estimators 417—419 Tschuprow's measure of association, T 385—387 TSS (total sum of squares) 390 U as collection of u-terms 62 U as measure of association 389—392 u-terms see also “Log-linear model” “Linear u-terms, definition 17 18 u-terms, generalized notation 61—62 u-terms, interpretation of 29—30 32—34 u-terms, relationship to cross-product ratios 17—18 u-terms, standardized estimates of 141 146 156 u-terms, variance of 494—497 Unsaturated models 9 V, Cramer's measure of association 386—387 Variance see also “Delta method” Variance for capture-recapture problem 233 240—242 248—254 Variance for distance measures 518—519 Variance, asymptotic 498—499 Variance, asymptotic for confidence intervals 499—500 Variance, asymptotic for hypothesis testing 488—499 Variance, methods for computing 248—251 Variance, stabilizing transformations 491—492 500—501 Variation, measures of 389—393 Waiting times 467—468 Worcester model 111 WSS (within-group sum of squares) 390 Y see “Association” “Yule” Yule's Q as measure of association 378—380 501 Yule's Y as measure of colligation 378—380 Zero entries see also “Configuration” Zero entries, deviations in cells with 140 Zero entries, diagonals with, in square tables 296—299 Zero entries, invalidating model 72 Zero entries, random, defined 59 177 Zero entries, structural 31 59 93 177 Zero entries, unrepeated events in Markov chains 275—276
Ðåêëàìà
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



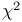

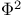
 distribution
distribution  measuring association
measuring association 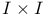 table
table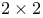 table
table 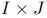 tables
tables