|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Frazer R.A., Duncan W.J., Collar A.R. Ч Elementary Matrices |
|
|
 |
| ѕредметный указатель |
Equation, detei-minantal see УDeterminantal equationФ
Equation, indicial 215
Equation, semi-period, for steadv frictional oscillations 346 348Ч350 364 370 393
Equations, dynamical, for frictional systems 335Ч345
Equations, geometrical, of a dynamical system 262 277
Equations, Hamilton's dynamical 274Ч276 289
Equations, Lagrange's dynamical 164 194 195 197 269Ч272 277Ч279 289
Equations, linear algebraic 27 98Ч97 125Ч133
Equations, linear difference 73 148
Equations, linear dyoamical see УLinear dynamical equationsФ
Equations, linear ordinary differential see УLinear ordinary differential equationsФ
Equations, linear partial differential 60Ч52 227
Equations, terminal 342
Equilibrium, conditions for 262Ч265
Equilibrium, conservative system disturbed from 281
Equivalent, latabda-matrices 90Ч92
Equivalent, matrices 89
Equivalent, systems of differential equations 158 159 161
Euler, L. 250
Existence theorems 212Ч214
Exponential function of square matrix, applied in method of mean coefficients 232
Exponential function of square matrix, defined 41Ч43
Exponential function of square matrix, differentiation of 45Ч46
Exponential function of square matrix, solution of differential equations by 209Ч211 221 333
Factors, invariant 91Ч92
Factors, linear 92
Fields of force, conservative and non-conservative 263Ч265
Finite rotations, matrices representing 118Ч249 251Ч254
Flexibilities 265
Flexibility matrix, defined 265
Flexibility matrix, used to calculate dynamical matrix 309
Flexural oscillations of tapered beam 318Ч320
Flexure-torsion oscillations of aeroplane wing 266 30£~307.
Fluid flow across annulus 229Ч230
Flutter, critical speed for 291 302 307 358 359 389
Flutter, experimental observations of 332 333 395
Flutter, influence of solid friction on 360 362
Flutter, practical meaning of 359
Flutter, simple theory of 358
Forced motion of deviation 280
Forced oscillations, of aerodynamical systems 802Ч307
Forced oscillations, resonant 183 305
Forces, conservative 263Ч265
Forces, generalised 263Ч265 270 277
Forms, bilinear and quadratic 28Ч30
Fractional powers of matrices 38 81 82
Frame of reference, angular coordinates of a three-dimensional 250 255 256
Frame of reference, angular momenta referred to a moving 257
Frame of reference, angular velocities of a moving 248 253 255
Frame of reference, defined 246
Frame of reference, kinetic energy referred to a moving 267
Frame of reference, Lagrange's equations with a moving 277Ч279
Frame of reference, moving, in two dimensions 247Ч248
Frame of reference, velocities and accelerations referred to a moving 248 256
Frazer, R.A. 15, 21, 23, SO 36 88 39 40 42
Free, disturbed steady motion of an aeroplane 284Ч287
Free, motion of deviation 280
Freedom, degrees of 259 261 273
Frequencies, calculated by iterative methods 308Ч331
Frequencies, calculated by Rayleigh's principle 300 310 316
Frequencies, conservative system with equal 198Ч200 292Ч295 309 310 322Ч325
Frequency, diagram, for tail oscillations 359 361
Frequency, parameter, for aerofoil oscillations 385
Friction, solid see УSolid frictionФ
Frobenius, F.G. 215
Frobenius, method of 216
Fundamental solutions of linear differential equations 214Ч215 219 220 223 224
Fuselage, oscillations involving torsion of 359Ч381
Galerkin, method of 224Ч231
Galerkin, V.G. 224 226 227 228 229 230 231
Generalised, aerodynamical derivatives 284
Generalised, coordinates, transformation of 282
Generalised, coordinates, velocities, and accelerations 260Ч262
Generalised, forces 263Ч265 270 277
Generalised, momenta 274Ч276
Generalised, moments and products of inertia 281 284
Geometric constraints 259Ч260 261 270
Geometrical equations, for a dynamical system 262 277
Graphical treatment, of binary frictional systems 354Ч367 372Ч380
Graphical treatment, of conditions for steady oscillations 387Ч389
Grossman, E.P. 26
Gyrostatic coefficients 278 279 283
Hamilton, Sir W.R. 70 274 275
Hamiltonian, equations of motion 274Ч276 289
Hamiltonian, function 275
Heaviside, identity of, expressed by matrices 176
Heaviside, method of 197 203Ч204
Heaviside, O. 176 197 202 203
Hermitian matrix 33 155
Hertz, H. 260
High powers of a matrix 80 133Ч145
Holonomous, or holonomic, systems, defined 260
Holonomous, or holonomic, systems, generalised coordinates of 261
Holonomous, or holonomic, systems, Hamilton's equations for 274Ч276
Holonomous, or holonomic, systems, Lagrange's equations for 269Ч272 277Ч279
Homogeneous, strain 258
Homogeneous, system of differential equations 157
Hooke, R. 266
Idempotent matrices 79
Ignorable coordinates, denned 272
Ignorable coordinates, disturbed steady motion of systems with 282Ч283
Ignorable coordinates, dynamical equations for systems with 272Ч274
Independent variables, change of 48Ч51
Index law for matrices 37Ч38
Indicial equation 215
Inertia, force 269
Inertia, generalised moments and products of 281 284
Inertia, matrix 284 288
Inertia, principal axes of 257Ч258
Infinite series of matrices 40Ч41 53 81
Influence numbers 265
Inge, E. L. 5
Integration of matrices 52Ч56
Interpolation formula, Lagrange's 40
Invariant factors 91Ч92
Inverse matrices see УReciprocal ReciprocationФ
Irregular singularity 215
Isolation, method of 197
Iterative methods, for coefficients in Sylvester's expansion 138Ч141
Iterative methods, for construction of characteristic equation 142
Iterative methods, for frequencies 308Ч331
Iterative methods, for latent roots 134Ч138 140Ч145 148Ч151
Iterative methods, for linear algebraic equations 132Ч133
Iterative methods, for linear dynamical problems 308Ч331
Iterative methods, general remarks on 150Ч151 309Ч310
Iterative methods, modal columns calculated by 141Ч145 * 151 308Ч310
Iterative methods, overtones calculated by 309 312Ч314 325 330r>331
Iterative methods, twist of aeroplane wing calculated by 325Ч327
Jacobians, relations between 49
Jeans, Sir J.H. 333
Jeffreys, H. 16
Jones, W.P. 23 36
Kelt, and, P. 3
Kinematic constraints 259Ч260 261 270
Kinetic energy, discriminants of 272 337 370
Kinetic energy, expressed by generalised coordinates and velocities 270 282
Kinetic energy, expressed by generalised momenta and velocities 275
Kinetic energy, expressed by submatrices 272 282
Kinetic energy, expressed for moving axes 257
Kinetic potential 271
Kinosthenic coordinates see УIgnorable coordinatesФ
Kubo, S. 35
Kussner, H.G. 33
Lagrange's equations, constructed 269Ч271
Lagrange's equations, expanded form of 271Ч272 281
Lagrange's equations, for systems referred to moving axes 277Ч279
Lagrange's equations, linear, direct solution of 194 195
Lagrange's equations, linear, expressed as first-order system 164 289 327
Lagrange's equations, linear, special solution of 197 198Ч200
Lagrange's equations, modified for ignorable coordinates 272Ч274 282Ч283
| Lagrange's interpolation formula 40
Lagrange, J.L. 40 269
Lagrangian function, defined 271
Lagrangian function, modified, for ignorable coordinates 272Ч274 282
Lamb, Sir H. 29
Lambda-determinant 157
Lambda-matrices, equivalent 90Ч92
Lambda-matrices, multiplication and division of 58Ч60
Lambda-matrices, Smith's canonical form for 91Ч92 181
Lambda-matrix, adjoint of 61Ч64 166Ч167
Lambda-matrix, defined 57 157
Lambda-matrix, degree of 67
Lambda-matrix, derived adjoints of 61 62 64 166
Lambda-matrix, determinantal equation of 61 see
Lambda-matrix, elementary divisors of 92
Lambda-matrix, invariant factors of 91Ч92
Lambda-matrix, leading matrix coefficient of 57
Lambda-matrix, linear factors of 92
Lambda-matrix, rank of 57 91 182
Lambda-matrix, reciprocal of 58
Lambda-matrix, remainder theorems for 59 60 70
Laplacian operator, transformation: of 51
Latent roots, calculated by iterative methods 134Ч138 140Ч145 148Ч151
Latent roots, classical submatrices containing 94
Latent roots, defined 64
Latent roots, diagonal matrix of 66
Latent roots, dominant 80 134Ч143 148 309
Latent roots, equal 65 67Ч71 75Ч77 83Ч87 93 135 137 138 140
Latent roots, non-dominant 143Ч145 331 see
Latent roots, of Hermitian matrix 155
Latent roots, of matrices connected by collineatory transformation 69
Latent roots, of polynomial of a square matrix 69
Latent roots, of symmetrical matrix 155
Latent roots, situation of 155
Leading matrix coefficient, of a lambdamatrix 57
Line matrix 2
Linear algebraic equations, expressed as matrix equation 8 18
Linear algebraic equations, solution of 27 96Ч97 125Ч133
Linear algebraic equations, solution of, by direct operation on rows 130Ч131
Linear algebraic equations, solution of, by iterative methods 132Ч133
Linear algebraic equations, solution of, by post-multiplication 126Ч130
Linear difference equation 73 148
Linear differential equations see УLinear ordinary differential equationsФ УLinear
Linear dynamical equations, confluent special solution of 198Ч200
Linear dynamical equations, direct solution of 191Ч192 194 195 295
Linear dynamical equations, for conservative system disturbed from equilibrium 281Ч282 291Ч300 308
Linear dynamical equations, for conservative system disturbed from steady motion 282Ч283
Linear dynamical equations, iterative solutions of 308Ч331
Linear dynamical equations, notation and terminology for 288Ч289
Linear dynamical equations, reduced to first-order Bystem 164 289 327
Linear dynamical equations, reducing variables for 195
Linear dynamical equations, special solution of 197
Linear dynamical equations, transformation of coordinates in 282
Linear factors 92
Linear ordinary differential equations with constant coefficients, "diagonal" systems of 160
Linear ordinary differential equations with constant coefficients, adjoint matrices for first-order system of 205
Linear ordinary differential equations with constant coefficients, boundary problems with 186
Linear ordinary differential equations with constant coefficients, change of order of boundary conditions for 190Ч191
Linear ordinary differential equations with constant coefficients, characteristic numbers for 187Ч188
Linear ordinary differential equations with constant coefficients, complementary function of 157 178Ч182
Linear ordinary differential equations with constant coefficients, confluent special solution of 198Ч200
Linear ordinary differential equations with constant coefficients, constituent solutions of 167Ч175
Linear ordinary differential equations with constant coefficients, conversion of, to first-order system 162Ч165 202
Linear ordinary differential equations with constant coefficients, direct solution of, for one-point boundary problem 191Ч195 207Ч209 295
Linear ordinary differential equations with constant coefficients, direct solution of, for two-point boundary problem 201
Linear ordinary differential equations with constant coefficients, equivalent systems of 158 159 181
Linear ordinary differential equations with constant coefficients, fundamental theorem for systems of 161
Linear ordinary differential equations with constant coefficients, general solution of simple first-order system of 206Ч207
Linear ordinary differential equations with constant coefficients, Heaviside's method for 203Ч204
Linear ordinary differential equations with constant coefficients, homogeneous and non-homogeneous systems of 157
Linear ordinary differential equations with constant coefficients, method of isolation for 197
Linear ordinary differential equations with constant coefficients, notation for one-point boundary problems with 188Ч189
Linear ordinary differential equations with constant coefficients, notation for systems of 156Ч157 178Ч180
Linear ordinary differential equations with constant coefficients, notation for two-point boundary problems with 200Ч201
Linear ordinary differential equations with constant coefficients, order of 156
Linear ordinary differential equations with constant coefficients, particular integral of 157 183Ч185 1G8 209
Linear ordinary differential equations with constant coefficients, simple first-order system of 202 209Ч211
Linear ordinary differential equations with constant coefficients, solution of, when 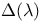 vanishes identically 181Ч182 vanishes identically 181Ч182
Linear ordinary differential equations with constant coefficients, special solution of general fiist-order system of 203Ч205
Linear ordinary differential equations with constant coefficients, special solution of simple first-order system of 207
Linear ordinary differential equations with constant coefficients, special solution of, for standard one-point boundary problems 195Ч200
Linear ordinary differential equations with constant coefficients, standard one-point boundary problems with 189 190
Linear ordinary differential equations with constant coefficients, transformation of dependent variables in 159Ч160
Linear ordinary differential equations with constant coefficients, triangular systems of 160Ч162
Linear ordinary differential equations with variable coefficients, characteristic numbers for 224 226Ч228 230Ч231
Linear ordinary differential equations with variable coefficients, continuation formula for systems of 219Ч222
Linear ordinary differential equations with variable coefficients, existence theorems for 212Ч214
Linear ordinary differential equations with variable coefficients, first-order systems of 213Ч214 216Ч218 220Ч224 232Ч233
Linear ordinary differential equations with variable coefficients, fundamental solutions of 214Ч215 219 220 223 224
Linear ordinary differential equations with variable coefficients, indicial equation for 215
Linear ordinary differential equations with variable coefficients, iregular singularities of 215
Linear ordinary differential equations with variable coefficients, notation for system of 215
Linear ordinary differential equations with variable coefficients, ordinary points of 212
Linear ordinary differential equations with variable coefficients, Peano Ч Baker method for first-order system of 217Ч218
Linear ordinary differential equations with variable coefficients, power series solution for first-order system of 222Ч224
Linear ordinary differential equations with variable coefficients, regular singularities of 215
Linear ordinary differential equations with variable coefficients, simple first-order system of 216 217Ч218 220Ч222 232Ч233
Linear ordinary differential equations with variable coefficients, singularities of 212Ч215 221
Linear ordinary differential equations with variable coefficients, solution of, by collocation and GaJerkin's method 224Ч231
Linear ordinary differential equations with variable coefficients, solution of, by mean coeficients 232Ч245
Linear ordinary differential equations with variable coefficients, solution of, by method of Frobenius 215
Linear ordinary differential equations with variable coefficients, system of, reduced to first order 215Ч217
Linear partial differential equations, change of variables in 50Ч52
Linear partial differential equations, methods of collocation and Galerkin for 227
Linear substitution 23Ч27 64
Linear transformation, denned 26
Linear transformation, matrix of 27
Linear transformation, triangular 31
Linear vector function 258
Loading, principal directions of 265Ч266
MacDuffee. C.C. 51
Mass balance of aeroplane control surfaces 302
Matrices, addition and subtraction of 4
Matrices, conformable 6 9 14 25
Matrices, conjugate 33
Matrices, continued products of 9Ч12 221
Matrices, differentiation of 43Ч52
Matrices, division of 22 58Ч60
Matrices, elementary operations on 87Ч89 90 96 97
Matrices, equal 4
Matrices, equivalent 89 90Ч92
Matrices, fractional powers of 38 81 82
Matrices, infinite series of 40Ч41 53 81
Matrices, integration of 52Ч56
Matrices, inverse 22 see ReciprocationФ
Matrices, multiplication of 6Ч12
Matrices, notation foi 1Ч3
Matrices, of differential operators 40Ч51 166
Matrices, partitioned 13Ч15
Matrices, permutabie 6 7 42 44
Matrices, predivision and postdivieion of 22
Matrices, products of 6Ч12
Matrices, reciprocal 22 see ReciprocationФ
Matrices, representing complex scalars and quaternions 35Ч36
Matrices, representing finite rotation 248Ч249 251Ч254
Matrices, Taylor's theorem for 44Ч45
Matrices, whioh commute 6 39 42
Matrices, with null product 23Ч24
Matrix, adjoint 21 see
Matrix, aerodynamical stiffness 284 285
Matrix, alternate 3 33
Matrix, characteristic 64
Matrix, column 2
Matrix, D- 157
Matrix, damping 284 288 386
Matrix, definition of 1
Matrix, degeneracy of a square 18 see
Matrix, derived 43Ч44
Matrix, determinant of a square 10
Matrix, diagonal 3 12Ч13 23 66 .89 91 93
|
|
 |
| –еклама |
 |
|
|
 |
 |
|
 |
|
ќ проекте
|
|
ќ проекте



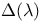 vanishes identically
vanishes identically