Авторизация
Поиск по указателям
Borwein J.M., Borwein P.B. — Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity
Обсудите книгу на научном форуме Нашли опечатку?
Название: Pi and the AGM: A Study in Analytic Number Theory and Computational ComplexityАвторы: Borwein J.M., Borwein P.B. Аннотация: Presents new research revealing the interplay between classical analysis and modern computation and complexity theory. Two intimately interwoven threads run though the text: the arithmetic-geometric mean (AGM) iteration of Gauss, Lagrange, and Legendre and the calculation of pi[l.c. Greek letter]. These two threads are carried in three directions. The first leads to 19th century analysis, in particular, the transformation theory of elliptic integrals, which necessitates a brief discussion of such topics as elliptic integrals and functions, theta functions, and modular functions. The second takes the reader into the domain of analytic complexity — Just how intrinsically difficult is it to calculate algebraic functions, elementary functions and constants, and the familiar functions of mathematical physics? The answers are surprising, for the familiar methods are often far from optimal. The third direction leads through applications and ancillary material — particularly the rich interconnections between the function theory and the number theory. Included are Rogers-Ramanujan identities, algebraic series for pi[l.c. Greek letter], results on sums of two and four squares, the transcendence of pi[l.c. Greek letter] and e[ital.], and a discussion of Madelung's constant, lattice sums, and elliptic invariants. Exercises.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1987Количество страниц: 414Добавлена в каталог: 11.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Generalized Legendre symbol 293 Generalized singular value function 185 Geometric series 91 Gini (38) 233 Gini's means 233 264 Glasser and Zucker (80) 68 290 293 303 Goldfield (85) 295 Gordon (61) 306 308 gosper 341 Gould and Mays (84) 263 Goursat (1881) 185 186 Gradshteyn and Ryzhik (80) 10 Grave 345 Graves-Morris 323 Greenhill (1892) 133 167 Gregory 339 348 381 Gregory's series 339 Guilloud 341 Halley's method 216 Hancock (09) 29 Hanna (28) 133 Hardy 80 187 Hardy (40) 141 314 Hardy and Wright 80 Hardy and Wright (60) 66 67 85 86 95 281 284 349 376 378 Hardy, Littlewood and Polya (59) 235 242 269 Height 371 hermite 135 264 348 359 Hermite and Stieltjes (05) 264 Heronian mean 237 269 270 Hexagonal lattice 292 Hexagonal sum 292 hilbert 348 353 354 Hilbert (1893) 348 Hirschhorn (85) 285 Holder's means 232 235 263 264 Holloway 188 Homogeneous mean 231 Homogeneous multidimensional mean 266 Horner's rule 204 Householder (70) 215 216 Hua (82) 294 349 375 Hughes (84) 175 Hurwitz zeta function 303 304 Hyberbolic arclemniscate 259 Hyberbolic function identities 74 75 100 Hypergeometric functions 332—334 Hypergeometric functions and series, Gaussian hypergeometric series 8 Hypergeometric functions and series, generalized 178 Hypergeometric functions and series, hypergeometric differential equation 11 Identric mean 234 Incomplete elliptic integrals 10 Incomplete elliptic integrals of first kind 10 58 60 Incomplete elliptic integrals of second kind 10 Incomplete elliptic integrals of third kind 10 Incomplete elliptic integrals, Eulers addition theorem 18 Inhomogeneous modular group, 113 117 Interpolation problem 204 Invariance principle 245 246 260 Invariants, evaluating 293 Irrationality measures 362 Irrationality measures for 371 Irrationality measures for 367 368 371 Irrationality measures for 367 Irrationality measures for 369 370 Irrationality measures for exp(1/v) 363 364 371 377 Irrationality measures for log 370 379 Irrationality of 352 Irrationality of e 352 Isotone mean 231 Isotone multimimensional mean 266 Ivory (1796) 12 196 jacobi 5 10 20 22 28 38 52 65 68 73 74 85 106 143 180 252 261 284 301 306 Jacobi (1829) 36 106 Jacobi's differential equation 20 22 Jacobi's duplication formula for arcsl 260 Jacobi's formula for r4, n) 81 Jacobi's identity 35 Jacobi's imaginary quadratic transformation 73 180 Jacobi's triple-product identity 62 65 66 72 301 306 Jacobi's triple-product identity, corollaries 64 65 Jacobi's triple-product identity, finite form 77 Jacobi's triple-product identity, first proof 62 Jacobian elliptic function 29 Jacobian elliptic function, dn 29 Jacobian elliptic function, en 29 Jacobian elliptic function, half angle formula for en 262 Jacobian elliptic function, half angle formula for sn 30 Jacobian elliptic function, sn 29 57 Jones 339 Joubert 142 Kaltofen and Yui (84) 133 Kanada 224 225 341 Karatsuba 211 Keith (86) 342 Khinchin's theorem 362 371 King (24) 16 18 44 52 59 60 Klein 116 Klein (1897) 349 Klein (79) 7 Klein and Fricke (1892) 116 126 Klein's absolute invariant 115 179 Knuth (81) 203 211 212 218 kronecker 135 293 296 297 Kronecker symbol 293 Kummer 179 Kung and Traub (78) 216 Lagrange 3 82 321 375 Lagrange interpolation formula 321 Laguerre 99 Lambert 99 348 Lambert series 91 99 281 286 288 300 Landau 268 269 Landau (1899) 94 Landau (58) 86 294 Landen 381 Landen transform 17 57 59 Landen transform in terms of elliptic functions 58 Landen transform in terms of theta functions 57 Lang (66) 349 Lang (73) 29 30 116 123 Laplace transform 39 Lattice sums, chemical 288 290 Le Petit Archimede (80) 342 Leach and Scholander (78) 237 legendre 3 10 23 26 152 153 154 178 348 Legendre's relation 24 26 27 49 152 153 Legendre's relation, generalized 178 Legendre's relation, theta function proof 43 Lehmer 264 265 Lehmer (38) 345 Lehmer (71) 247 263 Lehmer (85) 386 Lehmer's means 232 235 263 Lehner (66) 116 Leibniz 339 340 Lemniscate sine 5 28 Length 358 Lengths and measures 358 LeVeque (77) 294 349 Lewin (81) 382 386 Lindemann 274 348 Lindemann (1882) 348 Lindemann's theorem 348 357 Liouville 10 36 116 348 Liouville numbers 351 352 Liouville's function 100 Liouville's principle 54 Liouville's summation principle 36 Lipson (81) 216 Logarithm, approximations to 325 327 328 330 Logarithm, bit complexity 219 222 Logarithm, calculation 220 221 222 223 Logarithm, complex 222 Logarithm, operational complexity 219 222 Logarithm, series for 320 Logarithm, theta function algorithms for 224 Logarithmic mean 234 248 261 Lorenz 287 289 Lucas numbers 95 97 100 287 Machin 339 341 344 Machin's formula 339 340 341 344 MacMahon 67 Madelung's constant 288 292 301 Mahler (31) 359 Mahler (53) 368 Mahler (67) 349 368 Matrix logarithm 224 225 226 Mean 230 231 Mean iterations 243 Mean iterations, algebraic 273—280 Mean iterations, Archimedean 246 Mean iterations, arithmetic-harmonic 4 Mean iterations, Carlson's 257 Mean iterations, Gaussian 246 Mean iterations, harmonic-geometric 4 Mean iterations, Lehmer's 265 Mean iterations, multidimensional 267 Mean iterations, pathology 253 Mean iterations, rates of convergence 251 267 272 Mean iterations, Schlomilch's 268 Mean iterations, Tricomi's 265 Mean, discontinuous 230 238 Mean, equivalent mean 231 Mean, homogeneous 231 266 Mean, isotone 231 266 Mean, strict 230 266 Mean, symmetric 231 266 Mean, trace of 231 Means, classes, Gini 233 264 Means, classes, Heronian 237 269 270 Means, classes, Holder 232 235 263 264 Means, classes, identric 234 Means, classes, Lehmer 232 235 263 Means, classes, logarithmic 234 248 261 Means, classes, Neo-Pythagorean 255 Means, classes, series expansions of 263—266 Means, classes, Stolarsky 233 236 264 Measure of polynomial 359 Meil (83) 250 Meinardus 321 Meinardus conjecture 321 Mellin transform 87 90 289 290 301 Metropolis 341 Mignotte (74) 368 Modular equations 103 315 Modular equations for 315 Modular equations, cubic 104 107 109 110 Modular equations, degree of 125 Modular equations, degree of, of degree 15 314 Modular equations, degree of, of degree 23 133 Modular equations, elliptic 112 Modular equations, endecadic 106 Modular equations, endecadic for 121 140 Modular equations, endecadic for j 123 Modular equations, endecadic, octicity of u-v form 126 134 Modular equations, endecadic, quadratic 109 Modular equations, endecadic, quintic 105 107 109 135 136 297 313 Modular equations, endecadic, septic 106 112 313 Modular equations, endecadic, solvable 310 311 313 Modular equations, endecadic, u-v form 126 127—132 134 Modular functions, 114 118 Modular functions, 114 118 121 133 134 Modular functions, 113 117 Modular transformations 103 Modulus 8 Moebius 100 Mollerup 89 Mordell 187 Mordell (16) 286 Multidimensional Archimedean iteration 267 269 Multidimensional Gaussian iteration 267 268 270 Multidimensional invariance principle 269 Multidimensional mean 266 269 Multiplier 103 105 106 Multiplier of order p 136 Multiplier of order p, cubic 138 144 149 Multiplier of order p, cubic, of degree 13 138 Multiplier of order p, cubic, of degree 17 138 Multiplier of order p, quintic 138 309 Multiplier of order p, septic 138 311 N-monotone 291 Nemeth (77) 321 Neo-Pythagorean means 255 Newman (79) 321 Newman (82) 7 222 223 Newman (85) 7 Newman, M., and Shanks (84) 193 Newton 123 207 208 212 339 343 356 Newton's identities 356 Newton's method 212 214 215 216 217 218 223 Niven (56) 347 348 349 Nome 41 Non-prime invariants 295 Nth convergent 372 Nyvoll (78) 196 Operational complexity 201 Order of convergence 2 Oxtoby (80) 352 pade 320 Pade approximant 319 320 323 325 327 331 359 Partially comparable iterates 247 Partition congruences 84 308 Partition function 67 307 Partitions of natural number 67 Pell's equation 376 Pendulum, period of 8 Pentagonal number 66 67 Perimeter of ellipse 8 168 195—197 Periodic continued fraction 375 Pfaff 250 Phillips (81) 252 Pi, AGM identities 48 52 169 197 Pi, algorithms 46 48 170 171 (175) 222 310 315 335 Pi, approximations to 168 191 192 195 197 Pi, complexity of calculating 219 Pi, computation of 337—342 Pi, cubic iteration 171 174 Pi, general iteration 169 Pi, irrationality 348 352 Pi, irrationality measure 367 Pi, legislation on 342 Pi, mnemonic for 342 Pi, normality of 342 Pi, quadratic algorithm for 50 Pi, quadratic iteration 170 174 Pi, quartic iteration 170 174 Pi, quintic iteration 175 313 Pi, septic iteration 171 174 175 Pi, series for 181—190 Pi, transcendence of 347 348 352 354 Picard 119 Picard's theorem 119 Piecewise monotone 234 Pochhammer symbol 178 Poincare 116 poisson 38 Poisson summation formula 36 89 Polya 86 Prime number theorem 378
Реклама
 |
|
О проекте
|
|
О проекте






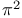
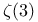
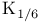 and
and 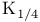
 of order p
of order p