Авторизация
Поиск по указателям
Knapp A.W. — Elliptic Curves (MN-40)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Elliptic Curves (MN-40)Автор: Knapp A.W. Аннотация: An elliptic curve is a particular kind of cubic equation in two variables whose projective solutions form a group. Modular forms are analytic functions in the upper half plane with certain transformation laws and growth properties. The two subjects — elliptic curves and modular forms — come together in Eichler-Shimura theory, which constructs elliptic curves out of modular forms of a special kind. The converse, that all rational elliptic curves arise this way, is called the Taniyama-Weil Conjecture and is known to imply Fermat's Last Theorem.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1992Количество страниц: 448Добавлена в каталог: 05.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Abelian, subvariety 368 Abelian, variety 367 Abel’s theorem 318 Addition 162 363 Addition, elliptic curve 11 Addition, formula 76 Adeles 407 Admissible change of variable 63 363 Affine algebraic set 342 Affine coordinate ring 342 Affine curve 25 343 Affine local coordinates 21 345 Affine problem 3 Affine variety 342 Algebraic integer 122 123 Algebraic numbers 122 Algebraic set, affine 342 Algebraic set, projective 344 Analytic continuation 166 167 Arithmetic-geometric mean 185 402 Associate Dirithlet characters 213 Associativity 12 67 Atkin — Lehner theorem 283 289 Automorphic function 333 Automorphic L function xi 208 Bad prime 108 Bezout’s Theorem 27 47 Birational map 348 Birch and Swinnerton-Dyer conjecture 17 208 386 Canonical class 316 361 Canonical height 35 97 Canonical structure 333 341 349 357 Carayol 391 Change of variables, admissible 63 362 CHARACTER 200 Chord case 75 Chord-tangent composition rule 11 43 Class group, divisor 316 361 Class group, ideal 127 Class number 126 Complex multiplication 164 407 Complex torus 160 183 370 Conductor 213 390 Congruence subgroup 250 256 Congruent numbers 52 110 112 115 conic 25 Continuation, analytic 166 167 Convergent product 195 Coordinate ring 342 Coordinates, affine local 345 Correspondence 385 Cubic 25 40 56 Cubic, nonsingular 58 Cubic, singular 58 Curve, affine 25 343 Curve, elliptic 42 Curve, nonsingular 27 Curve, projective 345 Curve, projective plane 24 Curve, same 24 Curve, singular 27 Curve, smooth 27 Cusp 77 262 Cusp form 225 261 Defined at 344 346 348 Defined over 342 344 347 361 362 368 Degenerate 68 Degree 243 249 273 317 359 360 Descent 80 Differential holomorphic 313 Differential invariant 314 Differential meromorphic 312 DIMENSION 343 346 Dimension formula 235 272 Diophantus 3 6 7 10 50 Diophantus method 6 10 115 118 Dirichlel character 20 Dirichlel character, associate 213 Dirichlel character, conductor of 313 Dirichlel character, extension 113 Dirichlel character, primitive 213 Dirichlel character, principal 201 Dirichlel L function xii 201 Dirichlet series 192 Dirichlet unit theorem 125 Dirichlet’s Theorem xii 148 189 Discrete valuation ring 351 Discriminant 15 58 58 125 226 Divisor 316 360 Divisor class group 316 361 Divisor, principal 316 360 Dominant morphism 343 Dominate 392 Double series theorem 158 Doubling formula 76 Doubly penodir 1 52 Dual isogeny 309 365 Eichler — Shimura theory xii 302 374 388 390 404 Eigenform 280 Elliptic curve 13 42 160 183 362 Elliptic curve, modular 221 Elliptic element 303 Elliptic function 152 Elliptic integral 174 Elliptic regulator 106 Equivalent eigenform 280 Equivalent ideals 126 Euler product 196 202 245 282 289 285 Euler product, irst degree 197 Euler product, second degree 198 Even total winding number 170 Extension of Dirichlet character 213 Fairly bad prime 108 Fermat 52 110 112 Fermat’s Last Theorem xii 3 18 50 54 58 81 397 390 Fermat’s method of descent 80 Fermat’s problem for Mersenne 55 119 fibonacci 52 First degree Euler product 197 Flex 35 Fourier inversion formula 200 210 Fourier transform 200 310 Frey — Serre — Ribet xii 18 399 Frobenius morphism 360 384 Frobenius morphism, 360 Function element 166 Function field 312 319 342 346 Function field of dimension 1 349 Functional equation 209 216 240 270 289 386 387 388 Fundamental domain 228 260 Fundamental parallelogram 152 Gauss 18 5 402 Gauss sum 214 387 Genus 272 117 961 395 Global minimal 290 Good prime 108 Haase — Minkowski theorem 5 Hacke operator 244 275 320 321 323 372 Hasse principle 5 15 16 Hasse — Weil conjecture 18 387 Hasse — Weil L function 403 Hasse’s theorem 16 296 Hecke subgroup 256 Hecke — Petersson theorem 255 282 Hecke’s theorem 349 279 Height 95 97 Hessian matrix 30 Hilbert basis theorem 342 Hilbert nullstellensatz 342 Holomorphic at 225 Holomorphic at the cusp 261 263 Holomorphic differential 312 Homogeneous 243 273 Homogeneous ideal 344 Homogeneous polynomial 22 Homology 317 321 392 Homomorphism 368 Ideal class group 127 Identity, elliptic curve 11 Igusa 374 390 Inflection point 32 Integral, elliptic 174 Intersection multiplicity 32 Invariant differential 314 inversion 269 285 Inversion problem 165 Irreducible 342 345 Isogenous 365 369 Isogeny 164 309 363 369 Isogeny, dual 309 369 Isomorphic elliptic curves 63 Isomorphic over 349 Isomorphic varieties 349 Isomorphism 368 J-invariant 65 226 Jacobi inversion theoren 319 Jacobian variety 310 318 361 369 370 L function xi 17 201 238 267 295 L function, automorphic xi 208 L function, Dirichlet xii 201 L function, mulivic xi 207 Langlands program xiii Lattice 343 318 Legendre symbol 373 298 393 Legendre’s theorem 5 Level 261 333 390 Lie group 376 Line 19 25 Line, at infinity 19 Line, same 19 Line, tangent 27 Linear system 316 361 Liouville theorem, 152 153 Local coordinate, affine 21 345 Local L factor 294 Local ring 343 346 Lutz — Nagell theorem xi 15 130 144 Major’s theorem 15 Mellin transform 238 Meromorphic differential 312 Mestre — Oesterle 396 Method of descent 80 Method of Diophantus 6 10 115 119 Minimal Weierstraas equation 290 Minimal Weierstraas equation at prime p 290 Minimal Weierstraas equation, global 290 Minkowski 5 104 Model 938 341 349 357 Modular elliptic curve 221 Modular form 234 335 261 Modular form, unrestricted 224 261 Modular pair 273 Modular parametrization 310 390 Modular polynomial 335 Mordell — Weil theorem xi 80 95 402 Mordell’s theorem xi 14 80 95 402 Morphism 348 356 Morphism, dominant 349 Morphism, Frobenius 360 384 Motivic L funclion xi Multiplicative 196 Multiplicative, strictly 197 Multiplicity one theorem 283 Multiplicity, intersection 32 Nagell xi 15 130 144 Naive height 95 Negative 12 Newform 283 Newton 10 Node 77 Noetherian 342 Nondegenerate 68 Nonsingular 25 27 58 161 343 347 Nonsplit case 79 Norm 123 Nullstellensatz 342 Number field 122 Odeal of variety 342 344 Oldform 283 Order 153 p-adic filtration 138 p-adic norm 134 p-integral 135 p-reduced 135 Parabolic element 303 Parallelogram, fundamental 152 Parallelogram, period 152 Period 151 184 Period lattice 153 Period parallelogram 152 Petersson inner product 242 252 280 Plane curve 24 Poincare 13 67 Point of inflection 35 Point, nonsingular 25 343 347 Point, singular 25 77 POINTS 19 25 342 344 Points at infinity 19 Poisson summation formula 211 Pole 300 Prescribed torsion 145 primitive 213 Principal axis theorem 37 Principal congruence subgroup 250 256 Principal Dirichlet character 201 Principal divisor 316 360 Product of ideals 126 Product of varieties 347 Product, convergent 195 Projective, algebraic art 344 Projective, closure 345 Projective, curve 345 Projective, n-space 344 Projective, plane 19 Projective, plane curve 24 Projective, problem 3 Projective, transformation 20 345 Projective, variety 345 Purely inseparable 358 Pythagorean triple 7 q-exparwton 225 263 265 Quadratic residue symbol 272 298 393 Ramified 359 Rank 15 102 107 Rational map 347 Rational points 19 25 342 344 Reciprocal roots 196 Reduction modulo p 130 134 364 Regular 344 346 348 Regulator 100 Remann surface 170 311 312 316 Representation theory xiii 407 Result of rearranging 167 Resultant 44 Ribet xii 18 396 399 Riemann xeta function 189 194 Riemann — Roch theorem 317 361 Same curve 24 Same line 19 Schwartz function 211
Реклама
 |
|
О проекте
|
|
О проекте



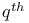 power
power 