|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) Ч The Thirteen Books of Euclid's Elements, Vol. 2 |
|
|
 |
| ѕредметный указатель |
Adrastus 292
Alcinous 98
Alternate and alternately (of ratios) 134
Alternative proofs that in III. 10 claimed by Heron 23Ч24
Alternative proofs, interpolated (cf. 111. 9 and following) 22
Amaldi, Ugo 30 126
Ambiguous case of VI. 7 208Ч209
an-Nairizi 5 16 28 34 36 44 47 302 320
Anaximander 111
Anaximenes 111
Angle, angles not less than two right angles not recognised as angles (cf. Heron, Proclus, Zenodorus) 47Ч49
Angle, controversies about Уangle of semicircleФ and hornlike angle 39Ч42 (see also УHornlikeФ)
Angle, did Euclid extend УangleФ to angles greater than two right angles in VI. 33? 275Ч276
Angle, hollow-angled figure (the re-entrant angle was exterior) 48
Angle, hornlike angle 4 39 40
Angle, Уangle of semicircleФ and Уof segmentФ 4
Antecedents (leading terms in proportion) 134
Antiparallels, may be used for construction of VI. 12 215
Apollonius 75 190 258
Apollonius lemma by Pappus on 64Ч65
Apollonius Plane 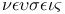 , problem from 81 , problem from 81
Apollonius Plane Loci, theorem from (arising out of Eucl. VI. 3), also found in Aristotle 198Ч200
Application of areas (including exceeding and falling short) corresponding to solution of quadratic equations 187 258Ч260 263Ч265 266Ч267
Approximations to  (Archimedes) 119 (Archimedes) 119
Approximations to \sqrt{4500} (Theon of Alexandria) 119
Approximations, 7/5 as approximation to 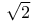 (Pythagoreans and Plato) 119 (Pythagoreans and Plato) 119
Approximations, approximations to 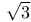 in Archimedes and (in sexagesimal fractions) in Ptolemy 119 in Archimedes and (in sexagesimal fractions) in Ptolemy 119
Archimedes 136 190
Archimedes approximations to 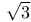 , square roots of large numbers and to , square roots of large numbers and to  119 119
Archimedes extension of a proportion in commensurables to cover incommensurables 193
Archimedes, Liber assumptorum, proposition from 65
Archimedes, new fragment of 40
Archytas proof that there is no numerical geometric mean between n and n+1 295
Aristotle has locus-theorem (arising out of Eucl. VI. 3) also given in ApolloniusТ Plane Loci 198Ч200
Aristotle indicates proof (pre-Euclidean) that angle in semicircle is right 63
Aristotle on alternate ratios 134
Aristotle on composite numbers as plane and solid 286 288 290
Aristotle on def. of same ratio (=same  ) 120Ч121 ) 120Ч121
Aristotle on definions of odd and even by one another 281
Aristotle on inverse ratio 134 149n
Aristotle on non-applicability of arithmetical proofs to magnitudes if these are not numbers 113
Aristotle on number 280;
Aristotle on prime numbers 284Ч285
Aristotle on proportion as Уequality of ratios 119
Aristotle on proportion in three terms ( , continuous) and in four terms ( , continuous) and in four terms ( , discrete) 131 293 , discrete) 131 293
Aristotle on representation of numbers by pebbles forming figures 288
Aristotle on theorem in proportionnot proved generally till his time 113
Aristotle on unit 279
Aristotle, similar rectilineal figures 188
Arithmetic, Elements of, anterior to Euclid 295
at-Tusi see УNasiraddlnФ
August, E. F. 23 25 149 238 256 412
Austin, W. 172 188 211 259
Axioms tacitly assumed in Book V. 137
Axioms tacitly assumed in Book VII. 294
Babylonians 112
Baermann, G.F. 213
Baltzer, R. 30
Barrow 56 186 238
Barrow on Eucl. V. Def. 3 117
Barrow on V. Def. 5 121
Billingsley, H. 56 238
Boethius 295
Borelli, G.A. 2 84
Breadth (of numbers) = second dimension or factor 288
Briggs, H. 143
Camerer, J.G. 22 25 28 33 34 40 67 121 131 189 213 244
Campanus 28 41 56 90 116 119 121 146 189 211 234 235 253 275 320 322 328
Candalla 189
Cantor, Moritz 5 40 97
Cardano, Hieronimo 41
Case, Greeks did not infer limiting cases, but proved them separately 75
Casey, J. 227
Circle, circles intersecting and touching, difficulties in EuclidТs treatment of 25Ч27 28Ч29
Circle, circles touching,meaning of definition 3
Circle, definition of equal circles 2
Circle, modern treatment of 30Ч32
Circle, УcircleФ in sense of УcircumferenceФ 23
Clavius 2 41 42 47 49 53 56 67 70 73 130 170 190 231 238 244 271
Commandinus 47 130 190
Componendo ( ), componendo and separando used relatively to each other 168 170 ), componendo and separando used relatively to each other 168 170
Componendo ( ), denoting УcompositionФ of ratios q.v. ), denoting УcompositionФ of ratios q.v.
Composite numbers in Euclid 286
Composite numbers in Euclid, plane and solid numbers species of 286
Composite numbers in Euclid, with Eucl. and Theon of Smyrna may be even, but with Nicom. and Iambl, are a subdivision of odd 286
Composition of ratios ( ), denoted by componendo ( ), denoted by componendo ( ), distinct from compounding ratios 134Ч135 ), distinct from compounding ratios 134Ч135
Compound ratio, compounded ratios in V. 20Ч23 176Ч178
Compound ratio, explanation of 132Ч133
Compound ratio, interpolated definition of 189Ч190
Consequents (УfollowingФ terms in proportion) 134 238
Continuous proportion ( or or  ) in three terms 131 ) in three terms 131
Conversion of ratio ( ), denoted by convertendo ( ), denoted by convertendo ( ) 135 ) 135
Conversion of ratio (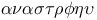 ), denoted by convertendo ( ), denoted by convertendo ( ), convertendo theorem not established by Por. 174Ч175 ), convertendo theorem not established by Por. 174Ч175
Conversion of ratio (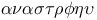 ), denoted by convertendo ( ), denoted by convertendo ( ), convertendo theorem not established by V. 19 ), convertendo theorem not established by V. 19
Conversion of ratio (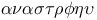 ), denoted by convertendo ( ), denoted by convertendo ( ), convertendo theorem proved by SimsonТs Prop. E 175 ), convertendo theorem proved by SimsonТs Prop. E 175
Convertendo denoting УconversionФ of ratios q.v.
Corresponding magnitudes 134
Cube, cube number, def. of 291
Cube, duplication of, reduced by Hippocrates to problem of two mean proportionals 133
Cube, two mean proportionals between two cube numbers 294 364Ч365
Cyclic of a particular kind of square number 291
Cyclomathia of Leotaud 42
Data of Euclid, Def. 2 248
Data of Euclid, Prop. 24 246Ч247
Data of Euclid, Prop. 55 254
Data of Euclid, Prop. 58 263 265
Data of Euclid, Prop. 67 assumes part of converse of SimsonТs Prop. (Book VI.) 224
Data of Euclid, Prop. 70 250
Data of Euclid, Prop. 8 249Ч250
Data of Euclid, Prop. 85 264
Data of Euclid, Prop. 87 228
Data of Euclid, Prop. 93 227
Data of Euclid, Props. 56 and 68 249
Data of Euclid, Props. 59 and 84 266Ч267
De Morgan, A. 5 7 9Ч10 11 15 20 22 29 56 76Ч77 83 101 104 116Ч119 120 130 139 145 197 202 217Ч218 232 233 234 272 275
De Morgan, A. means of expressing ratios between incommensurables by approximation to any extent 118Ч119
De Morgan, A. on compound ratio 132Ч133 234
De Morgan, A. on definition of ratio 116Ч117
De Morgan, A. on extension of meaning of ratio to cover incommensurables 118
De Morgan, A. on nessity of proof that tests for greater and less, or greater and equal, ratios cannot coexist 130Ч131 157
De Morgan, A., defence and explanation of V. Def. 5 122Ч124
De Morgan, A., proposed lemma about duplicate ratios asalternative means of proving VI. 22 246Ч247
De Morgan, A., sketch of proof of existence of fourth proportional (assumed in V. 18) 171
Dechales 259
DedekindТs theory of irrational numbers corresponds exactly to Eucl. V. Def. 5 124Ч126
Democritus, On difference of gnomon etc. (? on Уangle of contactФ) 40
Democritus, On difference of gnomon etc., on parallel and infinitely near sections of cone 40
Democritus, On difference of gnomon etc., stated, without proving, propositions about volumes of cone and pyramid 40
Dercyllides 111
Diorismns for solution of a quadratic 259
Discrete proportion,  or or  , in four terms 131 293 , in four terms 131 293
Dividendo (of ratios) see УSeparationФ УSeparandoФ
Divisions (of figures), On, treatise by Euclid, proposition from 5
Dodecahedron, decomposition of faces into elementary triangles 98
Dodgson, C.L. 48 275
Duplicate ratio 133
Duplicate ratio,  , duplicate, distinct from , duplicate, distinct from 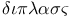 , double (=ratio 2:1), though use of terms not uniform 133 , double (=ratio 2:1), though use of terms not uniform 133
Duplicate ratio, lemma on duplicate ratio as alternative to method of VI. 22 (De Morgan and others) 242Ч247
Duplicate ratio, УduplicateФ of given ratio found by VI. 11 214
Duplication of cube, reduction of, by Hippocrates, to problem of finding two mean proportionals 133
Duplication of cube, wrongly supposed to be alluded to in Timaeus 32 A, B 294Ч295n.
Egyptians 112
Egyptians, Egyptian view of number 280
Enriques (F.) and Amaldi (U.) 30 126
Equimultiples should include once each magnitude 145
Equimultiples, stereotyped phrase Уother, chance, equimultiplesФ 143Ч144
Equimultiples, Уany equimultiples whateverФ,  120 120
Eratosthenes measurement of obliquity of ecliptic ( ) 111 ) 111
Escribed circles of triangle 85 86Ч87
Eudemus 99 111
| Eudoxus 99 280 295
Eudoxus, discovered general theory of proportionals covering incommensurables 112Ч113
Eudoxus, was first to prove scientifically the propositions about volumes of cone and pyramid 40
Eutocius gives locustheorem from ApolloniusТ Plane Loci 198Ч200
Eutocius on УVI. Def. 5Ф and meaning of  116 132 189Ч190 116 132 189Ч190
Even (number), definitions by Pythagoreans and in Xicomachus 251
Even (number), definitions of odd and even by one another unscientific (Aristotle) 281
Even (number), Nicom. divides even into three classes (1) even-times even and (2) eventimes odd as extremes, and (3) odd-times even as intermediate 282Ч283
Even-times even, EuclidТs use differs from use by Nicomachus, Theon of Smyrna and Iamblichus 281Ч282
Even-times odd in Euclid different from even-odd of Nicomachus and the rest 282Ч284
Ex aequali of ratios 136
Ex aequali of ratios, ex aequoii propositions (V. 20, 22), and ex aequali Уin perturbed proportionФ (V. 21, 23) 176Ч178
Faifofer 126
Fourth proportional, assumption of existence of, in V. 18, and alternative methods for avoiding (Saccheri, De Morgan, Simson, Smith and Bryant) 170Ч174
Fourth proportional, Clavius made the assumption an axiom 170
Fourth proportional, condition forexistence of number which is fourth proportional to thiee numbers 409Ч411
Fourth proportional, sketch of proof of assumption by De Morgan 171
Galileo Galilei, on angle of contact 42
Geometric means 357sqq.
Geometric means, one mean between square numbers 294 363
Geometric means, one mean between square numbers or similar plane numbers 371Ч372
Geometric means, two means between cube numbers 294 364Ч365
Geometric means, two means between cube numbers or between similar solid numbers 373Ч375
Geometrical progression 346sqq.
Geometrical progression, summation of n terms of (IX. 35) 420Ч421
Gherard of Cremona 47
Gnomon (of numbers) 289
Golden section (section in extreme and mean ratio), discovered by Pythagoreans 99
Golden section (section in extreme and mean ratio), discovered by Pythagoreans, theory carried further by Plato and Eudoxus 99
Greater ratio, arguments from greater to less ratios etc. unsafe unless they go back to original definitions (Simson on V. 10) 156Ч157
Greater ratio, EuclidТs criterion not the only one 130
Greater ratio, test for, cannot coexist with test for equal or less ratio 130Ч131
Greatest common measure, EuclidТs method of finding corresponds exactly to ours 118 299
Greatest common measure, Nicomachus gives the same method 300
Gregory, D. 116 143
Habler, Th. 294n.
Hankel, H. 116 117
Hauber, C.F. 244
Heiberg, J.L. passim
Henrici and Treutlein 30
Heron of Alexandria 5 16Ч17 24 28 34 36 44 116 189 302 320 383 395
Heron of Alexandria does not recognise angles equal to or greater than two right angles 47Ч48
Heron of Alexandria proof of formula for area of triangle,  87Ч88 87Ч88
Heron of Alexandria, Eucl. III. 12, interpolated from 28
Heron of Alexandria, extends III. 20, 21, to angles in segments less than semicircles 47Ч48
Hippasus 97
Hippocrates of Chios 133
Hornlike angle ( ) 4 39 40 ) 4 39 40
Hornlike angle ( ), Campanus (Уnot angles in same senseФ) 41 ), Campanus (Уnot angles in same senseФ) 41
Hornlike angle ( ), Cardano (quantities of different orders or kinds), Peletier (hornlike angle no angle, no quantity, nothing; angles of all semicircles right angles and equal) 41 ), Cardano (quantities of different orders or kinds), Peletier (hornlike angle no angle, no quantity, nothing; angles of all semicircles right angles and equal) 41
Hornlike angle ( ), Clavius 42 ), Clavius 42
Hornlike angle ( ), Democritus may have written on hornlike angle 40 ), Democritus may have written on hornlike angle 40
Hornlike angle ( ), hornlike angle and angle of semicircle, controversies on 39Ч42 ), hornlike angle and angle of semicircle, controversies on 39Ч42
Hornlike angle ( ), Proclus on 39Ч40 ), Proclus on 39Ч40
Hornlike angle ( ), Vieta and Galileo (Уangle of contact no angleФ) 42 ), Vieta and Galileo (Уangle of contact no angleФ) 42
Hornlike angle ( ), Waliis (angle of contact not inclination at all but degree if curvature) 42 ), Waliis (angle of contact not inclination at all but degree if curvature) 42
Hultsch, F. 133
Iamblichus 97 116 279 280 281 283 284 285 286 287 288 289 290 291 292 293 419
icosahedron 98
Incommensurables approximations to 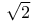 (by means of side- and diagonal-numbers 119 (by means of side- and diagonal-numbers 119
Incommensurables approximations to 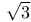 and to and to  , tig; to \sqrt{4500} by means of sexagesimal fractions 119 , tig; to \sqrt{4500} by means of sexagesimal fractions 119
Incommensurables means of expression consist in power of approximation without limit (De Morgan) 119
Incommensurables method of testing incommensurability (process of finding G.C.M.) 118
Incomposite (of number) = prime 284
Ingrami, G. 30 126
Inverse (ratio), inversely ( ) 134 ) 134
Inverse (ratio), inversely ( ), inversion is subject of V. 4, Por. (Theuii) 144 ), inversion is subject of V. 4, Por. (Theuii) 144
Inverse (ratio), inversely ( ), inversion is subject of V. 7, Por 149 ), inversion is subject of V. 7, Por 149
Inverse (ratio), inversely ( ), is not properly put in either place 149 ), is not properly put in either place 149
Inverse (ratio), inversely ( ), SimsonТs Prop. B on directly deducibie from V. Def. 5 144 ), SimsonТs Prop. B on directly deducibie from V. Def. 5 144
Isosceles triangle of IV. 10, construction of, by Pythagoreans 97Ч99
Jacobi, C.F.A. 1S8
Lachlan, R. 226 227 245Ч246 247 256 272
Lardner, D. 58 259 271
Least common multiple 336Ч341
legendre 30
Legendre proves VI. 1 and similar propositions in two parts: (1) for commensurables, (2) for incommensurables 193Ч194
Lemma assumed in VI. 22 242Ч243
Lemma assumed in VI., alternative propositions on duplicate ratios and ratios of which they are duplicate (De Morgan and others) 242Ч247
Length,  (of numbers in one dimension) 287 (of numbers in one dimension) 287
Length,  (of numbers in one dimension), Plato restricts term to side of complete square 287 (of numbers in one dimension), Plato restricts term to side of complete square 287
Leotaud, Vincent 42
Linear (of numbers) = (1) in one dimension 287
Linear (of numbers) = (2) prime 285
Logical inferences, not made by Euclid 22 29
Lucian 99
Means, geometric mean is Уproportion par excellenceФ ( ) 292Ч293 ) 292Ч293
Means, no numerical geometric mean between n and n+1 (Archytas and Euclid) 295
Means, one geometric mean between similar plane numbers, two between similar solid numbers 371Ч375
Means, one geometric mean between two square numbers, two between two cube numbers (Plato) 294 363Ч365
Means, three kinds, arithmetic, geometric and harmonic 292Ч293
Moderatus, a Pythagorean 280
Multiplication, definition of 287
Musici Scriptores Graeci 295
Nasiraddin at-Tusi 28
Nesseimann, G.H.F. 287 293
Nicomachus 116 119 131 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 300 363
Nixon, R.C.J. 16
Number, defined by Nicomachus and Iamblichus on 280
Number, defined by Thales, Eudoxus, Moderatus, Aristotle, Euclid 280
Number, represented by lines 288
Number, represented by lines and by points or dots 288Ч289
Oblong (of number) in Plato either  or or 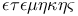 288 288
Oblong (of number), but these terms denote two distinct divisions of plane numbers in Nicomachus, Theon of Smyrna and Iamblichus 289Ч290
octahedron 98
Odd (number), def. of odd and even by one another unscientific (Aristotle) 281
Odd (number), defs. of in Nicomachus 281
Odd (number), Nicom. and Iambl, distinguish three classes of odd numbers (1) prime and incomposite, (2) secondary and composite, as etremes, (3) secondary and composite in itself but prime and incomposite to one another, which is intermediate 257
Odd (number), Pythagorean definition 281
Odd-times even (number), definition in Eucl. spurious 283Ч284
Odd-times even (number), definition in Eucl. spurious and differs from definitions by Nicomachus etc. ibid.
Odd-times odd (number), defined in Eucl. but not in Nicom. and Iambi 284
Odd-times odd (number), Theon of Smyrna applies term to prime numbers 284
Oenopides of Chios 111
Pappus 4 27 29 67 79 81 113 133 211 250 251 292
Pappus assumes case of VI. 3 where external angle bisected (SimsonТs VI. Prop. A) 197
Pappus lemma on ApolloniusТ Plane 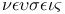 64-65 64-65
Pappus problem from same work 81
Pappus theorem from ApoiloniusТ Plane Loci 198
Pappus theorem that ratio compounded of ratios of sides is equal to ratio of rectangles contained by sides 250
Peletarius 47 56 84 146 190
Peletarius (Peletier) on angle of contact and angle of semicircle 41
Pentagon decomposition of regular pentagon into 30 elementary triangles 98
Pentagon relation to pentagram 99
Pentagonal numbers 289
Perturbed proportion (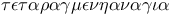 ) 136 176Ч177 ) 136 176Ч177
Pfleiderer, C.F. 2
Philolaus 97
Philoponus 234 282
Plane numbers, product of two factors (УsidesФ or УlengthФ and УbreadthФ) 287-288
Plane numbers, product of two factors (УsidesФ or УlengthФ and УbreadthФ), in Plato either square or oblong 257-258
Plane numbers, product of two factors (УsidesФ or УlengthФ and УbreadthФ), one mean proportional between similar plane numbers 371Ч372
Plane numbers, product of two factors (УsidesФ or УlengthФ and УbreadthФ), similar plane numbers 293
Plato 7/5 as approximation to \sqrt{2} 119
Plato construction of regular solids from triangles 97Ч98
Plato on 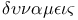 (square roots or surds) 288 290 (square roots or surds) 288 290
Plato on golden section 99
Plato on square and oblong numbers 288 293
Plato theorem that between square numbers one mean suffices, between cube numbers two means necessary 294 364
Playfair, John 2
Plutarch 98 254
Polygonal numbers 289
Porism (corollary) to proposition precedes УQ.E.D.Ф or УQ.E.F.Ф 8 64
Porism (corollary) to proposition precedes УQ.E.D.Ф or УQ.E.F.Ф, Porism to IV. 15 mentioned by Proclus 109
Porism (corollary) to proposition precedes УQ.E.D.Ф or УQ.E.F.Ф, Porism to VI. 19 234
Prime (number) 4 39 40 193 247 269
Prime (number), 2 admitted as prime by Eucl. and Aristotle, but excluded by Nicomachus, Theon of Smyrna and Iamblichus, who make prime a subdivision of odd 284Ч285
Prime (number), Aristotle on two senses of УprimeФ 285:
Prime (number), definitions of 284Ч285
Prime (number), definitions of Уprime to one anotherФ 285Ч282
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



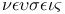 , problem from
, problem from  (Archimedes)
(Archimedes) 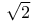 (Pythagoreans and Plato)
(Pythagoreans and Plato) 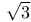 in Archimedes and (in sexagesimal fractions) in Ptolemy
in Archimedes and (in sexagesimal fractions) in Ptolemy  )
)  , continuous) and in four terms (
, continuous) and in four terms ( , discrete)
, discrete)  ), componendo and separando used relatively to each other
), componendo and separando used relatively to each other  ), denoted by componendo (
), denoted by componendo ( or
or  ) in three terms
) in three terms 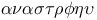 ), denoted by convertendo (
), denoted by convertendo ( )
)  or
or  , in four terms
, in four terms  , duplicate, distinct from
, duplicate, distinct from 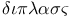 , double (=ratio 2:1), though use of terms not uniform
, double (=ratio 2:1), though use of terms not uniform 
 )
) 

 )
)  )
)  (of numbers in one dimension)
(of numbers in one dimension)  )
)  or
or 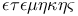
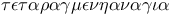 )
) 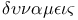 (square roots or surds)
(square roots or surds)