|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Heath T.L. (ed.) Ч The Thirteen Books of Euclid's Elements, Vol. 2 |
|
|
 |
| ѕредметный указатель |
Prime (number), different names for prime, Уodd-times oddФ (Theon), УlinearФ (Theon), УrectilinearФ (Thymaridas), УeuthymetricФ (Iamblichus) 285
Prime (number), prime absolutely or in themselves as distinct from prime to one another (Theon) 285
Prime (number), Уprime and incomposite ( )Ф 284 )Ф 284
Proclus on absence of formal divisions of proposition in certain cases, e.g. IV. 10 100
Proclus on use of УquindecagonФ for astronomy III 4 39 40 193 247 269
Proportion in giving older theory as well Euclid simply followed tradition 113
Proportion, alternatives for v. Def. 5 by a geometer-friend of Saccheri, by Faifofer, Ingrami, Veronese, Enriques and Amaldi 126
Proportion, Aristotle on general proof (new in his time) of theorem (alternando) in proportion 113
Proportion, complete theory applicable to incommensurables as well as commensurables is due to Eudoxus 112
Proportion, De Morgan on extension of meaning of ratio to cover incommensurables 118
Proportion, De MorganТs defence of V. Def. 5 as necessary and sufficient 122Ч124
Proportion, definition in V. Def. 5 substituted for that of VII. Def. 20 because latter found inadequate, not vice versa 121
Proportion, extensive use of proportions in Greek geometry 187
Proportion, interpolated definitions of proportion as УsamenessФ or Уsimilarity of ratiosФ 119
Proportion, old (Pythagorean) theory practically represented by arithmetical theory of Eucl. VII 113
Proportion, power of expressing incommensurable ratio is power of approximation without limit 119
Proportion, proportion in three terms (Aristotle makes it four) the УleastФ 131
Proportion, proportionals of VII. Def. 20 (numbers) a particular case of those of V. Def. 5 (SimsonТs Props. C, D and notes) 126Ч129
Proportion, proportions enable any quadratic equation with real roots to be solved 187
Proportion, supposed use of propositions of Book V. in arithmetiPsellus 234
Proportion, three УproportionsФ 292, but proportion par excellence or primary is continuous or geometric 292Ч293
Proportion, V. Def. 5 corresponds to WeierstrassТ conception of number in general and to DedekindТs theory of irrationals 124Ч126
Proportion, X. 5 as connecting two theories 113
Proportion, УcontinuousФ proportion (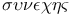 or or  , in Euclid , in Euclid  ) 131 293 ) 131 293
Proportion, УdiscreteФ or УdisjoinedФ ( ) 131 293 ) 131 293
Proportion, УorderedФ proportion ( ), interpolated definition of 137 ), interpolated definition of 137
Proportion, УperturbedФ proportion ( ) 136 176Ч177 ) 136 176Ч177
Ptolemy, Claudius 111 117 119
Ptolemy, Claudius, lemma about quadrilateral in circle (SimsonТs VI. Prop. D) 225Ч227
Pyramidal numbers 290
Pyramidal numbers, pyramids truncated, twice-truncated etc. 291
Pythagoras construction of figure equal to one and similar to another rectilineal figure 254
Pythagoras introduced Уthe most perfect proportion in four terms and specially called УharmonicФФ into Greece 112
Pythagoras, reputed discoverer of construction of five regular solids 97
Pythagoreans called 10 УperfectФ 294
Pythagoreans distinguished three sorts of means, arithmetic, geometric, harmonic 112
Pythagoreans had theory of proportion applicable to commensurables only 112
Pythagoreans of even and odd 281
Pythagoreans theorem about only three regular polygons filling space round a point 98
Pythagoreans, 7/5 as approximation to 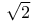 119 119
Pythagoreans, construction of dodecahedron in sphere 97
Pythagoreans, construction of isosceles triangle of IV. 10 and of regular pentagon due to 97Ч98
Pythagoreans, definitions of unit 279
Pythagoreans, possible method of discovery of latter 97Ч99
Quadratic equations exact correspondence of geometrical to algebraical solution 263Ч264 266Ч267
Quadratic equations,  or condition of possibility of solving equation of Eucl. VI. 28 259 or condition of possibility of solving equation of Eucl. VI. 28 259
Quadratic equations, but method gives both roots if real 258
Quadratic equations, one solution only given, for obvious reasons 260 264 267
Quadratic equations, solution by means of proportions 187 263Ч265 266Ч267:
Quadrilateral condition for inscribing circle in 93 95
Quadrilateral in circle, PtolemyТs lemma on (SimsonТs VI. Prop. D) 225Ч227
Quadrilateral inscribing in circle of quadrilateral equiangular to another 91Ч92
quadrilateral not a УpolygonФ 239
Radius, no Greek word for 2
Ratio ex aequali 136
Ratio ex aequali in perturbed proportion 136
Ratio, alternate ratio, alternando 134
Ratio, arguments about greater and less ratios unsafe unless they go back to original definitions (Simson on V. 10) 156Ч157
Ratio, BarrowТs defence of it 117
Ratio, composition of ratio, componendo, different from compounding ratios 134Ч135
Ratio, compound ratio 132Ч133 189Ч190 234
Ratio, conversion of ratio, convertendo 135
Ratio, def. of greater ratio only one criterion (there are others) 130
Ratio, definition of 116Ч119 110
Ratio, division of ratios used in Data as general method alternative to compounding 249Ч250
Ratio, duplicate, triplicate etc. ratio as distinct from double, triple etc 133
Ratio, inverse ratio, inversely 134
Ratio, means of expressing ratio of incommensurables is by approximation to any degree of accuracy 119
Ratio, method of transition from arithmetical to more general sense covering incommensurables 118
Ratio, names for particular arithmetReciprocal or reciprocally related figures: definition spurious 189
Ratio, operation of compounding ratios 234
Ratio, separation of ratio, separando (commonly dividendo) 135
Ratio, sufficient ground for regarding it as spurious 117
Ratio, test for greater ratio easier to apply than that for equal ratio 129Ч130
Ratio, tests for greater equal and less ratios mutually exclusive 130Ч131
Ratio, Уratio compounded of their sidesФ (careless expression) 248
Reductio ad absurdum, the only possible method of proving III. 1 8
Saccheri, Gerolamo 126 130
Saccheri, Gerolamo, proof of existence of fourth proportional by VI. 1, 2, 12 170
Savile, H. 190
Scalene, a class of solid numbers 290
Scholia, IV. No. 2 ascribes Book IV. to Pythagoreans 97
| Scholia, V. No. 1 attributes Book V. to Eudoxus 112
Scholiast to Clouds of Aristophanes 99
Sectio canonis of Euclid 295
Sector (of circle), explanation of name, two kinds (1) with vertex at centre, (2) with vertex at circumference 5
Sector-like (figure) 5
Sector-like (figure), bisection of such a figure by straight line 5
Segment of circle, angle of 4
Segment of circle, similar segments 5
Semicircle, angle of 4 39Ч41 see
Semicircle, angle of, angle in semicircle a right angle, pre-Euclidean proof 63
Separation of ratio,  , and separando ( , and separando ( ) 135 ) 135
Separation of ratio,  , and separando ( , and separando ( ), separando and componendo used relatively to one another, not to original ratio 168 170 ), separando and componendo used relatively to one another, not to original ratio 168 170
Sides of plane and solid numbers 287Ч288
Similar plane and solid numbers 293
Similar plane and solid numbers, one mean between two similar plane numbers 371Ч372
Similar plane and solid numbers, two means between two similar solid numbers 294 373Ч375
Similar rectilineal figures, def. gives at once too little and too much 188
Similar rectilineal figures, def. of, given in Aristotle 188
Similar rectilineal figures, similar figures on straight lines which are proportional are themselves proportional and conversely (VI. 22), alternatives for proposition 242Ч247
Similar segments of circles 5
Simon, Max 124 134
SIMPSON, THOMAS 121
Simson, R. 2 3 8 22 23 33 34 37 43 49 53 70 73 79 90 ll7 131 132 140 143Ч144 145 146 148 154 161 162 163 165 170Ч172 177 179 180 182 183 184 185 l86 189 I93 I95 209 211 212 230Ч231 238 252 269 270 272-273
Simson, R., Axioms to Book V. 137
Simson, R., Book VI. Prop. A extending VI. 3 to case where external angle bisected 197
Simson, R., important note showing flaw in V. 10 and giving alternative 156Ч157
Simson, R., Prop. B (inversion) 144
Simson, R., Prop. E (convertendo) 175
Simson, R., Props. B, C, D 222Ч227
Simson, R., remarks, on VI. 27Ч29 258Ч259
Simson, R., shortens V. 8 by compressing two cases into one 152Ч153
Simson, R.: Props. C, D (Book V.) connecting proportionals of VII. Def. 20 as particular case with those of V. Def. 5 126Ч129
Size, proper translation of  in V. Def. 3 116Ч117 189Ч190 in V. Def. 3 116Ч117 189Ч190
Smith and Bryant, alternative proofs of V, 16, 17, 18 by means of VI. 1, where magnitudes are straight lines or rectilineal areas 165Ч166 169 173Ч174
Solid numbers, three varieties according to relative length of sides 290Ч291
Spherical number, a particular kind of cube number 291
Square number, product of equal numbers 289 291
Square number, product of equal numbers, one mean between square numbers 294 363Ч364
Stobaeus 280
Subduplicate of any ratio found by VI. 13 216
Swinden, J.H. van 188
Tacquet, A. 121 258
Tannery, P. 112 113
Tartaglia, Niccolo 2 47
Taylor, H.M. 16 22 29 56 75 102 227 244 247 272
tetrahedron 98
Thales 111 280
Theodosius 37
Theon of Alexandria 43 109 117 119 149 152 161 186 190 234 235 240 242 250 262 311 322 412
Theon of Alexandria interpolation in V. 13 and Porism 144
Theon of Alexandria, additions to VI. 33 (about sectors) 274Ч276
Theon of Alexandria, interpolated Porism to VI. 20 239
Theon of Smyrna, in 119 279 280 281 284 285 286 288 289 290 291 292 293 294
Thrasyllus 292
Thymaridas 279 285
Timaeus of Plato 97Ч98 294Ч295 363
Todhunter, I. 3 7 22 49 51 52 67 73 90 99 172 195 202 204 208 259 271 272 300
Trapezium, name applied to truncated pyramidal numbers (Theon of Smyrna) 291
Triangle, HeronТs proof of expression for area in terms of sides, 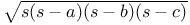 87Ч88 87Ч88
Triangle, right-angled triangle which is half of equilateral triangle used for construction of tetrahedron, octahedron and icosahedron (Timaeus of Plato) 98
Triangular numbers 289
Triplicate, distinct from triple, ratio 133
Unit,  connected etymologically by Theon of Smyrna and Nicomachus with connected etymologically by Theon of Smyrna and Nicomachus with  (solitary) or (solitary) or  (rest) 279 (rest) 279
Unit, definitions of, by Thymaridas, Уsome Pythagoreans,Ф Chrysippus, Aristotle and others 279
Unit, EuclidТs definition was that of the Уmore recentФ writers 279
Veronese, G. 30 126
Vieta, on angle of contact 42
Walker 204 208 259
Wallis, John, on angle of contact (Уdegree of curvatureФ) 42
Weierstrass 124
Woepcke 5
Zenodorus 276
УChance equimultiplesФ in phrase Уother, chance, equimultiplesФ 143Ч144
УComposite to one anotherФ (of numbers) 286Ч287
УDissimilarly orderedФ proportion ( ) in Archimedes = Уperturbed proportionФ 136 ) in Archimedes = Уperturbed proportionФ 136
УDivision (of ratios)Ф see УSeparationФ
УOrderedФ proportion ( ), interpolated definition of 137 ), interpolated definition of 137
УParallelepipedalФ (solid) numbers, two of the three factors differ by unity (Nicomachus) 290
УPerfectФ (of a class of numbers) 293Ч294 421Ч425
УPerfectФ (of a class of numbers), 3 also called УperfectФ 294
УPerfectФ (of a class of numbers), Pythagoreans applied term to 10 294:
УQuindecagonФ (fifteen-angled figure), useful for astronomy 111
УRule of threeФ, VI. 12 equivalent to 215
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 )Ф
)Ф 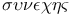 or
or  , in Euclid
, in Euclid  )
)  )
)  ), interpolated definition of
), interpolated definition of  )
) 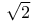
 or condition of possibility of solving equation of Eucl. VI. 28
or condition of possibility of solving equation of Eucl. VI. 28  , and separando (
, and separando ( )
)  in V. Def. 3
in V. Def. 3 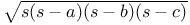
 connected etymologically by Theon of Smyrna and Nicomachus with
connected etymologically by Theon of Smyrna and Nicomachus with  (solitary) or
(solitary) or  (rest)
(rest)  ) in Archimedes = Уperturbed proportionФ
) in Archimedes = Уperturbed proportionФ  ), interpolated definition of
), interpolated definition of