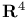|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Nash C. Ч Differential Topology and Quantum Field Theory |
|
|
 |
| ѕредметный указатель |
 -vector bundle 125 -vector bundle 125
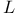 -polynomial 112 340Ч341 -polynomial 112 340Ч341
Abelian differential 143
Abelian gauge theory 295 343Ч344 348
Abelian group 170 185
Abelian representation 325
Abelian semi-group 67 90
Abelian sub-group 188 (see also under Torus)
Adiabatic limit 284 288 290
Adjoint bundle 176
Affine space 216
Alexander polynomial 340Ч342
Algebraic curve 169
Algebraic varieties 137Ч139
Algebraic varieties, sub-manifold of 138
Amp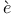 reТs law 344Ч345 reТs law 344Ч345
Analytic torsion 348Ч349
Analytical index 93 97 120 126
Anharmonic ratio 314
anomalies 269Ч300
Anomalies, complex 290Ч291
Anomalies, for strings 281Ч283
Anomalies, global 283Ч290
Anomalies, gravitational 279Ч281
Anomalies, Hamiltonian approach to 292Ч300
Anomalies, local 269Ч283
Anomalous dimension 302
Arithmetic genus 107
Atiyah-singer index theorem 89 90Ч136
Axial current 272
Banach space 48 171
Base point 5Ч6
Base point, and 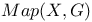 172 172
Base point, and gauge transformations 176 232
Base point, and homotopy 8 10 17Ч18 20
Base point, and K-theory 69Ч70 72
Beltrami differential 157 161
Beltrami equation 157
BesselТs equation 35
Betti number 104 172 192 207
Betti number, and Hodge numbers 108
Betti number, and Laplacians 41 209
Betti number, and Morse theory 194 211
Betti number, and the instanton deformation complex 238
Betti number, and the Poincar series 193 series 193
Betti number, of 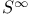 204 204
Betti number, of 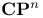 197 197
Bianchi identity 228 243
Bifurcation 198
Bogomolny equation 243Ч246
Bogomolny equation, in hyperbolic space 247Ч251
Borel subgroup 189
Borel-Weil construction 188Ч191
Bott periodicity 11 75 78 95
boundary conditions 127
Boundary conditions, and Floer homology 328 337
Boundary conditions, and monopoles 244
Boundary conditions, non-local and the index theorem 128 131Ч133
Boundary conditions, periodic 311
Bundle automorphisms 175 (see also Gauge transformations)
Callan Ч Symanzik equations 301
Canonical bundle 139 (see also Determinant bundle)
Cartan matrix 24
Casimir operator 181Ч183
Casson invariant 330
Categories see also Lusternik-Schnirelmann category
Categories and conformal field theory 321
Cauchy data 30
Cauchy problem 30
Cauchy Ч Riemann equations 64
Cauchy Ч Riemann operator 34 281
CauchyТs Theorem 29
Cell decomposition 323
Cellular approximation theorem 323
Central charge 174
Central charge, and conformal field theory 307Ч308
Central extensions 179 (see also group extensions)
Central extensions, and the loop group 173 180 183 191
Central extensions, and the Virasoro group 174
Character ring 125
Characteristic class 16 78Ч79 82 85 108 112 133 239 278 280 290
Characteristic class, and invariant polynomials 87
Characteristic class, and obstruction theory 23
Characteristic class, and the index formula 98 101Ч103
Characteristic polynomial 135
Chern character 78Ч80 88 105 237 239 280 282
Chern character, and K-theory 81
Chern character, and the index formula 98
Chern class 16 79Ч82 105Ч106 134 142 180 189 219 222 237 245 248 277 286 297 334
Chern class, and line bundles 145Ч146
Chern class, and the Euler class 87
Chern class, and the Pontrjagin class 84Ч85
Chern Ч Simons see also Knots
Chern Ч Simons, action 331 342Ч344 348 350 358 360
Chern Ч Simons, class 223 227
Chern Ч Simons, form 227
Chern Ч Simons, function 324Ч327 330
Chiral Fermion 270 271
ChowТs theorem 138
Classifying space 16 23
Classifying space and equivariant cohomology 202Ч204
Classifying space, and differentiable structures 19
Classifying space, and Fredholm operators 293
Classifying space, and vector bundles 70Ч71 74
Clifford algebra 114
Clover leaf knot 340Ч341
Cocycle 145 298
Cocycle, and group extensions 179 184Ч185
Cohomology 3 12Ч13 41 65 145 280 283 323 326 333-
Cohomology ring 15Ч16 95 120 220
Cohomology ring, and 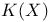 79 79
Cohomology ring, and torsion 195
Cohomology, de Rham see de Rham cohomology
Cohomology, Dolbeault see Dolbeault cohomology
Cohomology, for sheaves see sheaf cohomology
Cohomology, for vector bundles see K-theory
Cohomology, local 279
Compact support 46
Compact support, and K-theory 90Ч91
Compact support, and test functions 50
Compactification 91 334 339
Compactification divisor 319
Complex manifolds 63 65 89 117 189 255 290Ч291
Complex manifolds, and algebraic geometry 138Ч139 142
Complex manifolds, and Morse theory 197
Complex manifolds, and the Dolbeault complex 106Ч108
Complex powers of elliptic operators 46
Complex structure 84 147 190 315 322
Complex structure of Riemann surfaces 139 149Ч155 241
Complex structure, and anomalies 291
Complex structure, and hyperk hler manifolds 255 hler manifolds 255
Complex structure, and strings 260Ч262
Complex structure, and vector bundles 84
Complex vector bundle see under vector bundle
Complexification 83Ч84 98 103 106 120 237
Complexification, of Lie groups 189Ч190
Complexification, of vector bundles 83Ч84
Comultiplication 8
Configuration space, and conformal field theory 320
Configuration space, for instantons 218Ч219 232 242 258
Configuration space, for monopoles 254
Configuration space, for strings 261
Conformal anomaly 180 262 281Ч283
Conformal block 315 317 319 321 321 350 356
Conformal family 309Ч317
Conformal field theory 306Ч321
Conformal field theory, and knot theory 343 350 354Ч355
Conformal Field Theory, rational 313
Conformal invariance 174 247 258 301 311 314 317
Conformal invariance, and conformal field theories 301 311 314 317
| Conformal invariance, and strings 281Ч283
Conformal invariance, and the Virasoro group 174
Conformal invariance, and Yang Ч Mills theories 247 258
Conformal Killing vector 159 262
Conformal weight 312 355
Conjugate bundle 82
Connected sum 335 336 351
Connections see also Instantons and monopoles
Connections, flat 323Ч326 330Ч331
Connections, Levi Ч Civita 270
Connections, projectively flat 320
Connections, reducible 232 240 323
Connections, Yang Ч Mills 118 270 279 281
Continuous section 219
Contractibility 96 156 204 245
Contractibility, and Fredholm operators 293
Contractibility, and universal bundles 96 218Ч219 245 258 327
Coupling constant 273 335 343 345Ч346
Covering space 139 153 156 255
Critical dimension 180 269 281
Critical points 192Ч201 204 206Ч207 209Ч213 301 323
Critical points, and flat connections 323Ч326 330Ч331
Critical points, and instantons 228Ч230
Critical points, and monopoles 242Ч243 255Ч259
Critical points, and phase transitions 301
Critical points, and the Hessian 193
Critical points, non-degenerate 193
Current algebra 173 177Ч178 185 299
De Rham cohomology 3 41 280 283 323 326 333
de Rham cohomology, and loop groups 179
de Rham cohomology, via sheaves 63 65
de Rham complex 13 93 108 116 124 238 323
de Rham complex, index of 103Ч104 106 116
Dedekind  -function 312Ч313 -function 312Ч313
Dehn twist 156 309 355
Descendant of a primary field 309
Determinant bundle 139
Determinant bundle, and index theory 276Ч278 283Ч286
Determinant line bundle see determinant bundle
Diagonalisable matrices 88
Differentiable structure 2 23 26 338Ч339
Differentials of first kind see Abelian differentials
Dilation 301Ч302 308
Dimensional reduction 250
Dirac operators 113Ч114
Dirac operators, and anomalies 269Ч281 283Ч296
Dirac operators, families of 275
Dirac operators, gauge covariance of 271
Dirac operators, index in twisted case 118
Dirac operators, index of 115Ч116
Direct limit 19 57
Discrete series 186
Distributions 49Ч51
Divisor 139Ч142 146
Divisor, and conformal field theory 319
Divisor, and Weierstrass gap theorem 166Ч167
Dolbeault cohomology 65 145
Dolbeault cohomology, and the Riemann moduli space 160
Dolbeault complex 106
Dolbeault complex index of 107 117
DonaldsonТs polynomial invariants 334 336 338Ч339
DonaldsonТs theorem 25Ч26 240Ч241
Doughnut 196Ч197 199
Dual bundle 107
Dyons 256
Effective action 288Ч289
Eilenberg and Steenrod 65
Eilenberg Ч MacLane space 12
Elliptic complex 91Ч96 103Ч104 124 126
Elliptic complex, and instanton moduli 235
Elliptic complex, and monopole moduli 251
Elliptic operators 27Ч55 162 327 348
Elliptic operators, and instanton deformations 237
Elliptic operators, and strings 261Ч268
Elliptic operators, as Fredholm operators 53Ч55
Elliptic operators, definition of differential 33 38
Elliptic operators, definition of pseudo-differential 42Ч43
Elliptic operators, families of 119
Elliptic operators, index theory of 89Ч136
Elliptic operators, of order  45 45
Ellipticity 27Ч33 (see also hypo-ellipticity)
Energy functional 205 326
Energy functional, for geodesics 205
Energy functional, for monopoles 242 255Ч256
Energy momentum tensor 181 335
Energy momentum tensor, of conformal field theories 304 308 319Ч320
Equivariant cohomology 201Ч203
Equivariantly perfect function 204Ч205 258
Euler class 16 86Ч87 103Ч106 117 134 203
Euler Ч Poincar characteristic 3 characteristic 3
Evaluation map 221Ч224
Exceptional groups 170
Exceptional Lie algebra 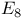 24 24
Exotic differentiable structure 23
Exotic differentiable structure, on 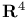 26 26
Exotic sphere 23 192 285Ч286
Exterior algebra 94
Exterior algebra, and Fock space 297
Exterior algebra, and Hopf algebras 221Ч222
External product 76
Extremum 205 (see also Critical points)
Faddeev Ч Popov ghosts 218 347
Fake 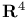 26 26
Families index theorem 119Ч122
Families index theorem for real families 121Ч122 284
Families index theorem, and anomalies 273Ч296
Family see also families index theorem
Family, conformal 309Ч317
Family, of  -bundles 220 -bundles 220
Family, of conformal Killing vectors 165
Family, of connections 224 228 233 241 251Ч252
Family, of elliptic operators 119Ч122 269 275Ч297 326
Family, of Riemann surfaces 139
Family, of supersymmetric algebras 209
Fibration 17Ч19 120
Fibration, and differentiable structures 20Ч22
Fibration, and homotopy lifting property 17
Fibration, automorphism of 175
Fibration, of Hopf 78
Fibre bundle 14Ч19 287
Fibre bundle, and elliptic families 119
Fine sheaf 64 146
Fixed points 123Ч127 150 301
Fixed points, and index theory 123Ч137
Fixed points, of group actions 150 153Ч156 201 217Ч218 232
Flat connections 244 325 346Ч350
Floer homology 321Ч331
Floer homology, and Donaldson invariants 336Ч338
Fock space 297Ч299
Four manifolds 23Ч26 331Ч338
Fourier transform 28 31Ч34 37 44 48 52
Fractional integration 44
Framing of knots 345 354Ч355
Fredholm operators 54Ч55 292Ч294
Fredholm operators, and K-theory 88 292
Fredholm operators, from elliptic operators 53Ч55
Fredholm operators, self-adjoint 293Ч294
Fredholm operators, skew-adjoint 294
Free action 150 232
Fubini Ч Study metric 147
Fuchsian group 161
Functional integral 218 321
Functional integral, and anomalies 271Ч275 288
Functional integral, and Donaldson invariants 336
Functional integral, and knots 344Ч348 351
Functional integral, for strings 260
functors 7 293Ч294
Fundamental group 5Ч6 9Ч10 153Ч154 340
Fundamental solution 28
Fusion rules 313 316Ч317 321
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -vector bundle
-vector bundle 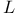 -polynomial
-polynomial 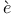 reТs law
reТs law 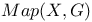
 series
series 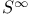
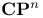
 hler manifolds
hler manifolds  -function
-function