|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Nash C. Ч Differential Topology and Quantum Field Theory |
|
|
 |
| ѕредметный указатель |
Gauge fixing 218 349
Gauge orbits 218 271 323
Gauge system 318
Gauge transformations 175 177 216Ч217 234 257Ч258 269 281 283 297
Gauge transformations, and ellipticity 230
Gauge transformations, generated by the Higgs field 252
Gauss Ч Bonnet theorem 104 134 152 163
GaussТs law 297
Germs 58 (see also sheaves)
Ghosts 218 347
Global anomaly 270 286Ч290 294
Gradient flow 212 327Ч329
Grassmannian 71Ч73
Gravitational anomaly 280 (see also anomalies)
GreenТs function 28Ч30 33 34 344
Gribov ambiguity 219
Group extensions 178Ч185
Group extensions, central 179Ч183
Group extensions, non-central 183Ч185
H-space 8Ч10 12
Hamiltonian and anomalies 291Ч300
Handle 1 139 143 156
Harmonic forms 148
harmonic oscillator 211
Harmonic spinor 115
Heat equation 33Ч35
Heat equation, and the index theorem 132
Height function 196Ч204
hessian 193 197 199 212
Hessian, and the Yang Ч Mills action 258
Hessian, unbounded and Floer theory 325Ч326
Higgs field 248 252Ч253 257
Highest weight representation 186Ч191
Highest weight representation, and conformal field theory 309
Hodge numbers 108 148
Hodge theory 93 110 115 147Ч148 164 332 350
Holomorphic sections 58 139 142 146
Holomorphic sections, and conformal field theory 317
Holomorphic sections, and sheaves 58Ч59
Holomorphic sections, and the Borel-Weil theorem 189Ч191
Holomorphic sections, and the Weierstrass gap theorem 166Ч168
Holonomy group 218 232
Homeomorphisms 2 19 340
Homfly polynomial 341 360
Homology sphere 337Ч338 (see also homology 3-sphere)
Homology, 3Чsphere 323 325 329Ч330 336Ч338
Homotopy classes 5Ч10 16 21 72 88 90
Homotopy equivalence 4 12 221Ч222 293
Homotopy groups 3 7 9Ч14
Homotopy groups, and Fredholm operators 294
Homotopy groups, and gauge transformations 219Ч222
Homotopy groups, and K-theory 72Ч75
Homotopy groups, and obstruction theory 21Ч22
Homotopy lifting property 17Ч18
Homotopy quotient 202Ч203
Homotopy type 4Ч5 12 219
Homotopy type, and Bott periodicity 76
Homotopy type, and fibrations 18
Homotopy type, and Fredholm operators 293Ч294
Homotopy type, and Morse theory 196
Homotopy type, and spectral flow 296
Homotopy type, of 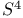 24 24
Hopf algebra 222
Hurewicz isomorphism 14
HuyghenТs principle 30
Hyperbolic equations 31
Hyperbolic monopoles see Monopoles
Hyperbolic plane 151 156
Hyperbolic space 247
Hyperbolic space, and hyperbolic monopoles 247Ч249
Hyperbolic space, and instanton moduli 241
Hyperk hler manifold 255 hler manifold 255
Hypo-elliptic operators 33
Hypo-ellipticity 32Ч35
Hypo-ellipticity, and supports of pseudo-differential operators 47
Index bundle 293Ч294
Index of elliptic operators 41 89Ч136
Index of elliptic operators, acting on functions 100Ч101
Index of elliptic operators, analytical see analytical index
Index of elliptic operators, and families of operators 118Ч122
Index of elliptic operators, and fixed point theory 122Ч127
Index of elliptic operators, and manifolds with boundary 127Ч136 288
Index of elliptic operators, and odd dimensional manifolds 98Ч99
Index of elliptic operators, and the Gauss Ч Bonnet theorem 104Ч106
Index of elliptic operators, and the Hirzebruch signature theorem 112
Index of elliptic operators, and the Lefschetz fixed point theorem 123Ч126
Index of elliptic operators, and the Riemann Ч Roch theorem 108
Index of elliptic operators, cohomological formula for 98 103 237
Index of elliptic operators, the 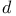 operator 103 117 operator 103 117
Index of elliptic operators, the 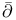 operator 106Ч108 117 operator 106Ч108 117
Index of elliptic operators, the Dirac operator 112Ч116 118 270
Index of elliptic operators, the signature operator 108Ч112 118
Index of elliptic operators, topological see Topological index
Index of elliptic operators, twisted operators 116Ч118
Index theorem of Atiyah and Singer 97
Inductive limit 71
Infinite dimensional groups 170Ч191
Infinite dimensional groups, the diffeomorphism group 174
Infinite dimensional groups, the group  171Ч174 171Ч174
Infinite dimensional groups, the group of gauge transformations 175Ч177
Infinite dimensional groups, the loop group 174Ч175
Infinite dimensional groups, the Virasoro group 174
Infinite dimensional manifolds 170Ч171 178 323
Instanton number 230
instantons 25Ч26 213Ч215 227Ч242 258
Instantons, and Donaldson invariants 332Ч339
Instantons, and Floer homology 327Ч330
Instantons, and Morse theory 213Ч215 258
Instantons, axially symmetric 246Ч250 253
Instantons, moduli space of 227Ч242
Instantons, time independent 245Ч246
Integrable system 173
Integral curve 159 174 212
Intersection form 23Ч25 108 240 338
Intersection number 143
Invariant polynomial 223 226
Inverse limit 19
Ising model 312Ч313
Isothermal coordinates 157
Isotopy 339Ч341
Jacobian variety 143
Jones polynomial 341Ч342
Jones polynomial, and Chern Ч Simons theory 343 350Ч359
K hler manifold 144Ч147 189 291 350 hler manifold 144Ч147 189 291 350
K hler metric 147 255Ч hler metric 147 255Ч
K-theory 11 65Ч75
K-theory, and anomalies 275
K-theory, and Bott periodicity 75Ч78
K-theory, and Fredholm operators 88 293Ч294
K-theory, and index theory 89Ч91 95Ч96 101Ч102 119-126
K-theory, and the Chern character 81
Kac Ч Moody algebra 173 177Ч178 180Ч183 187Ч188 311 317
Kac Ч Moody algebra, and current algebra 177 178
Kac Ч Moody algebra, Casimir operator for 181Ч183
Kac Ч Moody algebra, representations of 187Ч188
Kernel 40Ч41 46 54 69 89 92 122 132Ч133 162Ч165 176 179 230 236 252 276 281 292 297Ч298
Kernel, and Fock space 297Ч298
Kernel, and gauge transformations 176
Kernel, for a real elliptic family 122
Kernel, Gaussian 46
Kernel, of a group extension 179
Kernel, of an elliptic operator 89 92 122 132Ч133
Kernel, of Laplacians 40Ч41 92
Kernel, of the map  69 69
Knot invariants 339Ч340
Knot invariants, Alexander polynomial 340Ч342
Knot invariants, Homfly polynomial 341 360
Knot invariants, Jones polynomial 341Ч343 350Ч359
Knot invariants, knot group 340
Knots 2 338Ч360
| Knots, and Chern-Simons theory 342Ч360
Knots, and skein relation 342 351 353Ч355
Knots, mirror image of 341
Lagrange multiplier 347
Laplacian 27Ч28 39Ч41 46 92Ч93 127Ч128 148 163Ч164 209 236 260 282 332 349-350
Laplacian, and Hodge theory 92Ч93
Laplacian, and Ray Ч Singer torsion 349Ч350
Laplacian, on a K hler manifold 148 hler manifold 148
Laurent polynomial see 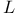 -polynomial -polynomial
Leading symbol 33Ч39 42 54 93 99Ч100 273
Lefschetz fixed point theorem 123Ч126
Level, curve 29 31
Level, of a representation 188 311 317 359
Level, set 29
Level, surface 195
Lexicographic ordering 291
Lie derivative 159Ч160 264
Lie group 9 11 73 75 125 170Ч171 174 178 180 185 188 190 192 201 207 221 226Ч227 241
Lie group, and instanton moduli 241
Lie group, and rational homotopy 221
Lie group, infinite dimensional 171Ч191
Light-cone 30
links 206 205 256 339 341Ч345 355Ч356
LiouvilleТs theorem 58
Local coefficients 21
Local cohomology 278 280
Locally convex 171
Loop group 173Ч174 181Ч183 191
Loop group, representations of 187Ч188
Lusternik Ч Schnirelmann category 198
M bius group 155 165 310Ч311 315 bius group 155 165 310Ч311 315
Magnetic charge 245 248Ч249 257
Magnetic monopole see Monopole
Mapping class group 152 155Ч156
Minima 25 229Ч230 244 256 258 336
Minima, and Yang Ч Mills action 25 229Ч230 258 336
Minima, and Yang Ч Mills Ч Higgs energy 244 256
Modular form 161 312
Modular functor 321
Modular group 155 161 170 317
Modular invariance 313 321
Modular transformation 155 311 359
Moduli space 26 139 152Ч165
Moduli space, instanton 26 227Ч242 333Ч339
Moduli space, monopole 250Ч256
Moduli space, of flat connections 350 360
Moduli space, Riemann 139 152Ч165 262 268 315
Moduli space, universal Riemann 318Ч319
Monopoles 242Ч250
Monopoles, and Morse theory 256Ч257
Monopoles, and rational functions 253
Monopoles, hyperbolic 246Ч250
Monopoles, moduli space of 250Ч256
Monopoles, Prasad Ч Sommerfield 243 252Ч253
Monopoles, scattering of 250 253Ч256
Morse theory 192Ч215
Morse theory, and Floer theory 322 324Ч326 330
Morse theory, and gauge theories 256Ч258
Morse theory, and the Morse inequalities 194Ч195 200 203 211Ч212 215
Morse theory, and the Morse series 193 197 199Ч200 203Ч205
Morse theory, equivariant 201Ч205
Morse theory, for critical sub-manifolds 199Ч201
Morse theory, via quantum mechanics 207Ч215
Multi-index notation 32
Neumann problem 128
Normal bundle 66 94 199
Nullity 193
Obstruction theory 21Ч23 26
Operator product expansion 301Ч310 314Ч315
Operator products 181
Orbifold 152 156
Parabolic equation 31 33Ч34
Parallel transport 216Ч218
Parametrix 55
Partition function 218 260Ч268 271 275
Partition function, and anomalies 271Ч275 278
Partition function, and axiomatic conformal field theory 318Ч321
Partition function, and Donaldson invariants 337
Partition function, and the Ising model 311 313
Partition function, for strings 260Ч268
Partition function, for the Chern-Simons action 343Ч351 357
Partition of unity 48 61
Path connected 11 14 218
Path ordering 343Ч344
Perfect Morse function 195
Period matrix 143Ч144
Peter Ч Weyl theorem 190
Pfaffian 86
Phase space 350
Phase transition 301
Picard group 146
Piecewise-linear manifold see PL manifold
PL manifold 2 20Ч22
Poincar conjecture 24 192 conjecture 24 192
Poincar duality 23 144 238 337 duality 23 144 238 337
Poincar polynomial 199 323 polynomial 199 323
Poincar polynomial, upper-half-plane 151 polynomial, upper-half-plane 151
Pointed space 5Ч6 9
Polyakov string formulation 259
Polygonal knot 340
Pontrjagin class 16 84Ч85 98 100Ч101 116 271
Positive line bundle 163Ч164 (see also Vanishing theorems)
Prasad-Sommerfield monopole 243 252Ч253
Primary field 302Ч317
Primary field, and knots 355Ч356
Principal bundle 15 33 175 219 281
Product metric 135
Projective connection 320
Projective limit 19
Projective representation 185Ч186
Pseudo-differential operators 41Ч44 89 91 94 131
Pseudo-differential operators, and Sobolev spaces 47Ч55
Pseudo-differential operators, on odd dimensional manifolds 99
Pseudo-locality 47
Quadratic differential 161Ч162
Quantised mass 227
Quaternionic projective space 323
Rank of a vector bundle 15 36 38 42Ч43 65 70Ч74 79Ч87 100 105 116 138Ч139 145Ч146 187 199 203 239 248 276
Rank of a vector bundle, and the stable range 72 74
Rank of a vector bundle, and virtual dimension 68Ч69
Rarita Ч Schwinger operator 289
Rational cohomology 81 98 121 123
Rational conformal field theory 313
Rational function 253
Real vector bundle see under Vector bundle
Reduced join 6
Reduced product 6
Renormalisation group 301
Representations 185Ч191
Representations, and Wilson lines 343
Representations, of the fundamental group 330
Representations, of the Kac-Moody algebra 187Ч188
Representations, of the Virasoro algebra 185Ч187 309Ч310
Riemann surface 1 10 133Ч134 139Ч144 147 148Ч169 197 257Ч268 302 316Ч322 350 358
Riemann surface, and Chern-Simons theory 350 358
Riemann surface, and conformal field theory 302 316Ч322 350 358
Riemann surface, and divisors 139Ч144
Riemann surface, and K hler manifolds 147 hler manifolds 147
Riemann surface, and moduli space 152Ч165
Riemann surface, and Morse theory 197
Riemann surface, and strings 259Ч268
Riemann surface, and Teichm ller space 148Ч151 ller space 148Ч151
Riemann surface, and the 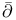 operator 133Ч134 operator 133Ч134
Riemann surface, and the Weierstrass gap theorem 166Ч169
Riemann surface, Yang-Mills theory on 257Ч258
Riemann uniformisation 150 152
Riemann Ч Roch theorem 98 108 168
Rigid rotation 183
Root space 190
Roots 190 290
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



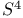
 hler manifold
hler manifold 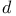 operator
operator 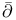 operator
operator 

 -polynomial
-polynomial bius group
bius group  conjecture
conjecture  ller space
ller space