|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Eisenhart L.P. — Riemannian geometry |
|
|
 |
| Предметный указатель |
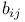 197 197
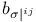 189 189
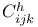 90 94 90 94
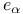 37 37
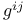 14 14
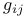 14 34 14 34
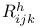 19 19
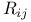 21 21
 84 84
 , applicable hypersurfaces 200 201 , applicable hypersurfaces 200 201
 , motions 87 192 , motions 87 192
 , n-tuply orthogonal systems in 121 , n-tuply orthogonal systems in 121
 , spaces conformal to an 91—93 121—124 182 214—218 , spaces conformal to an 91—93 121—124 182 214—218
 , sub-spaces 187—220 , sub-spaces 187—220
 1 1
 in a in a  , associate directions 74 75 167 , associate directions 74 75 167
 in a in a  , asymptotic directions 166 , asymptotic directions 166
 in a in a  , asymptotic lines 167 175 176 , asymptotic lines 167 175 176
 in a in a  , conjugate directious 166 167 175 176 , conjugate directious 166 167 175 176
 in a in a  , equations 44 , equations 44
 in a in a  , equations of Gauss and Codazzi 163 172 , equations of Gauss and Codazzi 163 172
 in a in a  , geodesics 75 , geodesics 75
 in a in a  , in an $S_{n+p} 195—197 , in an $S_{n+p} 195—197
 in a in a  , lines of curvature 168 , lines of curvature 168
 in a in a  , mean curvature 168 178 , mean curvature 168 178
 in a in a  , mean curvature normal 169 170 178 , mean curvature normal 169 170 178
 in a in a  , metric properties 45 48 , metric properties 45 48
 in a in a  , normal and relative curvatures of a curve 150—154 158 164 165 , normal and relative curvatures of a curve 150—154 158 164 165
 in a in a  , normals 41 47 140 143—146 158 , normals 41 47 140 143—146 158
 in a in a  , of constant curvature 210—214 , of constant curvature 210—214
 in a in a  , parallelism 74 75 167 , parallelism 74 75 167
 in a in a  , relative curvature 174 , relative curvature 174
 in a in a  , second fundamental form 166 , second fundamental form 166
 in a in a  , totally geodesic 183—186 249 , totally geodesic 183—186 249
 in an in an 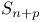 , equations 187 , equations 187
 in an in an 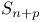 , equations of Gauss and Codazzi 190 197 198 , equations of Gauss and Codazzi 190 197 198
 in an in an 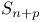 , evolutes 193 198 , evolutes 193 198
 in an in an 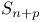 , lines of curvature 193 198 199 , lines of curvature 193 198 199
 in an in an 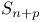 , motion 192 , motion 192
 in an in an 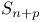 , principal radii of normal curvature 193 198 , principal radii of normal curvature 193 198
 , class 188 , class 188
 , conformal to an , conformal to an  91—95 121—124 182 214—218 91—95 121—124 182 214—218
 , curvature 80 81 83 113 157 159 , curvature 80 81 83 113 157 159
 , elemental 8 39 , elemental 8 39
 , evolutes 193 198 , evolutes 193 198
 , of class one 197—200 , of class one 197—200
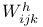 135 141 135 141
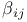 120 120
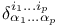 101 101
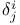 2 2
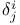 , components of a tensor 10 15 , components of a tensor 10 15
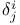 , contraction 13 , contraction 13
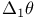 , , 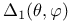 , , 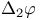 41 41
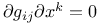 , along a curve 92 , along a curve 92
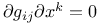 , at a point 55 56 , at a point 55 56
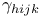 98 98
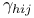 97 97
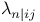 symmetric 115 symmetric 115
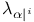 8 40 8 40
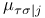 161 163 161 163
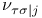 189 189
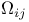 147 158 168 147 158 168
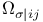 160 160
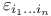 , , 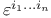 101 101
Abelian group 243 249
Angle, between hypersurfaces 41
Angle, between parametric curves 38
Angle, measure of 37 47
Applicable hypersurfaces, of a space of constant curvature 212
Applicable hypersurfaces, of an  200 201 200 201
Associate curvature of a vector 73 164
Associate curvature of a vector of orders 1,...,n-1 106
Associate directions of a vector 73-78
Associate directions of a vector, in a sub-space 74 75 167
Associate directions of a vector, of normals to a hypersurface 157
Associate directions of a vector, of orders 1,...,n-1 105
Associate tensor 16
Asymptotic, directions in a hypersurface 156
Asymptotic, in a  in a in a  166 167 166 167
Asymptotic, lines of a  in a in a  167 175 176 167 175 176
Asymptotic, lines of a hypersurface 156—158
Beltrami 134 219 252
Bianchi 21 59 60 73 75 77 79 82 88 94 121 150 154 158 159 179 200 206 210 213 218 219—222 224 225 227 236 239 242—244 246 247 249 253—255
Bianchi, identity of 82
Birkhoff 55 255
Blaschke 107 254
BLISS 49 256
Bocher 23 109 144 145 201 253
Bolza 49 253
Bompiani 167 170 175 179 184—186 254—256
Brinkmann 94 95 215 255 256
Bromwich 108 111 253
Cartesian coordinates 34
Cartesian coordinates, generalized 84 87 120 187
Christoffel 5 17 21 26 28 252
Christoffel symbols 17
Christoffel symbols, as components of a tensor 22
Christoffel symbols, in two coordinate systems 19
Class of a  188 188
Codazzi, equations of 149 150 162 172 190 198 211 212
Coefficients of rotation 97—100
Components, number 11
Components, of a tensor 9 10
Components, of a vector 4 7
Conformal, correspondence 89—91 182
Conformal, curvature tensor 91
Conformal, spaces 89—95 121—124 182 214—219
Conformal, transformations 230—233
Congruence of curves 6
Congruence of curves, canonical 125—128 139 140 154 241
Congruence of curves, geodesic 100 115 139 241
Congruence of curves, normal 114—125 128 140 142 154 185
Congruence of curves, normal to sub-spaces 41 47 140 144—146 158
Congruence of curves, principal 110 118
Conjugate directions, in a  in a in a  166 167 175 176 166 167 175 176
Conjugate directions, in a hypersurface 156
Conjugate tensor 15
Continuous group, Abelian 243 249
Continuous group, complete 244
Continuous group, conformal 230—233
Continuous group, constants of composition 224
Continuous group, generator 222
Continuous group, infinitesimal transformations 222
Continuous group, intransitive 225 233 235 236 244 249
Continuous group, invariant variety 225—227 235
Continuous group, minimum invariant variety 225 227 233 236 244 249
Continuous group, necessary and sufficient conditions 224
Continuous group, of one parameter 221
Continuous group, of r parameters 223
Continuous group, order of transformations of a 224
Continuous group, paths 222 231 235 239 240 241 249
Continuous group, simply transitive 247 249
Continuous group, sub-group of stability 225
Continuous group, transitive 225 236
Contraction 13
Contravariant, differentiation 31
Contravariant, tensor 9 10
Contravariant, vector 4 5 10 36 39
coordinates see “Cartesian”
Coordinates, geodesic 56
Coordinates, normal 55
Coordinates, of Weierstrass 204—210
Coordinates, polar 34
Coordinates, Riemannian 53—55
Coordinates, transformation of 1 8 23 25 55 141
Correspondence, conformal 89 182
Correspondence, geodesic 131—139 141 227—230
Correspondence, isometric 84—88 184
Covariant derivative 27—31
Covariant derivative, zero 28 29 107 124 141 142
| Covariant differentiation, 27—31
Covariant differentiation, of the inner product 29
Covariant differentiation, of the outer product 28
Covariant differentiation, of the sum or difference of tensors 28
Covariant tensor 9 10
Covariant vector 7 10
Covariant vector, geometrical interpretation 39
Covariant vector, null 36
Covariant vector, unit 36
Curl of a vector 27 31
Curvature of a  , invariant 83 157 , invariant 83 157
Curvature of a  , mean 113 , mean 113
Curvature of a  , Riemannian 79—81 113 159 , Riemannian 79—81 113 159
Curvature of a  , scalar 83 157 , scalar 83 157
Curvature of a curve 61
Curvature of a curve, (n-1) 107
Curvature of a curve, geodesic 152
Curvature of a curve, in a hypersurface 150—152
Curvature of a curve, normal 150—154 158 165 193
Curvature of a curve, relative 151 165
Curvature tensor see “Riemann tensor”
Curvature tensor, conformal 91
Curvature tensor, projective 135
Curvature, associate see “Associate curvature”
Curvature, lines of see “Lines of curvature”
Curvature, mean, of a  in a in a  168 178 168 178
Curvature, mean, of a hypersurface 168
Curvature, relative, of a  in a in a  174 174
Curve 6
Curve, curvature of 61 107
Curve, length 36 37
Curve, minimal 37
Curve, mutually orthogonal normals 107
Curve, of length zero 37
Curve, osculating geodesic surface 62
Curve, principal normal 61
Curve, tangent to 6
Curves, congruence of see “Congruence”
Curves, orthogonal to a hypersurface 43
Darboux 120 253
Deltas, Kronecker 2
Determinants 101—103
Di Pirro 131 252
Dienes 65 255
Differential forms see “Quadratic differential forms”
Differential parameters 41 47 124
Directions, associate see “Associate”
Directions, asymptotic see “Asymptotic”
Directions, conjugate see “Conjugate”
Directions, principal see “Principal”
Divergence, of a tensor 32
Divergence, of a vector 32 47
Dummy index 3
e 35 36
Eddington 69 101 255
Einstein 32 113 188 254
Einstein space 92 93 189 200
Einstein space, conformal to an  93 93
Einstein space, spaces conformal to an 94 95
Eisenhart 31 46 69 72 118 124 133 140 142 184 251 253—256
Element, of length 34 35
Element, of volume 177 179
Ennuple see “Orthogonal ennuple”
Equations, of Codazzi see “Codazzi”
Equations, of Euler see “Euler”
Equations, of Gauss see “Gauss”
Equations, of Killing see “Killing”
Euclidean space 34
Euclidean space, conformal representation of 94
Euclidean space, hypersurfaces 218
Euclidean space, motion 87 192
Euler, equations of 49 177
Euler, formula of 154
Evolutes of a  193 198 193 198
Fermi 92 255
First integrals of the equations of geodesics 128-131 138 141 238
Flat space 84
Formulas of Frenet 107
Fubini 231 233 236 237 244 246 253
Fundamental form 34 57
Fundamental form, second 150 155 156 166
Fundamental form, third 219
G 14
Gauss 45 57
Gauss, equations of 149 150 163 172 190 197 200
Gaussian curvature of a geodesic surface 81
Geodesic, congruences 100 115 139 241
Geodesic, coordinates 56
Geodesic, correspondence 131—139 141
Geodesic, curvature 152
Geodesic, form of the linear element 57
Geodesic, surface 79 81
Geodesic, surface osculating a curve 62
Geodesic, torsion 174
Geodesic, triangle 79
Geodesic, variety 166 167 176 183—186 249
Geodesically parallel hypersurfaces 57 158 249
Geodesics 49—52; see also “First integrals etc.”
Geodesics, as paths of a motion 239
Geodesics, characteristic property 64
Geodesics, equations in finite form 59
Geodesics, equations of 50—52 141
Geodesics, in a space of constant curvature 139 207—210 213 219 230
Geodesics, in Riemannian coordinates 53
Geodesics, infinitesimal transformations preserving 227—230
Geodesics, minimal 51 210
Geodesics, of a sub-space 75 156
Geodesics, spaces with corresponding 131—139 141
Goursat 1 5 42 58 70 252 253
Gradient 7 27
Group see “Continuous group”
Group of motions 233—251
Group of motions, intransitive 235 236 244 249
Group of motions, invariant varieties 235 245
Group of motions, minimum invariant varieties 236 244 249
Group of motions, of a regular space 250
Group of motions, of a space of constant curvature 207 238
Group of motions, order of transformations 238
Group of motions, paths 235 239 240 241 249
Group of motions, simply transitive 249
Group of motions, spaces 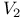 admitting a 241—244 admitting a 241—244
Group of motions, spaces 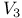 admitting a 245 admitting a 245
Group of motions, transitive 236 250 251
Group of motions, translations 239 241 249
hadamard 184 253
Herglotz 93 254
Homogeneous space 114
Hypercone, fundamental 215
Hyperquadric, fundamental 202 203
Hypersphere 202
Hypersurface, conjugate and asymptotic directions 156
Hypersurface, curvature of a curve in a 150—152
Hypersurface, curves orthogonal to a 43
Hypersurface, definition 8 41
Hypersurface, equations of Gauss and Codazzi 149 150 197
Hypersurface, geodesics 75 156
Hypersurface, isothermic 116 241
Hypersurface, lines of curvature 153—157 159 213 219
Hypersurface, mean curvature 168
Hypersurface, minimal 178
Hypersurface, normals parallel along a curve 158
Hypersurface, normals to a 41
Hypersurface, null normals to a 41
Hypersurface, of a flat space 197—201 218 219
Hypersurface, of a space of constant curvature 157 159 212 213 218—220
Hypersurface, principal radii of normal curvature 153 158
Hypersurface, relative and normal curvatures 151
Hypersurface, second fundamental form 150 155 156
Hypersurface, third fundamental form 219
Hypersurface, totally geodesic 183 184 249
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



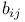
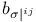
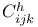
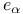
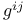
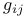
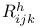
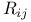


 , associate directions
, associate directions 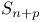 , equations
, equations 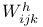
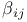
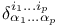
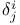
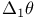 ,
, 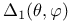 ,
, 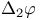
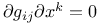 , along a curve
, along a curve 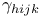
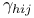
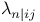 symmetric
symmetric 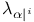
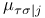
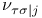
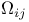
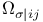
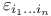 ,
, 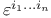
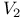 admitting a
admitting a 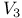 admitting a
admitting a