|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Eisenhart L.P. — Riemannian geometry |
|
|
 |
| Предметный указатель |
Hypersurface, with indeterminate lines of curvature 179—183 185 218 249
Hypersurfaces see “N-tuply orthogonal systems”
Hypersurfaces, angle between 41
Hypersurfaces, applicable 200 201 212
Hypersurfaces, geodesically parallel 57 158 249
Hypersurfaces, orthogonal 42
Identities of Ricci 30
Identity of Bianchi 82
Indeterminate lines of curvature 179—183 185 218 249
Infinitesimal motion 234 235 237
Infinitesimal transformation of a group 222 223
Infinitesimal transformation of a group, conformal 230—233
Infinitesimal transformation of a group, contravariant components 223
Infinitesimal transformation of a group, linearly independent 223
Infinitesimal transformation of a group, order 224
Infinitesimal transformation of a group, symbol of 222
Infinitesimal transformation of a group, which preserve geodesics 227—230
Infinitesimal translation 239 249
Inner multiplication 13 29
Intransitive group 225 233 235 236 244 249
Intrinsic, derivative 98
Intrinsic, property 84 192
Invariant 6 97 124
Invariant, covariant derivatives 27 29
Invariant, curvature of a  83 157 83 157
Invariant, principal 110 124
Isometric, correspondence of spaces 84—88 184
Isometric, spaces 84
Isothermic hypersurfaces 116 241
Kasner 189 200 255
Killing 200 234 252
Killing, equations of 234 237
Kommerell 184 253
Kottler 93 254
Kowalewski 103 104 253
Kronecker delta 2
lame 116 252
Length, element of 34 35
Length, of a curve 36 37
Levi-Civita 5 13 21 30 31 64 65 69 74 79 83 92 97 100 107 116 117 124 125 127 131 136 138 241 252—254 256
Levy 33 59 94 140 141 218 256
Lie 221 222 224 252
Line, asymptotic see “Asymptotic”
Lines of curvature, indeterminate 179—183 185 218 249
Lines of curvature, of a  in a in a  168 168
Lines of curvature, of a  in an in an 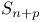 193 198 193 198
Lines of curvature, of a hypersurface 153—159 199 213 219
Lipschitz 177 178 252
M 169
Matrices 101—103
Mean curvature normal 169 170 178 185
Mean curvature, of a  for a direction 113 for a direction 113
Mean curvature, of a hypersurface 168
Mean curvature, of a sub-space 168 178
Metric of a space 34 35
Meusnier's theorem, generalization of 152
Minimal, curve 37
Minimal, geodesic 51 210
Minimal, surface 177 184
Minimal, variety 177—179 184 186
Motion see “Group of motions”
Motion, in a space 87 88
Motion, infinitesimal 234 235 237 239 249
Motion, of a space of constant curvature into itself 204 207 238
Motion, of an  into itself 192 into itself 192
Motion, paths of 235 239 240 241 249
Murnaghan 102 107 256
N-tuply orthogonal systems of hypersurfaces 43 44 117—124 138 155 158 220
Normal, congruences see “Congruences”
Normal, coordinates 55
Normal, curvature of a curve in a subspace 150—154 158 165 193
Normal, mean curvature 169 170 178 185
Normal, null 41
Normal, principal, to a curve 61 107
Normal, to a  in a in a  47 140 143—146 192 47 140 143—146 192
Normal, to a hypersurface 41 158
Null vector 36 38 41 111 112
Order, of a tensor 9 10
Order, of an infinitesimal transformation 224
Orthogonal ennuples 40
Orthogonal ennuples, canonical 125—128 139 140 154 241
Orthogonal ennuples, determination of tensors 97
Orthogonal ennuples, number of 40
Orthogonal ennuples, of normal congruences 117—119 128 140
Orthogonal ennuples, of Schmidt 103 104
Orthogonal systems of hypersurfaces see “N-tuply orthogonal etc.”
Osculating, geodesic surface of a curve 62
Osculating, geodesic variety 167 176 185 186
Outer product 12 29
Parallel displacement of a vector 65—67 79 93 184
Parallel vectors, fields of 67—72 142 185 239
Parallelism of vectors 64
Parallelism of vectors, in a sub-space 74 75 167
Parallelism of vectors, in a totally geodesic sub-space 184
Parallelism of vectors, normal to a hypersurface 158
Parallelism of vectors, tangent to a 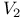 79 175 79 175
Parallelism of vectors, tangent to a sphere 76
Paths of a continuous group 222 231 235 239 240 241 249
Peres 65 79 93 254
Point 1
Point, umbilical 179 185
Poisson operator 70
Principal, congruences 110 118
Principal, directions 107—114 124 181 199 219
Principal, invariants 110 124
Principal, normal to a curve 61 107
Principal, radii of normal curvature 153 158 193
Projective, curvature tensor 135
Projective, plane space 135
Quadratic differential form 22
Quadratic differential form, equivalence 23—26 86—88
Quadratic differential form, fundamental 34
Quadratic differential form, Liouville form 60
Quadratic differential form, of constant curvature 25 85 93 206 218 219
Quadratic differential form, positive definite 23
Quadratic differential form, second and third of a hypersurface 150 155 156 219
Quadratic differential form, signature 23
Quadratic differential form, transformation 24 86
R 22 83
Radius of, curvature of a curve 61 107
Radius of, normal curvature 150—154 158 165 193
Regular space 250
Relative, curvature see “Curvature of a curve”
Relative, tensor 31
Relativity 34 37 51 83 113 140 188 189
| Ricci 5 13 21 22 30 31 97 107 113 116 117 124 125 127 139 140 159 163 172 174 181 183 184 188 190 241 250—253 256
Ricci, identities 30
Ricci, principal directions 114 181 199 219
Ricci, tensor 22 32 47 92 93 113 114 135 200
Riemann 34 53 80 86 252
Riemann, symbols 20 21
Riemann, tensor 20 25 30 32 33 44 47 81—84 93 159 162 172 180 187 211 212 237
Riemannian, coordinates 53—55
Riemannian, curvature 79—81 113 159
Riemannian, form of the linear element 86
Riemannian, geometry 35
Riemannian, metric 35
Riemannian, space 35
Rotation, coefficients of 97—100
Rotation, in an  192 192
Sbrana 201 253
scalar 6
Scalar, curvature of a space 83 157
Schmidt 104 253
Schouten 16 22 65 92 93 124 125 134 182 185 199 200 254 255
schur 83 252
Schwarzschild 93 188 254
Severi 64 254
Signature of a quadratic differential form 23
Six-vector 12
Sommerville 254
Space see “Einstein space”
Space of constant Riemannian curvature 83
Space of constant Riemannian curvature, applicable hypersurfaces 212
Space of constant Riemannian curvature, fundamental form 25 85 93 206 218 219
Space of constant Riemannian curvature, geodesic correspondence 134
Space of constant Riemannian curvature, geodesics 134 139 207—210 213 219 230
Space of constant Riemannian curvature, hypersurface 157 159 212 213 218—220
Space of constant Riemannian curvature, infinitesimal transformations 230 232
Space of constant Riemannian curvature, isometric correspondence 84
Space of constant Riemannian curvature, linear first integrals of the equations of geodesics 239
Space of constant Riemannian curvature, motions 86—88 204 207 238
Space of constant Riemannian curvature, n-tuply orthogonal systems 220
Space of constant Riemannian curvature, spaces conformal to 91 219
Space of constant Riemannian curvature, sub-spaces 212
Space, flat see “Flat and  ” ”
Space, homogeneous 114
Space, metric 34
Space, n-dimensional 1
Space, projective plane 135
Space, regular 250
Space, Riemannian 35
Space-time continuum of a perfect fluid 140
Spaces, applicable 75 84 200 201 212
Spaces, conformal 89
Spaces, conformal to an  91—93 121—124 182 214—218 91—93 121—124 182 214—218
Spaces, conformal to an Einstein space 93—95
Spaces, tangent 75
Spaces, with corresponding geodesics 131—139 141
Staeckel 130 140 252
Struik 92 93 134 181 185 186 188 199 200 249 254 255
Sub-group of stability 225
Surface, geodesic 62 79 81
Surface, minimal 177 184
Surface, of translation 175 184
Synge 65 255
Tangent, sub-spaces 75
Tangent, to a curve 6
Tensor see “Riemann tensor”
Tensor density 31
Tensor, see “Ricci tensor”
Tensor, associate 16
Tensor, conformal curvature 91
Tensor, conjugate 15
Tensor, contraction 13
Tensor, contravariant 9 10
Tensor, covariant 9 10
Tensor, divergence 32
Tensor, fundamental 35
Tensor, mixed 9 10
Tensor, order 9 10
Tensor, rank 16
Tensor, relative 31
Tensor, satisfying equations (8.10) and (8.11) 32 48
Tensor, skew-symmetric 11
Tensor, symmetric 11
Tensor, whose first covariant derivative is zero 28 29 107 124 141 142
Tensor, zero 11
Tensors, addition, subtraction, multiplication of 12
Tensors, composition 13
Tensors, inner product 13 29
Tensors, outer product 12 29
Tensors, quotient law 14
Thomas, J.M. 94 141 256
Thomas, T.Y. 69 141 255 256
Totally geodesic sub-space 183—186 249
Transformations of coordinates 1 23—25 55 141
Transformations of coordinates, conformal 230—233
Transformations of coordinates, linear 8 55
Transformations of coordinates, linear fractional 141
Transformations of coordinates, of a group 221 223
Transitive group 225 236 247 249—251
Translation 72 192 239 241 249
Translation, surface of 175 184
Umbilical point 179 185
Veblen 69 133 141 255 256
Vector, associate curvature 73 106 164
Vector, associate direction 73—78 105 157 167
Vector, contravariant 4 5 10 39
Vector, covariant 7 10 39
Vector, divergence 32 47
Vector, magnitude 35
Vector, normal curvature 165
Vector, null 36 38 41 111 112
Vector, parallel displacement 65—67 79 93 184
Vector, relative curvature 151 165
Vector, unit 36 40
Vector-field 5 36;
Vectors see “Orthogonal ennuple”
Vectors, angle of 37 38
Vectors, n mutually orthogonal 40
Vectors, orthogonality 38
Vectors, parallelism see “Parallelism and Parallel vectors”
Verjuengung 13
Volume, element of 177 179
Voss 150 154 163 166 252
Weierstrass, coordinates of 204—210
Weight of a relative tensor 31
Weyl 65 91 92 133 135 254
Wilson 1 254
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





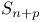
 into itself
into itself