|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Eisenhart L.P. — An introduction to differential geometry with use of the tensor calculus |
|
|
 |
| Предметный указатель |
 12. 12.
 , , 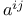 , a 70 72 , a 70 72
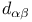 , ,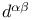 215 216 221 234 262 215 216 221 234 262
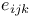 , , 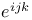 6 93 94 6 93 94
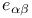 , , 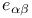 134 138 134 138
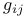 , , 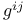 101 101
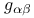 , , 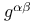 123 125 137 151 262 123 125 137 151 262
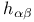 , , 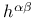 253 256 253 256
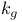 187 245 187 245
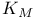 225 225
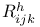 , , 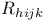 100—103 150 151 207 100—103 150 151 207
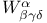 211 211
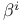 18 18
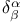 125 125
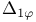 , , 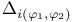 , , 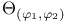 155 156 159 160 155 156 159 160
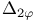 158 159 158 159
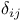 , ,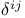 , , 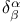 8 25 32 8 25 32
 , , 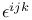 94 97 94 97
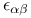 , , 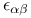 135 137 138 151. 135 137 138 151.
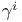 20 20
 16 16
 22 22
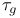 247 247
Angle, of curves in a surface 130—132 137 145
Angle, of curves in a surface, of vectors 133
Applicable surfaces 215; see Isometric surfaces
Arc of a curve 9
Area, element of 136
Area, minimum 290
Associate, minimal surface 293
Associate, vector 194 250 252
Asymptotic directions 237 241
Asymptotic lines 237—239 243
Asymptotic lines geodesic 248
Asymptotic lines orthogonal 238
Asymptotic lines straight 237 267
Asymptotic lines, coordinate 237 238 242 260 266
Asymptotic lines, osculating plane of 237
Asymptotic lines, plane 249
Asymptotic lines, spherical representation of 260 266 267
Asymptotic lines, tangential coordinates 264 265
Beltrami 158 189 208 275
Bertrand curves 30
Bianchi 194
Bianchi identities 121
Binormal of a curve 19
Bonnet 190 273
Calculus of variations 290
Carenold 128 242 294
Center of curvature, of a curve 18
Center of curvature, of a curve in a surface 227
Center of curvature, principal, of a surface 226
Characteristics of a family of surfaces 54
Christoffel symbols, as components of a tensor 100 102 103
Christoffel symbols, for a surface 149 153 154
Christoffel symbols, for space 98 102 121
Christoffel symbols, relations between for a surface and its spherical representation 257 260
Circle, of curvature 18
Circle, osculating 19
Circle, superosculating 24
Circles, orthogonal system, on the sphere 267
Codazzi equations 219 230 236 238
Combeseure transformation of curves 29
Complementary surfaces 275
Cone 53 57
Conformal correspondence, of a plane with itself 204
Conformal correspondence, of a sphere with itself 204
Conformal correspondence, of a sphere with the plane 204
Conformal correspondence, of a surface and its spherical representation 255
Conformal correspondence, of a surface of constant curvature with the plane 288
Conformal correspondence, of a surface with itself 203
Conformal correspondence, of two surfaces 201—205
Congruence of curves 78
Conjugate directions 231 241
Conjugate net 232 243
Conjugate net, coordinate 232 235 236
Conjugate net, isometric- 235 236
Conjugate net, mean- 240 243 260.
Conjugate net, of plane curves 266
Conjugate net, orthogonal 232
Conjugate net, spherical representation 260
Conjugate net, tangential coordinates 263
Conjugate systems in correspondence 243
Conoid, right 50 53 129 149 221 266
Contraction of indices 95
Contravariant, components 85 88 127 134
Contravariant, index 89
Contravariant, tensor 89 90 91
Contravariant, vector 77 82 126
Coordinate curves, in a surface 46 127
Coordinate curves, in space 69
Coordinate net 49
Coordinate surface 68 81
Coordinates cartesian 63 70 88
Coordinates cylindrical 83; see Polar coordinates Tangential
Coordinates, 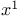 , , 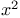 as 137 221 as 137 221
Coordinates, in a surface 48
Coordinates, in space 63—68
Covariant components 85 86 88 127 134
Covariant differentiation 107—112
Covariant differentiation, of 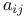 , , 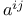 , , 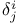 110 110
Covariant differentiation, of 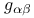 , , 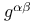 , , 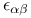 , , 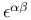 151 151
Covariant differentiation, of sum, difference, outer and inner product of tensors 111
Covariant index 89
Covariant tensor 89 90 91
Covariant vector 84 127
Cubic, twisted 5 7 8 16 44
Curvature normal, center of 224
Curvature normal, of a surface 224
Curvature normal, principal centers of 226
Curvature normal, principal radii of 225
Curvature normal, radius of 224 227
Curvature of a curve 16
Curvature of a curve, center of 18
Curvature of a curve, circle of 18
Curvature of a curve, constant 19 23 24 28
Curvature of a curve, first 22
Curvature of a curve, geodesic see Geodesic curvature
Curvature of a curve, of a triangle 183
Curvature of a curve, radius of 16
Curvature of a curve, second 22
Curvature of a surface, total 151; see Gaussian curvature Mean
Curvature tensor see Riemann tensor
Curvature, of a quadratic form 151
Curve twisted or skew 4
Curve, arc of 9
Curve, definition 3
Curve, form of 26
Curve, length of 9
Curve, minimal, or of length zero 10
Curve, of constant curvature 19 24 28
Curve, of constant torsion 24 28 29 30
Curve, plane 4
Curvilinear coordinates 47 69
Cylinder 3 53 61
D, D’, D’’ 216
Darboux 115 173 233
Developable surface 54 57—61 152
Developable surface, edge of regression 61
Developable surface, Gaussian curvature 150
Developable surface, geodesic in a 178
Developable surface, isometric with a plane 147
Developable surface, isotropic 61
Developable surface, lines of curvature 229
Developable surface, of normals to a surface 229
Developable surface, polar 61 149
Developable surface, rectifying 61
Developable surface, tangent planes 147 148
Developable surface, tangent surface of a curve 57
Differential parameters, of the first order 155 156 159 160
| Differential parameters, of the second order 158 159
Dini 210
Dini, surface of 287
Direction cosines of principal normal 18
Direction cosines of tangent 12
Direction cosines, of binormal 20 23
Divergence of a vector 113 155
Dupin indicatrix of a surface 241
E, F, G 126
Edge of regression 56 61
Element linear see Linear Element
Element, of area see Area
Ellipsoid 50; see Quadries central
Elliptic point of a surface 242
Enneper 248 292
Enneper, minimal surface of 294
Envelope, edge of regression 56 62
Envelope, of a family of spheres 62
Envelope, of a one-parameter family of surfaces 54—56
Envelope, of a oneparameter family of planes 57 see
Envelope, of characteristics 56
Equations parametric, of a line 1
Equations, parametric, of a curve 3
Equations, parametric, of a surface 46
Equivalent representation of surfaces 205
Euler, equation of 240
Euler, equations of 177 289
Evolute of a curve 36 38
Family characteristic 54
Family of curves in a surface 138—141
Family of geodesics 174
Family of planes 57
Family of spheres 62
Family, one-parameter, of surfaces 54
Formula of Green 190 192
Formula of Liouville 193
Frenet formulas 25 27
Frenet formulas in a surface 199
Frenet formulas in general coordinates 106
Fundamental quadratic form, first, of a surface 124
Fundamental quadratic form, of space 70
Fundamental quadratic form, second, of a starface 215
Fundamental tensor, first, of a surface 125 262
Fundamental tensor, of space 91
Fundamental tensor, second, of a surface 215 262
G 101 125
Gauss 45 151 174 184 216 219 225 252 254
Gauss — Bonnet theorem 191
Gauss, equation of 219
Gauss, equations of 216
Gaussian curvature of a surface 151 154 193 225 255
Generator of a developable surface 59
Generator of a surface of translation 236
Geodesic correspondence of two surfaces 205—211
Geodesic correspondence of two surfaces, of constant curvature 209
Geodesic curvature 186 193 199 201 243
Geodesic curvature, center of 246 275
Geodesic curvature, curves of constant 192 267
Geodesic curvature, radius of 276
Geodesic parallels 174 200
Geodesic polar coordinates 180—182
Geodesic torsion 247—249
Geodesic triangle 183 184 200
Geodesic, circles 180 186
Geodesic, ellipses and hyperbolas 185 186
Geodesics 170—179 187 246
Geodesics coordinate 173
Geodesics plane 248
Geodesics, equations of 171 179 197
Geodesics, in a surface of Liouville 176
Gradient 84
Group property 68
H 253
Helicoid, skew 129 145 165 242 294
Helieoid 53 129 218
Helieoid minimal 294
Helieoid pseudospherical 287
Helieoid spherical 287
Helieoid, isometric with a surface of revolution 160
Helieoid, parameter of a 129
Helieoid, surfaces of center 276
Helix circular 14 16 19 23 30 34 37
Helix conical 15
Helix cylindrical 15 19 24 28 37 38 149 178
Hyperbolic point of a surface 242
Hyperboloid 50 242
Hyperboloid, rulings 242; see Quadries central
Index , dummy 2
Index contravariant 89
Index covariant 89
Index free 2
Index lowering 95
Index raising 95
Indicatrix of binormal 22
Indicatrix of Dupin see Dupin
Indicatrix spherical, of tangent 17
Inner product of tensors 95
Intrinsic derivative 195
Intrinsic equations of a curve 31 147
Intrinsic geometry of a surface 146
inversion 233 236
Inversion, preserves lines of curvature 233
Involute of a curve 35 37 39
Isometric surfaces 147 150 166—169 171 197
Isometric, orthogonal net 161—165
Isometric, orthogonal net, -conjugate net 235 236
Isometric, orthogonal net, coordinates 161
K 151 154 193 225
Kronecker deltas 25 63
Lagrange 290
lame 158
Lelieuvre, formulas of 266
Levi-Civita 196 199 251
Line of curvature 228 229
Line of curvature, conjugate 232 233
Line of curvature, coordinate 230
Line of curvature, equation 228 277
Line of curvature, geodesic 248
Line of curvature, geodesic torsion of 248
Line of curvature, normal curvature of 229
Line of curvature, osculating plane of 259
Line of curvature, plane 230 249 260 266 268 276
Line of curvature, spherical 249
Line of curvature, spherical representation of 255
Line of curvature, two surfaces intersecting in a 248
Line of curvature, under an inversion 233
Linear element of a curve 9
Linear element of a surface 124
Linear element of space 70
Linear element of the spherical representation 252
Linearly independent (constant coefficients) 262
Lines of length zero see Minimal lines
Lines of shortest length 175
Liouville, formula of 193
Liouville, surface of 176
Loxodromic curve 145
Mainardi 219
McConnell 194
Mean curvature of a surface 225
Mean-conjugate net 240 243 260
Meridian of a surface of involution 49
Metric tensor, of a surface 124 125
Metric tensor, of space 91
Meusnier, theorem of 224
Minimal curve 10 16
Minimal curve on a sphere 154
Minimal curve on a surface 124
Minimal surface 238 249 288—295
Minimal surface adjoint 293
Minimal surface algebraic 293
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



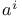
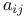 ,
, 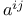 , a
, a 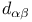 ,
,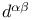
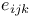 ,
, 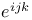
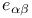 ,
, 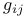 ,
, 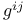
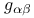 ,
, 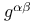
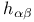 ,
, 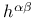
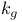
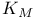
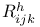 ,
, 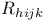
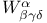
 ,
,  ,
, 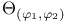
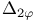
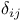 ,
,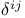 ,
, 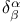
 ,
, 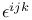
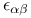 ,
, 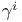


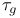
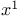 ,
, 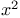 as
as