|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Elliot P.D.T.A. — Probabilistic Number Theory Two: Central Limit Theorems |
|
|
 |
| Предметный указатель |
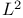 -norm 12 23 -norm 12 23
 -module 289 340 -module 289 340
Abel 352 239 243
Abel’s lemma 239 243
Abundant numbers 3 4 189
Acz l 76 l 76
Additive function, finitely distributed 11 259 260 267 270 275 275 283
Additive function, finitely distributed (definition) 258
Adjoint of operator 181 182
Akilov and Kantorovich 181
Algebra of sets 29 30 115 146
Analytic characteristic functions 57 112
Asymptotic density 98 100 109
asymptotic relations 19 21
Axer 239 240 241 243 244 261
Axer’s lemma 239 240 241 243 242 261
Babu 288 330
Bakstys 280
Banach — Hahn 181
Barban 9 12 80 92 93 136 184 27 40 41 44 50 51 263 268 269 329
Barban and A.I. Vinogradov 122 126 263
Barban — Vinogradov — Bombieri 51 269
Barban, Vinogradov and Levin 174 27 50
Basis 294
Bateman 261
Behrend 4 189 214
bernoulli 36
Berry 74 78 22
Berry — Esseen 74 101 117 217 22 266 269
Berry — Esseen theorem 74 117 22 265 269
Bertrand 3
Bessel — Hagen 3 4 189
Billingsley 30 288
Birch 14 98 99 120
Bohr H., address to 1950
Bohr, H. 248
Bombieri 12 90 92 93 184 185 186 317 261
Bombieri and Davenport 185
Bombieri — Barban — Vinogradov 51 269
Borel 3 170
Borel — Cantelli 45 46
Borel — Cantelli lemma, applications 45 46
Borel — Carath odory 58 odory 58
Borel — Carath odory lemma 58 odory lemma 58
Borel — Heine 168
Brownian motion 3 288
Brun 4 9 80 134 184 210 213 21 24 25 44
Brun — Titchmarsh 90 120 135 160 161 213 32
Brun’s Sieve 4 9 80 129 21 25 44
Burgess 154 157 339
Cantelli — Borel 45 46
Carath odory — Borel 58 odory — Borel 58
Cartwright 94
Cauchy 7 14 17 20 46 76 231 239 283 289 290 329 10 13 136 137 143 144 179 192 228 293 297 340 341
Cauchy law 14 136 143
Cauchy — Schwarz 42 68 135 149 150 151 160 161 164 168 174 196 197 201 202 234 243 246 271 300 304 317 338 339 345 348 349 28 42 43 57 117 220 259 278 283
Cauchy’s functional equation 17 20 76 283 289 179 340
Central limit theorem 218 18 24
Character, Dirichlet 110 — 111 178 222 241 313 338 339
Character, primitive 110 320
Characteristic exponent of stable law 135 142
Characteristic function 9
Characteristic function, (definition) 27
Characteristic function, analytic 57 112
Characteristic function, component of 113 114
Characteristic function, convergence of 28
Chowla and Erd s 314 329 s 314 329
Chowla, S. 4 189
Circle method 2 6
Class  , additive functions 12 14 17 27 29 30 38 53 125 336 , additive functions 12 14 17 27 29 30 38 53 125 336
Class  of Khinchine 125 167 169 of Khinchine 125 167 169
Class  , laws 148 161 164 173 337 , laws 148 161 164 173 337
Class Number, quadratic 14 110 117 313
Classification 13
Coefficients, Fourier 66
Compactness lemma 25
Component of characteristic function 113 — 114
Component of distribution function 113 168
Concentration function 31 217 218
Conditional probability 31 35
Congress Math 248
conjugate 12 181
Continued fraction, periodic 138
Continuity criterion, L vy’s 46 78 vy’s 46 78
Continuity of distribution function 48 49
Control, mathematical 13
Convergence, (definition) 273 — 274 280
Convergence, characteristic functions 28
Convergence, Fourier coefficients 67 68
Convergence, Mellin — Stieltjes transforms 63
Convergence, modified-weak 63
Convergence, weak 24 30
Convolution 30 254 255
Convolutions, infinite 37
Copenhagen lecture 248
Courant — Fisher 163
Courant — Fisher theorem 163 164
Cyclotomic field 114
Daboussi and Delange 358
Davenport 4 111 189 214 24 320
Davenport and Bombieri 185
Davenport and Halbertstam 12 185
de Bruijn 77
de Bruijn, van Aardenne — Ehrenfest and Korevaar 18 77
de la Vall e Poussin 1 29 261 e Poussin 1 29 261
Decomposition 13
Decomposition of 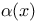 58 59 60 86 58 59 60 86
Dedekind 114
Dedekind — Dirichlet series 114
Delange 10 11 218 219 225 226 254 256 258 283 285 286 301 305 333 51 255 287 311 333
Delange and Daboussi 358
Density, asymptotic 98 100 109
Density, lower = density, lower asymptotic 295 297
Density, Schnirelmann 77 293
Desargues 12
Desargues’ theorem 12
diamond 219
Diamond and Steinig 261
Differences 16
Differential equation, approximate 13 75 80
Dirichlet 10 12 14 15 79 92 94 96 98 100 101 108 109 110 111 112 114 183 184 186 222 224 225 235 301 308 311 317 322 326 331 335 337 341 342 348 356 51 71 83 125 139 178 187 211 218 221 222 230 240 241 242 243 245 246 260 277 286 301 313 324 339
Dirichlet 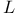 -series 14 110 111 114 241 313 -series 14 110 111 114 241 313
Dirichlet character 178 222 241 313 338 339
Dirichlet multiplication, convolution 98 109 277 301
Dirichlet, marriage of 111 112
Dirichlet-series 79 94
Dirichlet-series component 114
Dirichlet-series operator 186
Discriminant, fundamental 111 319
Discriminant, of quadratic field 110 111 313
Dispersion method 93 40
Distribution function 24
Distribution function, continuity of 48 49
Distribution function, convergence 24 25
Distribution function, improper 25
Distribution function, proper 25
Distribution functions (mod1) 65
Distribution functions (mod1) convergence 65 68
Distribution functions (mod1) discontinuous, quantitative Fourier inversion 75 76
Distribution functions (mod1), continuity of 67
Distribution law 24
Doeblin 2 7
Dual 12 13
Dual of operator 72 181
Dual of Tur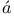 n — Kubilius inequality 13 147 194 335 55 114 n — Kubilius inequality 13 147 194 335 55 114
Dual space 181 182
Duality principle 150 162 185 316 315
Edwards 68
Egoroff 18 91
Einstein 3
| Elliott 12 13 75 76 144 153 155 185 217 218 219 269 283 286 292 295 333 8 37 48 52 58 60 93 99 101 103 110 112 120 122 123 125 147 148 180 184 208 209 247 286 289 314 328 329 331 334 338
Elliott and Halberstam 272
Elliott and Ryavec 10 257 258 265 268 283 306 169
Eratosthenes 221 254 266
Erd s 3 4 5 10 11 90 91 118 187 189 203 207 210 211 212 213 214 218 219 220 254 258 265 283 285 301 302 18 19 20 21 23 24 25 26 99 119 120 202 203 205 206 207 248 249 250 253 329 330 331 332 335 s 3 4 5 10 11 90 91 118 187 189 203 207 210 211 212 213 214 218 219 220 254 258 265 283 285 301 302 18 19 20 21 23 24 25 26 99 119 120 202 203 205 206 207 248 249 250 253 329 330 331 332 335
Erd s and Chowla 314 329 s and Chowla 314 329
Erd s and Kac 4 5 14 146 182 214 12 18 20 24 25 26 262 302 s and Kac 4 5 14 146 182 214 12 18 20 24 25 26 262 302
Erd s and R s and R nyi 333 nyi 333
Erd s and Ryavec 268 s and Ryavec 268
Erd s and Selberg 10 256 211 248 258 s and Selberg 10 256 211 248 258
Erd s and Selberg, elementary proof of P.N.T. 248 — 253 s and Selberg, elementary proof of P.N.T. 248 — 253
Erd s and Tur s and Tur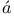 n 75 n 75
Erd s and Tur s and Tur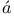 n inequality 75 n inequality 75
Erd s and Wintner 4 10 187 214 254 280 24 172 260 332 335 s and Wintner 4 10 187 214 254 280 24 172 260 332 335
Erd s at Kac’ lecture 24 25 s at Kac’ lecture 24 25
Erd s — Kac theorem 18 262 s — Kac theorem 18 262
Erd s — Kac — Kubilius 9 31 48 125 s — Kac — Kubilius 9 31 48 125
Erd s — Wintner theorem 187 224 s — Wintner theorem 187 224
Erd s, Ruzsa and S s, Ruzsa and S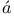 rk rk zy 290 296 zy 290 296
Erd s’ sample paper 207 210 s’ sample paper 207 210
Erd s’ sample paper, commentary on 210 213 s’ sample paper, commentary on 210 213
Esseen 74 78 203 218 22 274 283 327
Esseen — Berry 74 101 117 217 22 266 269
Esseen — Berry theorem 74 117 22 266 269
Esseen’s inequality 74
Euclid 4
Euler 89 95 96 97 114 134 188 203 230 326 338 341 349 353 76 79 80 82 84 196 277 287 301 314 320 339
Euler product 95 97 114 230 326 338 341 349 353 76 79 80 82 84 196 277 301 314 320 339
Euler’s constant 89
Euler’s function, distribution of 188 — 189 213 214
Fa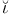 nle nle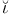 b 74 75 203 219 b 74 75 203 219
Fa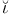 nle nle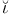 b and Levin 11 286 145 b and Levin 11 286 145
Fa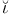 nle nle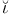 b and Toleuov 46 51 b and Toleuov 46 51
Fej r 3 70 78 101 229 r 3 70 78 101 229
Fej r kernel 78 101 229 r kernel 78 101 229
Feller — Lindeberg 56 17
Feller — Lindeberg condition 56 17
Field 248
Finite probability space 5 115 146 323
Finitely distributed additive function 77 259 260 267 270 275 276 283
Finitely distributed additive function (definition) 258
Finitely monotonic additive function 268 269
Fisher — Courant 163
Fisher — Courant theorem 163 164
Forti and Viola 12 185 186 317
FOURIER 71 74 77 196 199 219 222 223 227 274 327
Fourier coefficients 66
Fourier inversion (mod 1) quantitative 74 76
Fourier inversion, quantitative 69
Fourier — Stieltjes 61 305
Fourier — Stieltjes transform 61 (see also Characteristic Function)
Fr chet — Shohat 59 78 chet — Shohat 59 78
Fr chet — Shohat — Wintner 59 60 78 chet — Shohat — Wintner 59 60 78
Fubini 68
Functional equation, approximate for 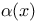 61 61
Functional equation, Cauchy’s 17 20 76 283 289 179 340
Functions, slowly oscillating 18
Fundamental lemma 80 25 26
Galambos 218 280 281
Gallagher 12 93 185
Gauss 7 57 94 19 329
Gaussian component 51 94
Geometry, Plane Projective 12
Gershgorin 765 376
Gershgorin discs 165 316
Gnedenko 53 55 56 124
Gnedenko and Kolmogorov 24 26 25 29 49 50 57 53 54 55 56 57 17 125 167 201
Group of substitutions 13 183 209
Group of transformations 13 183 209
H lder 779 786 236 373 329 86 191 214 lder 779 786 236 373 329 86 191 214
Haar 63 68
Haar measure 63 68
hadamard 7 29
Hahn — Banach 787
Hal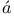 sz 70 72 27 77 774 224 225 226 233 252 255 256 286 308 372 377 330 337 83 86 125 209 211 212 222 260 285 286 289 296 297 301 303 311 312 sz 70 72 27 77 774 224 225 226 233 252 255 256 286 308 372 377 330 337 83 86 125 209 211 212 222 260 285 286 289 296 297 301 303 311 312
Halberstam 6 30 44 47 50 51 202
Halberstam and Davenport 72 185
Halberstam and Elliott 272
Halberstam and Richert 80 185
Halberstam and Roth 77
Hall 333
Hamel 76
Hamilton 339
Hamilton’s principle 339
Hardy 7 3 702 18 239 248 334
Hardy and Ramanujan 2 3 5 73 74 18 19 43 98 99 102 103 104 290 296 302 303 311
Hardy and Wright 85 89 108 112 778 733 734 224 138 139 170
Hardy — Little wood (Hardy and Littlewood) 2 77 102 254 348 357 358 255
Hardy — Littlewood (circle) method 2 6 9
Hardy — Littlewood tauberian theorem 77 254 348 351 358 255
Hardy — Littlewood tauberian theorem, (statement) 102
Hardy, Littlewood and P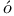 lya 186 lya 186
Hardy’s 1921
Hartman 292
Hausdorff 340
Hecke 227
Hecke’s dictum 227
Heilbronn 94 774
Heine — Borel 168
Hengartner and Theodorescu 278
hermite 72 762 766 258
Hermitian form, non-negative definite 258
Hermitian matrix, operator 162
Hermitian operator 12
Hermitian operator, spectral radius 12 162
Highest common divisor of a sequence 295
hilbert 787 785
Hilbert’s inequality 185
Hooley 41 332
Ibragimov and Linnik 78
Ikehara — Wiener 100 707 702
Improper distribution function 25
Independence and divisibility by primes 146 24
Independence in probabilistic number theory 4 146
Independent functions 24
Independent random variables 30
Infinite convolutions 37
Infinitely divisible law 49 145 147 167 168 199 201 204 209 338
Infinitely divisible law, characteristic function according to Kolmogorov 51
Infinitely divisible law, characteristic function according to L vy — Khinchine 49 50 vy — Khinchine 49 50
Infinitely divisible law, convergence of 53
Infinitesimal, variable 54 147
Ingham 248 249 258 260
Ingham’s review 248 258 260
Inner measure 159
Integral equation, approximate 11 213
Interval, positive bounded 72
Inversion formula 28
jacobi 75 321
Jacobi symbol 321
Jessen and Wintner 46 78 793
Jutila 329
K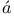 tai 34 37 50 51 120 331 333 tai 34 37 50 51 120 331 333
Kac 4 5 746 18 22 24 25 26
Kac — Erd s (Kac and Erd s (Kac and Erd s) 4 5 74 746 782 274 12 18 20 24 25 26 262 302 s) 4 5 74 746 782 274 12 18 20 24 25 26 262 302
Kac — Erd s theorem 18 262 s theorem 18 262
Kac — Kubilius — Erd s 9 31 48 125 s 9 31 48 125
Kac’ lecture, and Erd s 24 25 s 24 25
Kac’ letter 24
Kantorovich and Akilov 787
Karamata 78 77
Kesten 278
Khinchine 55 77 125 167
Khinchine and L vy 49 57 135 144 vy 49 57 135 144
Khinchine — L vy representation 49 50 57 144 vy representation 49 50 57 144
Kobayashi 72 785
Kolmogorov 3 32 44 45 57 52 53 56 77 277 13 17 24 27 37 205
Kolmogorov and Gnedenko 24 26 28 29 49 50 57 53 54 55 56 57 17 125 167 201
Kolmogorov’s inequality 44
Korevaar, van Aardenne — Ehrenfest and de Bruijn 78 77
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



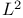 -norm
-norm  -module
-module  l
l  s
s 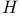 , additive functions
, additive functions 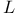 of Khinchine
of Khinchine 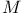 , laws
, laws 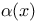
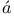 n — Kubilius inequality
n — Kubilius inequality 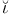 nle
nle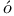 lya
lya