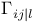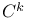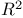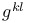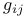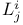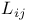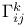|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Millman R.S., Parker G.D. — Elements of Differential Geometry |
|
|
 |
| Предметный указатель |
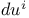 as a linear functional 100 as a linear functional 100
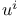 -curve 84 -curve 84
 -neighborhood 88 -neighborhood 88
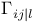 105 105
Angle between vectors 3 181
Angular excess 187
Angular variation 182
Angular velocity vector 35 (4.11)
Antipodal points 162
Arc length 20
Arc length, of a surface curve 95
Arc length, reparametrization by 21
Area 130 135
Area element 130
Asymptotic curve 134
Asymptotic curve, of a developable surface 140 (8.53)
Asymptotic direction 134 138
Atlas 204
Axis of a helix 32
Axis of revolution 86 (1.2)
Ball of radius  200 200
Barbier's Theorem 70
Basis 2
Basis, orthonormal 3
Beltrami — Enneper Theorem 139 (8.35)
Bertrand curves 38 41 48
Bertrand curves, characterization 38 (4.31)
Bertrand mate 38
Bertrand mateof a circular helix 46 (5.6)
Binormal 26
Binormal spherical image 36
Bisect a curve 163
Bonnet's rigidity theorem 151
Bound 181
Boundary 181
Bounded set 174
Bump function 215 (3.6)
Catastrophe theory 246
Catenoid 137 (8.15) 146 147 148
Cauchy — Schwarz inequality 3
Chern — Hopf Conjecture 241
Christoffel symbol 104 105
Christoffel symbol of a connection 224
Christoffel symbol, intrinsic formula 105
Circle of latitude 86 (1.2)
Class 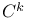 11 209 11 209
Closed set 174
Codazzi — Mainardi equations 142
Coefficients of the Riemannian metric 93
Compact 174
complete 112 238
Components of a vector 2
Cone 207
Cone $$g_{ij} 101 (3.7)
Cone as a developable surface 141 (8.56)
Conjugate directions 134 138
Conjugate family of curves 139 (8.31)
Connection 224
Connection, for a submanifold 241 (8.7)
Connection, metrical 234
Connection, Riemannian 232 236
Connection, symmetric 235
Connection, torsion-free 235
Contact: of a surface 138 (8.29)
Contact: spherical 39
Continuous function: from a surface to 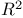 89 89
Continuous function: in a metric space 201
Contravariant transformation 98
Convex curve 60
Convex surface 193
Coordinate chart 203
Coordinate function 212
Coordinate patch 77
Coordinate transformation 79
Coordinate transformation, effect on 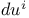 101 101
Coordinate transformation, effect on 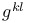 97 97
Coordinate transformation, effect on 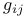 96 96
Coordinate transformation, effect on 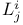 127 (7.6) 127 (7.6)
Coordinate transformation, effect on 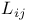 108 (4.4) 108 (4.4)
Coordinate transformation, effect on 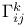 108 (4.11) 108 (4.11)
Coordinate transformation, effect on g 97
Coordinate transformation, effect on tangent vectors 85
Covariant derivative 116 (5.14) 224 225
Covariant transformation 98
Cover 89 204
Crofton's Formula 168
Cross product 6
Curvatura integra 189
Curvature: center of 39 (4.34) 41
Curvature: Gaussian 127 130 174 242
Curvature: Gaussian, formula 137 (8.6 8.7)
Curvature: Gaussian, intrinsic formula 143
Curvature: geodesic 103
Curvature: geodesic, extrinsic formula 106
Curvature: geodesic, intrinsic formula 106
Curvature: mean 127 130 242
Curvature: mean, formula 137 (8.3 8.11)
Curvature: normal 103
Curvature: of a plane curve 25 52
Curvature: of a regular curve 24
Curvature: of a regular curve, motivation 24
Curvature: principal 129
Curvature: radius of 34 39
Curvature: radius of, of an oval 72 (5.6 5.9)
Curvature: Ricci 239
Curvature: scalar 240
Curvature: sectional 239
Curvature: total 161 189
Curve: asymptotic 134
Curve: binormal to 26
Curve: closed 53
Curve: convex 60 63
Curve: curvature 24 (see also Curvature)
Curve: evolute 40
Curve: Fundamental Theorem 42
Curve: geometric 14
Curve: involute 40
Curve: knotted 169
Curve: length 20
Curve: length minimizing 112
Curve: maximally straight 120
Curve: parametric 84
Curve: piecewise regular 58
Curve: plane 29 (3.6 3.7) 41 45 5.3)
Curve: plane, Bertrandmate 38 (4.32)
Curve: plane, characterization 31 34 36 4.16) 37 4.20) 48
Curve: plane, curvature 25 52
Curve: plane, evolute 41 (4.43)
Curve: plane, involute 41 (4.40 4.41)
Curve: plane, normal vector field 52
Curve: plane, rotation index 55 58
Curve: plane, spherical contact 40 (4.36)
Curve: plane, tangent circular image 58
Curve: plane, tangent vector field 52
Curve: polar axis 39 (4.34)
Curve: principal normal 26
Curve: radius of curvature 34 39
Curve: radius of torsion 34
Curve: regular 15
Curve: reparametrization 17
Curve: reparametrization, by arc length 21
Curve: segment 20
Curve: segment, reparametrization 23 (2.7)
Curve: simple 54
Curve: speed 15
Curve: sphere 19 (1.7) 34 37 45
Curve: sphere, characterization 33 37 4.25 4.26) 38
Curve: sphere, normal curvature 107 108
Curve: sphere, torsion 171
Curve: spherical contact 39
| Curve: tangent developable surface 88 (1.14)
Curve: tangent line 16
Curve: tangent vector field 15
Curve: unit speed 22 24
Curve: unknotted 169
Curve: velocity vector 15
Curve: vertex of 41 (4.44) 66
Curvilinear coordinate system 84
Cusp 71 (5.5)
Cylinder 115 (5.10) 140 152
Cylinder, 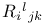 144 (9.4) 144 (9.4)
Cylinder, as a developable surface 141 (8.56)
Cylinder, curvature of 136 (8.1)
Cylinder, L 127 (7.2)
Darboux vector 35 (4.11)
Developable surface 140
Developable surface, characterization 140 (8.49)
Developable surface, Gaussian curvature 140 (8.52)
Diffeomorphism 223 (5.4)
Differentiable function: of a manifold to R 209
Differentiable function: of a surface to R 124 145
Differentiable function: of manifolds 209
Differentiable function: of surfaces 146
Differentiable vector field 117
Differential of a mapping 219
Dimension: of a manifold 204
Dimension: of a vector space 2
Directional derivative 124
Distance 237
Drag curve 158
Dual basis 100
Dual space 100
Dupin indicatrix 131 138
Dupin indicatrix, asymptotes 134
Eigenvalue 5 128
Eigenvector 5 128
Ellipsoid 88 (1.12) 91 92
Elliptic integral 23
Elliptic paraboloid 88 (1.11) 108
Elliptic point 132 138
Embedding 221
Euclid's Fifth Postulate 188 (4.5) 231
Euler characteristic 188 190
Euler's theorem 129
Evolute of a curve 40
Existence and uniqueness theorem: for curves 42
Existence and uniqueness theorem: for geodesies 111 231
Existence and uniqueness theorem: for parallel vector fields 118 228
Existence and uniqueness theorem: for Riemannian connections 236
Existence and uniqueness theorem: for surfaces 151
Fary — Milnor Theorem 73 169
Fenchel's Theorem 72 165 170
Field of metrics 233
Field of vectors 216
First fundamental form 94
Flat Euclidean space: connection of 224 227
Flat Euclidean space: covariant derivatives 226
Flat Euclidean space: curvature 242 (8.11)
Flat Euclidean space: geodesies 232 (7.1)
Flat Euclidean space: parallel vector fields 228
Flat Euclidean space: Riemannian connection 241 (8.4)
Flat point (Planar point) 132
Four-vertex theorem 66
Frenet — Serret apparatus 26
Frenet — Serret equations 30
Frenet — Serret Theorem 30
Fundamental lemma of Riemannian geometry 231
Fundamental Theorem of Curves 42
Fundamental Theorem of Surfaces 151
Gauss — Bonnet formula 173 185
Gauss — Bonnet theorem 188
Gauss — Bonnet Theorem, generalization 191
Gauss's equations 141
Gauss's formulas 104 241
Gauss's Theorema Egregium 143 149
Gaussmap 131 180
Genus 190
Geodesic 109
Geodesic coordinate patch 115 (5.5) 176
Geodesic, as an asymptotic curve 138 (8.28)
Geodesic, characterization 109 110
Geodesic, differential equation 109 115 5.8)
Geodesic, existence and uniqueness theorem 111
Geodesic, image under isometries 152 (10.5)
Geodesic, on a manifold 230
Geodetic torsion 137 (8.13)
GL(n, R) 205
Graph of a function 78
Green's theorem 51
Hadamard's Theorem 193
Helicoid 87 (1.4) 138 146 147 148 153
Helicoid, as a ruled surface 139 (8.36)
Helicoid, lineofstriction 140 (8.41)
Helix 46 (5.5) 48 115
Helix, axis 32 35
Helix, characterization 35 (4.3) 37
Helix, circular 17 23 2.3) 26 32
Helix, circular, Bertrand mate 46 (5.6)
Helix, circular, characterization 46 (5.4 5.6)
Helix, general 32
Helix, general form 44—45
Helix, involute 41 (4.40)
Helix, Lancret's characterization 32
Helix, pitch 32 35
hemisphere 162
Hilbert's theorem 238
Homogeneous coordinates 200
Hopf — Rinow theorem 238
Hyperbolic cosine 12
Hyperbolic disk see Poincare disk
Hyperbolic half plane 179 (2.4) 188 4.3 4.5)
Hyperbolic half plane, connection 225
Hyperbolic half plane, covariant derivatives 227 (6.3)
Hyperbolic half plane, distance 241 (8.8)
Hyperbolic half plane, geodesies 231
Hyperbolic half plane, parallel translation 229
Hyperbolic half plane, parallel vector fields 228
Hyperbolic half plane, Riemannian connection 241 (8.5)
Hyperbolic half plane, Riemannian metric 234
Hyperbolic paraboloid 87 (1.5) 91 111
Hyperbolic paraboloid, as a ruled surface 139 (8.37)
Hyperbolic paraboloid, asymptotic curves 138 (8.27)
Hyperbolic paraboloid, geodesies 115 (5.9) 116
Hyperbolic point 132 138 8.23)
Hyperbolic secant 231
Hyperbolic sine 12
Hyperbolic space form 242 (8.13)
Hyperbolic tangent 231
Hyperboloid of one sheet 91
Hyperboloid of one sheet, as a ruled surface 139 (8.38)
Hyperboloid of one sheet, geodesies 115 (5.11) 116
Hyperboloid of two sheets 92
Hypersurface defined by f 203 206 221 241
Hypersurface defined by f, tangent space 222
Immersion 223
Implicit function theorem 202
Index of a vector field 195
Inner product 2
Intrinsic normal 103
Inverse function theorem 202
Involute of a curve 40
Isometric 147
Isometric, locally 147
Isometry 147 234
Isometry, local 147
Isometry, orientation preserving 152 (10.8)
Isomorphism 4
Isoperimetric inequality 64
Jacobi's identity 218
Jacobi's theorem 162
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



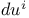 as a linear functional
as a linear functional 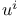 -curve
-curve  -neighborhood
-neighborhood