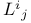|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Millman R.S., Parker G.D. — Elements of Differential Geometry |
|
|
 |
| Предметный указатель |
Jacobian 79 201 220
Jordan curve theorem 59
Kronecker symbol 3
Lancret's Theorem 32
Left invariant vector field 223 (5.5)
Length minimizing curves 112
Length of a curve 20 237
Length of a vector 2
Level surface 91
Level surface, orientability 181
Lie bracket 144 (9.5) 217
Lie group 209 223
Line integral 50
Line of curvature 129
Line of curvature, as an asymptotic curve 139 (8.33)
Line of curvature, of a developable surface 140 (8.53)
Line of curvature, of a surface of revolution 137 (8.5)
Line of striction 140 (8.40)
Line: as a geodesic 115 (5.4)
Line: as an asymptotic curve 138 (8.26)
Line: characterization 28 33 36 4.16) 48
Line: equation 8
Linear functional 100
Linear transformation 4
Linear transformation, eigenvalues and eigenvectors 5
Linearly dependent and independent vectors 2
Logarithmic spiral 19 (1.6) 45
M(n) 205 208
Manifold 204
Manifold, dimension 204
Manifold, product 208 (2.2)
Manifold, tangent space 213
Maximally straight curve 120
Measure of a set 167
Meridian 86 (1.2)
Metric coefficients 93
Metric space 200
Metric: induced 234 241
Metric: nondegenerate 240
Metric: Riemannian 233
Metric: topological 200
Meusnier's Theorem on umbilics 175
Minimal surface 130 137
Minimal surface, characterization 138 (8.17)
Mixed scalar product 7
Moebius band 87 (1.9)
Moebius band, as a ruled surface 139 (8.36)
Moebius band, as a surface 92 (2.5)
Moebius band, line ofs triction 140 (8.41)
Moebius band, nonorientability 87 (1.9) 181
Monge patch 78
Monge patch, 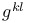 101 (3.3) 101 (3.3)
Monge patch, 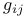 94 94
Monge patch, 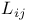 106—107 106—107
Monge patch,  106—107 106—107
Monge patch, area formula 136
Monotone 60
Moving frame 28
Moving trihedron 28
n-sphere 203 205 208 215
n-sphere, curvature 242 (8.11)
n-torus 208 (2.3)
Neighborhood 200
Non-unit speed curves 46—48
Nonhomogeneous coordinates 205
Normal plane 31 37
Normal space 103
Normal space, of a submanifold 241 (8.7)
Normal spherical image: of a curve 36 162
Normal spherical image: of a surface 131
Normal vector field: of a plane curve 52
Normal vector field: of a regular curve 26
Normal vector field: of a surface 81
Null-homotopic 182
O(N) 208 (2.5)
Open set: in a metric space 200
Open set: in a surface 123
Open set: in the plane 76
Opposite point: on an oval 69
Opposite point: on an ovaloid 194 (6.1)
Orientable surface 180
Orientation of a vector space 6
Orientation of a vector space, right handed 6
Oriented great circle 167
Orthogonal net 101 (3.4)
Orthogonal vectors 3
Orthonormal basis 3
Osculating circle 39 (4.34)
Osculating paraboloid 138 (8.29)
Osculating plane 31
Osculating plane, equation 35 (4.7)
Osculating sphere 39 (4.35)
Oval 66 71 72 5.7 5.8 5.9)
Oval, constant width 69
Oval, constant width, Barbier's Theorem 70
Oval, width 69
Ovaloid (Convex surface) 193
Parabolic point 132 138
Parallel translation 118
Parallel translation, and metrical connections 234
Parallel translation, on a manifold 229
Parallel vector field: along a curve 117 228
Parallel vector field: differential equation 117
Parallel vector field: existence and uniqueness 118
Parallel vector field: on a manifold 229
Parallelism defined by a curve 122 (6.5)
Parallelizable manifold 218 (4.6) 232
Parametric curves 84
Parametric curves, as a conjugate family of curves 139 (8.32)
Parametric curves, as asymptotic curves 138 (8.24)
Period of a closed curve 53
Perpendicular see Orthogonal net Orthogonal
Picard's theorem 42
Planar point (Flat point) 132
Plane: 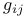 101 (3.6) 101 (3.6)
Plane: 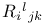 144 (9.1) 144 (9.1)
Plane: curvature of 136 (8.1)
Plane: equation of 9
Plane: geodesic curvature in 108 (4.6)
Plane: normal 31
Plane: osculating 31
Plane: parallel vector fields in 117
Plane: rectifying 31
Plethora 246
Poincare disk 179 (2.5) 188 4.4 4.5) 242
Poincare — Brouwer Theorem 196
Polar axis 39 (4.34)
Polygon 187 (4.1) 188 191
Principal curvatures 129
Principal directions 129
Principal normal vector field 26
Product manifold 208 (2.2)
Projective n-space 200 203 1.2) 205 215
Projective plane 200 223 5.6)
Proper coordinate chart 203
Proper coordinate patch 89
Pseudo-sphere 158
Raising an index 126
Rectifying plane 31
Reflection through a point 103
Region 181
Regularity condition for surfaces 77
Reparametrization: by arc length 21
Reparametrization: of a curve 17
Reparametrization: of a curve segment 23 (2.7)
Reparametrization: of a surface 79
Riemann — Christoffel curvature tensor: Riemannian connection 232 236
Riemann — Christoffel curvature tensor: type (0, 4) 239
Riemann — Christoffel curvature tensor: type (l 3) 238
Riemannian curvature tensor 141 143
| Riemannian curvature tensor, coefficients 141 242
Riemannian curvature tensor, invariant definition 145 (9.10)
Riemannian curvature tensor, symmetry properties 144 (9.2) 145
Riemannian manifold 233
Riemannian metric 233
Right handed orientation 6
Rigid motion 150
Rigidly equivalent 150
Rotation 150
Rotation index 55 58
Rotation Index Theorem 56 161
Ruled surface 139
Ruled surface, curvature 139 (8.39)
Ruled surface, line of striction 140 (8.40)
Ruled surface, noncylindrical 140
Ruled surface, singular point 139
Second fundamental form 123
Second fundamental form, coefficients 104
Second fundamental tensor of a submanifold 241 (8.7)
Self-adjoint linear transformation 127
Simply connected 185
SL(n) 201
span 2
Special orthogonal matrix 150
Speed of a curve 15
Sphere 87 (1.10) 88 108 4.10) 185 187 209 215 223
Sphere of dimension n see n-sphere
Sphere, 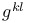 96 96
Sphere, 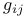 94 98 101 94 98 101
Sphere, 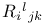 144 (9.3) 144 (9.3)
Sphere, angular excess 187
Sphere, angular variation 184
Sphere, area formula 136
Sphere, as a surface 90 92
Sphere, curvature of 136 (8.1)
Sphere, Dupin indicatrix 132 138
Sphere, equation 10
Sphere, Euler characteristic 190
Sphere, g 96
Sphere, geodesies 110 115 232
Sphere, L 127 (7.1)
Sphere, normal to 102 108
Sphere, orientability 180
Sphere, parallel translation on 118—119 121
Sphere, parallel vector fields 117
Sphere, simply connected 185
Sphere, stereographic projection 87 (1.10)
Spherical image 36
Stereographic projection 87 (1.10)
String involute 71 (5.5)
Submanifold 221
surface 89
Surface of revolution 86 (1.2) 179
Surface of revolution, 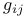 101 (3.1) 101 (3.1)
Surface of revolution, 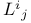 127 (7.5) 127 (7.5)
Surface of revolution, 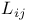 108 (4.2 4.3) 108 (4.2 4.3)
Surface of revolution, as a surface 92 (2.1)
Surface of revolution, axis 86 (1.2)
Surface of revolution, circle of latitude 86 (1.2)
Surface of revolution, curvature 127 (7.5) 137 159
Surface of revolution, developable 140 (8.48)
Surface of revolution, geodesies 110 115 5.6)
Surface of revolution, lines of curvature 137 (8.5)
Surface of revolution, meridian 86 (1.2)
Surface of revolution, minimal 138 (8.18)
Surface of revolution, of constant curvature 153
Surface of revolution, principal curvatures 137 (8.10)
Surface, arc length on 95
Surface, complete 112
Surface, convex 193
Surface, first fundamental form 94
Surface, Fundamental Theorem 151
Surface, metric coefficients 93
Surface, minimal 130
Surface, normal space 103
Surface, normal to 81
Surface, of constant curvature 178
Surface, of constant width 194 (6.1)
Surface, orientable 180
Surface, simple 77
Surface, tangent plane 81
Surface, tangent space 93
Tangent circular image 58
Tangent developable surface 88 (1.14) 140
Tangent developable surface, 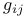 140 (8.47) 140 (8.47)
Tangent developable surface, as a developable surface 141 (8.56)
Tangent developable surface, as a ruled surface 139 (8.36)
Tangent developable surface, line of striction 140 (8.41)
Tangent line to a curve 16
Tangent plane 81
Tangent space: basis 84
Tangent space: to a manifold 213
Tangent space: to a surface 93
Tangent spherical image 36
Tangent spherical image, curvature and torsion 48 (6.10)
Tangent vector field 15
Tangent vector field, invariance under reparametrization 18
Tangent vector field, of a plane curve 52
Tangent vectors: as a vector space 84 213
Tangent vectors: on a manifold 210
Tangent vectors: on a surface 83
Taylor's theorem 213
Tensor of type (1, 1) 126
Theorema egregium 143 149
Torsion: geodetic 137 (8.13)
Torsion: of a curve 26 139
Torsion: of a sphere curve 171
Torsion: radius 34
Torus 86 (1.1) 152 181 197
Torus, 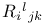 144 (9.4) 144 (9.4)
Torus, as a surface 92 (2.2)
Torus, curvature of 136 (8.1)
Torus, L 127 (7.3)
Torus, not simply connected 185
Torus, orientability 180
Total angular variation 182
Total curvature of a curve 161
Total curvature of a surface 189
Total index of a vector field 196
Total torsion 170
Tractrix 158
Triple scalar product 7
Umbilic 129
Umbilic, Meusnier's Theorem 175
Unit circle 58 169
Unit disk 169
Unit normal to a surface 81
Unit speed curve 22 24 237
Vector field: along a curve 116 225
Vector field: existence 218 (4.2)
Vector field: on a manifold 216
Vector product 6
Vector space 1
Vector space, basis 2
Vector space, dimension 2
Vector space, orientation 6
Vectors: angle between 3
Vectors: components 2
Vectors: linearly dependent and independent 2
Vectors: orthogonal 3
Velocity vector 15
Vertex 41 (4.44) 66
Vertex, Four-Vertex Theorem 66
Weingarten map 125
Weingarten map, coefficients 125
Weingarten's equations 126
Whitehead's Theorem 238
Whitney embedding theorem 222
Width: of an oval 69
Width: of an ovaloid 194 (6.1)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте