|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Schneider R. — Convex Bodies: The Brunn-Minkowski Theory |
|
|
 |
| Предметный указатель |
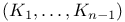 -extreme vector 76 -extreme vector 76
 metric 59 metric 59
Abstract, convex cone 42
Abstract, Steiner point 178
Adapted, one convex body to another 374
Additive function 173
Affine combination x
Affine hull x
Affine isoperimetric inequality 419
Affine quermassintegral 387
Affine surface area 419
Affinely independent points x
Ahrens, I. 3.1
Aleksandrov — Fenchel inequality 327
Aleksandrov — Fenchel — Jessen theorem 400 407
Aleksandrov, A.D. 1.5 1.7 2.2 2.4 2.5 3.5 4.2 4.3 4.6 5.1—5.3 6.2—6.6 6.8 7.1 7.2 Appendix
Alexander, R. 3.5
Alfsen, E.M. 1.4
Allendoerfer, C.B. 4.2
Ambartzumian, R.V. 3.5
Anderson, R.D. 2.2
Anikonov, Ju. E. Appendix
Approximable convex body 162
Area measure 203
Area measure of order m 207
Area measure, mixed 274
Arnold, R. 5.4
Arrow, K.J. 3.1
Artstein, Z. 3.1
Ash, R.B. 4.1
Asplund, E. 1.5 2.1
Associated bodies 140
Assouad, P. 3.5
Asymmetry class 156
Baddeley, A.J. 4.4
Baebler, F. 6.2
Bair, J. 1.3 1.4 3.1 3.2
Baire space 119
Ball, K. 7.4
Banchoff, T.F. 4.4
Bandle, C. 6.2
Bandt, Ch. 1.8
Bangert, V. 1.5
Baniegnic, R. 1.8
Baraki, G. 1.8
Barthel, W 6.1 6.2
Barycentre function 21
Batson, R.G. 14
Bauer, H. 1.4 4.1
Baum, D. 1.7
Beer, G.A. 1.8
Bensimon, D 2.1
Benson, D.C. 6.2
Berg, Ch. 3.3 3.4 4.3 Appendix
Bernstein, D.N. 6.3
Berwald, L. 4.5
Besicovitch, A.S. 2.2 2.3
Betke, U. 3.5 4.2 4.5 5.3 6.2 7.4
Bettinger, W. 6.2
Bieberbach inequality 318
Bieberbach, L. 6.2
Biiranv, I. 2.3 2.6 7.1
Bing, R.H. 2.3
Bjorck, G. 2.1
Blackwell, D 3.5
Blaschke diagram 322
Blaschke diagram, Hausdorff metric 58
Blaschke diagram, Santalo inequality 387 421 425
Blaschke selection theorem 50
Blaschke sum 394
Blaschke symmetrization 165
Blaschke's rolling theorem 150
Blaschke, W. 1.8 2.5 3.2 3.3 3.5 4.3 4.5 5.3 5.4 6.1 6.2 6.4 7.1 7.4 Appendix
Blind, R. 7.2
Blumenthal, L.M. 1.8
Bocek, L. 6.2
Body of constant width 128
Bohm, J. 3.4
Bokowski, J. 2.4 4.5 5.3 6.2
Bol, G. 3.1 6.2 6.5—6.7 Appendix
Bolker, E.D. 3.5
Boltjanski, W.G. 3.5 6.5
Bonnesen, T. 1.7 2.2 3.1 3.3 4.3 5.1 5.3 5.4 6.1 6.2 6.4 6.7 7.1 7.3
Bonnesen-style inequalities 323
Bonnice, W. 1.3
Boolean model 256
Boroczky, K. 7.1
Borwein, J.M. 3.1
Bose, R.C. 5.4
Botts, T. 1.2
Bourbaki, N. 1.3 1.4 2.1 2.2
Bourgain, J. 3.3 3.5 6.1 6.2 7.2 7.4 Appendix
Brascamp, H.J. 6.1
Brehm, U. 4.4
Brondsted, A. 1.4 2.2 2.4 3.4
Bronshtein, E.M. 1.8 2.1 3.2 7.1
Brooks, J.N. 3.2
Brown, A.L. 2.1
Brunn — Minkowski inequality 309
Brunn — Minkowski inequality, extended 383
Brunn — Minkowski theorem 309
Brunn — Minkowski theorem, general 339
Brunn, H. 6.1
Budach, L. 4.4
Buldygin, V. V 6.1
Bunt, L.N.H. 1.2
Burago, Ju, D 1.2 1.3 6.1—6.3
Burckhardt, J.J. 3.5
Burton, G.R. 2.1 3.2 3.5 4.5
Busemann intersection inequality 417
Busemann — Petty centroid inequality 418
Busemann's theorem 316
Busemann, H. 1.5 2.5 4.6 6.1—6.3 6.8 7.1 7.2 7.4
Campi, S. 7.2 7.4 Appendix
Canal class 377
CAP 81
Cap-body 76
Cap-covering theorem 81 84
Caratheodory's theorem 3
Caratheodory, C 11
Cassels, J.W. S. 3.1
Cauchy's surface area formula 295
cc-hyperspace 57
Centred convex body 383
Centroid body 417
Chakerian, G.D. 3.1 3.5 6.2 6.5 7.1—7.4
Chebyshev set 11 67
Chebyshev subspace 94
Cheeger, J. 4.4
Chemoff, P.R. Appendix
Cheng, S.-Y. 7.1
Chern, S.S. 2.5 4.5 5.3 7.2
Choquet theory 20
Choquet, G. 1.4 2.1 3.5
Christoffel's problem 216 218
Christoffel, E. B 4.3
Cieslak, W. Appendix
Circumball 129
Circumradius 129
Clack, R. 7.4
Class asymmetry 156
Class canal 377
Class, universal approximating 162
Closed convex function 35
Closed convex hull 6
Closed halfspace xi
Closed segment x
Closing of set A by set B 138
Coifman, R.R. Appendix
Collier, J.B. 2.1
| Combination 1
Combination, affine x
Combination, convex 1
Combination, linear x
Combination, positive 2
Concave function 21
Conditionally positive definite function 194
Cone 80
Cone, convex 1
Cone, convex, abstract 42
Cone, convex, normal 70
Cone, convex, projection 70
Cone, convex, recession 17
Cone, convex, touching 74
Conjugate function 36
Contact measure 260
Convex body 8
Convex body, adapted 347
Convex body, approximable by a class 162
Convex body, centred 383
Convex body, decomposable 150
Convex body, determined by closed set 321 343
Convex body, equivalent by dilatation 383
Convex body, freely rolling 150
Convex body, freely sliding 143
Convex body, indecomposable 150 157 172
Convex body, irreducible 141 156
Convex body, k-curved 121
Convex body, normalized 150
Convex body, reducible 141 156
Convex body, stable 67
Convex body, strictly convex 77
Convex body, typical 119
Convex cone 1
Convex function 21
Convex hull 2
Convex ring 175
Convex set 1
Convex set, continuous 46
Convexity number 225
Corson, H.H. 2.1
Coxeter, H.S. M. 3.5
Cressie, N. 3.1
Critical set 141
Crofton's intersection formula 235
Curtis, D.W. 1.8
Curvature 104
Curvature centroid 305
Curvature function 419
Curvature image 420
Curvature measure 203
Curvature measure, generalized 202
Curvature, Gauss — Kronecker 106
Curvature, integral of mean 216
Curvature, Jessen radius of 117
Curvature, lower 104
Curvature, lower radius of 104
Curvature, mean 106
Curvature, principal 105
Curvature, principal radii of 108
Curvature, specific 269
Curvature, upper 104
Curvature, upper radius of 104
Curved convex body 121
Czipszer, J. 6.5
Dalla, L. 2.1
Danzer, L. 1.1 1.3
Das Gupta, S 6.1
Davis, C. 1.3
Davy, P.J. 4.5 5.4
Debrunner, H. 5.3
Debs, G. 2.1
Decomposable convex body 150
Defined locally, measure 206
Deicke, A. 7.4
Delgado, J.A. 3.2
Determined by closed set, convex body 321 343
Diameter xi
Dierolf, P. 1.8
Difference body 127 409
Difference body inequality 409
Dilatation xii 138
DIMENSION 7
Dinghas, A. 1.8 3.1 5.3 6.1 6.2 6.5 6.7 Appendix
Direct sum xi
Direct summand 142
Directly indecomposable 142
Diskant, V.I. 6.1 6.2 6.4 6.5 6.7 7.2
Distance xi
Dor, L.E. 3.5
Dresevic, M. 1.8
Dual affine quermassintegral 387
Dual cone 34
Dual mixed volume 385
Dual quermassintegral 386
Dubins, L.E. 1.4
Dubois, C 3.1
Dudley, R. 1.5 1.8
Dupin indicatrix 116
Dupin, Ch, 7.4
Duporcq, E. 5.4
Dziechcinska-Halamoda, Z. 3.1
Eckhoff, J. 1.1 3.4 4.5
Edelstein, M 2.1 3.1
EDGE 96
Effective domain 22
Efimov, N.W. 6.6
Eggleston, H.G. 2.1 6.2 7.3
Egorychev, G.P. 6.8
Eifler, L.Q. 2.1
Ekeland, I. 3.1
Endomorphism 170
Envelope 67
Epelman, M.S. 2.2
Epigraph 22
Equivalent by dilatation, convex bodies 383
Equivalent by telescoping, convex bodies 380
Equivariant map 166
Equivariant under rigid motions, Steiner point 43
Erosion 138
Euler characteristic 175
Euler point 116
Euler relation 179
Euler's theorem 106
Euler-type relation 180
Even measure 183
Ewald, G. 1.7 2.3 3.1 3.2 6.6
Exponent of entropy 60
Exposed 65
Exposed face 63 65
Exposed normal vector 74
Exposed point 19 65
Exposed r-skeleton 65
Exposed support plane 74
Extended Brunn — Minkowski inequality 383
Extended convex ring 256
Extended exterior normal vector 11 70
External angle 100
Extreme normal vector 74 76
Extreme point 18 65
Extreme ray 18
Extreme support plane 74 76
Face 18 62
Face, exposed 63 65
Face, isolated 79
Face, perfect 73
Face, proper 62
Face, strongly connected family of faces 152
Face-function 66
Facet 62 96
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



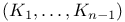 -extreme vector
-extreme vector  metric
metric