Авторизация
Поиск по указателям
Liu Q., Erne R. — Algebraic Geometry and Arithmetic Curves
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algebraic Geometry and Arithmetic CurvesАвторы: Liu Q., Erne R. Аннотация: This book is a general introduction to the theory of schemes, followed by applications to arithmetic surfaces and to the theory of reduction of algebraic curves. The first part introduces basic objects such as schemes, morphisms, base change, local properties (normality, regularity, Zariski's Main Theorem). This is followed by the more global aspect: coherent sheaves and a finiteness theorem for their cohomology groups. Then follows a chapter on sheaves of differentials, dualizing sheaves, and grothendieck's duality theory. The first part ends with the theorem of Riemann-Roch and its application to the study of smooth projective curves over a field. Singular curves are treated through a detailed study of the Picard group. The second part starts with blowing-ups and desingularization (embedded or not) of fibered surfaces over a Dedekind ring that leads on to intersection theory on arithmetic surfaces. Castelnuovo's criterion is proved and also the existence of the minimal regular model. This leads to the study of reduction of algebraic curves. The case of elliptic curves is studied in detail. The book concludes with the fundamental theorem of stable reduction of Deligne-Mumford. The book is essentially self-contained, including the necessary material on commutative algebra. The prerequisites are therefore few, and the book should suit a graduate student. It contains many examples and nearly 600 exercises.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2002Количество страниц: 463Добавлена в каталог: 21.05.2007Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Normalization, and flatness 136 Normalization, by blowing-up 341 Normalization, in an extension 120 278 Normalization, of a semi-stable curve 507—508 529 Nullstellensatz 30—31 Number field 58 Number field, ring of integers 58 69 112 139 268 454 Open subscheme 44 Open subscheme, of an affine Dedekind scheme 123 Ordinary double point 310 315 483 506 526 Ordinary double point, split 508 514 Ordinary multiple point 310 316 521 531 Ordinary multiple point, universal property 316 p-adic integers 18 Parameters (system of) 129 Path 471 Pic(X), Picard group 173 Picard group 192 261 408 538 Picard group, and group of Cartier divisors 257 261 264 Picard group, of a conic 418 Picard group, of a factorial domain 273 Picard group, of an affine line 346 Picard group, restriction to an open subset 401 Picard group, torsion points 299 540 Point, general 64 Point, generic 63 65 Point, of codimension 1 119 267 Point, regular 128 Point, singular 128 Point, with value in an algebraic extension 92 Poles see “Divisor of poles” Presheaf 33 Presheaf, injective morphism 35 Presheaf, morphism 35 Presheaf, surjective morphism 35 Principal closed subset 27 74 Principal open subset 27 51 Proj 321 Proj B, scheme associated to a graded algebra 52 Proj B, set of homogeneous prime ideals of a graded algebra 50 Projection formula 190 398 Projection, and base change 81 Projection, from a center 87 246 Projection, to a component 78 Projective space 50 Projective variety 56 Property local, on the base 84 Pure (dimension) 68 Quasi-coherent sheaf 158 Quasi-compact (topological space) 33 Quasi-section 227 Quotient, of a ringed topological space by a group 41 Quotient, of a scheme by a group see scheme (quotient) Quotient, of an algebraic variety by an algebraic group 59 Radical ideal 63 Radical of an ideal 27 Ramification, index 265 289 Ramification, locus 290 347 Ramification, point 290 Rational functions see “Function field” Rational map 111 348 367 494 Rational map, domain of definition 111 Rational point 148 Rational points 53 388 468 498 Rational points, and Galois extension 93 Rational points, are closed 76 Rational points, of a projective scheme 54 Rational points, of a subscheme 49 Rational points, of an affine scheme 49 Rational section of a sheaf 266 Reduction 462 Reduction map 467—469 481 497 Reduction, additive 485 Reduction, bad reduction 462 466 Reduction, non-split multiplicative 485 Reduction, of rational points 468 Reduction, potential multiplicative 499 505 Reduction, potential semi-stable 499 Reduction, semi-Abelian 533 542—543 551 Reduction, split multiplicative 485 Reg(X), set of regular points of X 131 Regular element see “Regular sequence” Regular function 44 60 61 66 Regular function, extension of 118 Regular immersion 228 Regular ring 128—135 337 346 Regular scheme 128—135 140—144 Regular scheme, and branch locus 347 Regular scheme, and divisors 271 Regular scheme, and local complete intersection 232 Regular scheme, birational morphism to a 272 Regular scheme, blowing-up 325 Regular scheme, embedding in a smooth scheme 226 Regular scheme, is Cohen — Macaulay 337 Regular scheme, is universally catenary 338 Regular scheme, not smooth 142 Regular sequence 228 335 Regular sequence, and flat base change 338 Relative differential forms 210 (see also “Differential forms” “Dualizing Relative differential forms, module of 210—215 219 Relative differential forms, sheaf of 216—235 529 Relative differential forms, universal property 210 Residue field 11 37 46 Resolution of singularities see “Desingularization” Restriction map 33 Restriction, of a section 34 Restriction, of a sheaf 34 Riemann hypothesis 394 Riemann — Roch theorem 281—282 Riemann's theorem 279 Ring, Artinian 70 Ring, Cohen — Macaulay 337—345 Ring, factorial 130 Ring, graded 20 23 135 Ring, local 9 Ring, reduced 59 Ring, semi-local 146 344 Ringed topological space 37 Ringed topological space, morphism 37 S-scheme 47 S-valuation 354 Scheme 44 Scheme, base 47 Scheme, Cohen — Macaulay 338—346 Scheme, connected 66 97 110—111 200 208 266 331 Scheme, finite 76 Scheme, integral 65 Scheme, irreducible 62 (see also “Geometrically irreducible”) Scheme, local 66 Scheme, locally noetherian 55 Scheme, Noetherian 55 Scheme, non-separated 101 Scheme, of connected components 496—497 (see also “Group of components”) Scheme, of dimension 0 76 Scheme, projective 53 83 Scheme, proper 103 Scheme, pure see “Equidimensional” Scheme, quasi-compact 57—60 67 160 Scheme, quasi-projective 109 113 124 171 188 Scheme, quotient 59 113 124 146 526 531 Scheme, reduced 59 Scheme, separated 100 110 Scheme, singular 128 Scheme, smooth see “Smooth morphism” Scheme, unibranch 223 Scheme-theoretic closure 58 Section, germ of a 35 Section, intersection with the special fiber 388 Section, lifting 224 Section, of a fibered product 81 Section, of a presheaf 34 Section, of a scheme 49 Section, of a separated morphism 110 Section, with values in an extension 81 Segre embedding 108 177 Self-intersection 383 Semi-stable curve 510 Semi-stable curve, dualizing sheaf 509 Semi-stable curve, graph 511 Semi-stable curve, local structure 514 531 Semi-stable curve, quotient by a group 526 Semi-stable model 515 522 Semi-stable reduction 515 518 533 Semi-stable reduction, in characteristic 0 536 Separated topological space 27 Serre duality 236 Serre's criterion for affine schemes 187 193 Serre's criterion for normality 339 Sheaf 34 Sheaf, associated to a presheaf 36 39 Sheaf, conormal 229 Sheaf, constant 39 Sheaf, direct image 37 163 Sheaf, direct limit 192 Sheaf, flasque 190 264 Sheaf, flat 189 Sheaf, free 173 Sheaf, generated by global sections 158 169—171 177—178 285 359 440 Sheaf, higher direct image 189 Sheaf, image 36 Sheaf, inverse image 37 163 Sheaf, invertible 165 173 Sheaf, locally free 173 Sheaf, normal 229 Sheaf, of algebras 34 175 Sheaf, of graded algebras 321 Sheaf, of homogeneous algebras 321 Sheaf, of ideals 38 Sheaf, of meromorphic functions 255 263—266 Sheaf, of modules 157 Sheaf, of relative differential forms see “Relative differential forms” Sheaf, of rings 34 Sheaf, pull-back 163 Sheaf, quasi-coherent 158 Sheaf, quotient 36 Sheaf, skyscraper 40 Sheaf, stalk 35 Sheaf, structure 37 Sheaf, surjective morphism 35 Sheaf, torsion-free 174 Sheaf, twists 166 Sing(X), set of singular points of X 131 Smooth locus 224 227 494 Smooth morphism 142—149 Smooth morphism, and differentials 222 227 230 247 Smooth morphism, and lifting of rational points 224 Smooth morphism, and normality 339 Smooth morphism, and quasi-sections 227 Smooth morphism, and regularity 142 Smooth morphism, embedding 226 407 Smooth morphism, local structure 224 226 Smooth morphism, smooth fibers 352 (see also “Good reduction”) sp(X), underlying topological space of a scheme X 81 Spec A, spectrum of A 26 Spec 175 Spec 28 Special fiber see “Closed fiber” Specialization 63—64 467 Spectral sequence 196 522 Spectrum 26 Stable curve 506 510 Stable curve, automorphisms 520 529 Stable curve, dualizing sheaf 510—511 Stable model 515 Stable model, and canonical model 518 Stable reduction 515 523 533 Stable reduction, and base change 520 533 Stable reduction, and covering 544 Stable reduction, and purely inseparable base extension 552 Stable reduction, and semi-Abelian reduction 543 Stable reduction, Deligne-Mumford's theorem 533 Stable reduction, extension realizing the stable reduction 551—552 Stable reduction, of a Fermat curve 548 Stable reduction, potential 543 544 547 Stein factorization 208 Strict transform 324 331 402 411 Strictly normal crossings 378 Subgraph 471 483 Subscheme see “Closed subscheme” “Open Subsheaf 34 Subvariety 56 Supp 40 Supp D, support of a Cartier divisor 260 Supp M, support of a module 336 Supp Z, support of a cycle 267 Support 173 Support, of a Cartier divisor 260 274 Support, of a cycle 267 Support, of a sheaf 40 56 surface 75 317 Surface, any proper regular algebraic surface is projective 413 Surface, rational 427 Surface, ruled 427 System of parameters 129 t(X), toric rank of a curve 314 u(X), unipotent rank of curve 314 V(f), principal closed subset associated to f 27 74 V(I), closed subset defined by an ideal I 26 X(K), set of points of X with values in a field K 92 X(S), set of sections of an S-scheme X 49 Z(I), set of common zeros of the polynomials contained in I 31
Реклама
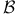, scheme associated to a homogeneous sheaf of algebras 
, spectrum of a quasi-coherent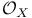 
-algebra 
, morphism of schemes associated to a ring homomorphism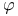 
, support of a sheaf 
|
|
О проекте