Авторизация
Поиск по указателям
Liu Q., Erne R. — Algebraic Geometry and Arithmetic Curves
Обсудите книгу на научном форуме Нашли опечатку?
Название: Algebraic Geometry and Arithmetic CurvesАвторы: Liu Q., Erne R. Аннотация: This book is a general introduction to the theory of schemes, followed by applications to arithmetic surfaces and to the theory of reduction of algebraic curves. The first part introduces basic objects such as schemes, morphisms, base change, local properties (normality, regularity, Zariski's Main Theorem). This is followed by the more global aspect: coherent sheaves and a finiteness theorem for their cohomology groups. Then follows a chapter on sheaves of differentials, dualizing sheaves, and grothendieck's duality theory. The first part ends with the theorem of Riemann-Roch and its application to the study of smooth projective curves over a field. Singular curves are treated through a detailed study of the Picard group. The second part starts with blowing-ups and desingularization (embedded or not) of fibered surfaces over a Dedekind ring that leads on to intersection theory on arithmetic surfaces. Castelnuovo's criterion is proved and also the existence of the minimal regular model. This leads to the study of reduction of algebraic curves. The case of elliptic curves is studied in detail. The book concludes with the fundamental theorem of stable reduction of Deligne-Mumford. The book is essentially self-contained, including the necessary material on commutative algebra. The prerequisites are therefore few, and the book should suit a graduate student. It contains many examples and nearly 600 exercises.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2002Количество страниц: 463Добавлена в каталог: 21.05.2007Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Dimension, of a ring 69 Dimension, of a topological space 68 Dimension, of a toric group 312 Dimension, of a unipotent group 306 Dimension, of fibers 137 154—156 Dimension, relative 240 Dimension, virtual relative 240 Discrete valuation ring 64 106 Discrete valuation ring, extension with prescribed residue field 517 Discrete valuation ring, linear equivalence 268 Discrete valuation ring, numerically effective 423 Discrete valuation ring, of poles 269 Discrete valuation ring, vertical 350 Discrete valuation ring, Weil 268 Discrete valuation ring, with normal crossings see “Normal crossings” Discrete valuation ring, with strictly normal crossings 378 Discriminant 446 div(f), principal Cartier divisor associated to a rational function 256 div(s), Cartier divisor associated to a rational section of an invertible sheaf 266 Div(X), group of Cartier divisors 256 Divisor, horizontal 349 Domination, a ring dominating a subring 106 Domination, a scheme dominating another one 330 Dual graph of a curve 473 511 Duality 243—247 281 Duality, for global complete intersections 250 Dualizing sheaf 243 389 Dualizing sheaf, and birational morphisms 403 Dualizing sheaf, degree 282 Dualizing sheaf, of a semi-stable curve 509 Dualizing sheaf, of a stable curve 510—511 Dualizing sheaf, of the projective space 242 Dualizing sheaf, on the canonical model 440 Dynkin diagrams 476 Eisenstein polynomial 116 Elimination of indeterminacy 112 396 Elliptic curve 217 (see also “Hyperelliptic curve”) Elliptic curve, differential forms 218 Elliptic curve, dualizing sheaf on the minimal regular model 423 447 Elliptic curve, filtration on the rational points 498 Elliptic curve, genus 280 Elliptic curve, group of components 497 Elliptic curve, has a hyperelliptic involution 288 Elliptic curve, integral equation 442 Elliptic curve, is an Abelian variety 491 Elliptic curve, minimal discriminant 447 Elliptic curve, minimal regular model 447 Elliptic curve, minimal Weierstrass model 447 449 Elliptic curve, Neron model 494 Elliptic curve, potential semi-stable reduction 501 Elliptic curve, reduction of the minimal regular model 485 Elliptic curve, Weierstrass equation 442 Elliptic curve, Weierstrass model 442 445 Elliptic equation 296 Embedded point 254 End vertex 471 Equidimensional 138 154 234 335 Etale, homomorphism 139 Etale, morphism 139—141 153 176 225 Etale, quasi-section 227 Etale, standard 153 Etale, topology 223 Euler — Poincare characteristic 205 278 Exact sequence 4 Excellent ring 342—344 Excellent scheme 342—347 361—362 Exceptional divisor 412 416—417 Exceptional locus 272 397 411 Extension of morphisms from a normal scheme to a proper scheme 119 Extension of scalars 3 Extension, purely inseparable 89—90 105 214 Extension, separable 89 215 226 342 Exterior algebra 236 f*D, inverse image of a Cartier divisor 262 Fermat curve 550 Fiber of a morphism 83 Fibered product 78 Fibered product, universal property 78 Fibered surface, minimal 418 Fibered surface, normal 347 Fibered surface, over a Dedekind scheme 347 Fibered surface, regular 347 Fibered surface, relatively minimal 418 Fibered surface, the set of regular points of a 343 Field, finitely generated 77 Filtration 16 20 498 Flat homomorphism 6 Flatness 6—15 137 144 144—146 176 207 235 346 347 Flatness, is a local property 10 Flatness, of a quotient algebra 14 139 Flatness, over a Dedekind domain 11 Flatness, over a Dedekind scheme 137 Formal completion 18—24 344 Formal completion, and action of a group 146 Formal completion, does not change the dimension 132 Formal completion, of a local ring of a semi-stable curve 512 Formal completion, of a regular local ring is regular 132 Formal completion, of a semi-local ring 146 Formal completion, of a topological group 17 Formal fiber 341 469—482 Formal functions (theorem on) 200 Formal group 482 Formal power series 18 Frac(A), total ring of fractions 255 Frobenius 94—99 301 394 Frobenius, absolute 94 Frobenius, and differentials 226 Frobenius, and flatness 145 Frobenius, and semi-stable curves 532 Frobenius, is purely inseparable 207 Frobenius, relative 94 Function field 66 77 277 Function, meromorphic 255 Function, rational 66 Fundamental divisor 436—438 450 g(X), genus of a smooth projective curve 279 Generic fiber 83 347 Genus 282 Genus, arithmetic 279 393 Genus, geometric 279 Geometric multiplicity 392 409 Geometrically connected 90—98 105 155 201 208 350—351 496 Geometrically integral 90—98 144 369 Geometrically irreducible 90—98 421 Geometrically reduced 90—98 105 131 209 369 Geometrically regular 342 Germ see “Section” Glueing, morphisms 40 Glueing, schemes 49 Glueing, sheaves 40 Going-down Theorem 545 Good reduction 462—464 479 502 545 Good reduction, potential 465 505 548 551 Grading 20 Graph 471 (see also “Dual graph”) Graph, branch in a graph 476 Graph, of a birational map 112 Graph, of a morphism 110 Graph, of a rational map 111 Grothendieck's vanishing theorem 188 Group of components 496 538 541 554 Group scheme 297—299 302 Group scheme, additive 298 Group scheme, commutative 298 Group scheme, multiplicative 298 Group scheme, toric 312 Group scheme, unipotent 306 316 Group, divisible 538 Group, uniquely 538 Height 69—72 76 332 337 Henselian discrete valuation ring 360 410 467—469 Henselian ring 360 Henselization 360 Higher direct image 189 204 208 Hilbert polynomial 284 Hodge index theorem 383 Homogeneous algebra 53 Homogeneous coordinates 53 Homogeneous element 20 Homogeneous ideal 50 Homomorphism, finite 29 Homomorphism, integral 29 33 69 Homomorphism, local 37 Horizontal divisor 349 ht(I), height of an ideal I 69 Hurwitz formula 289 Hyperelliptic curve 287 292 Hyperelliptic curve, bad reduction 466 480 Hyperelliptic curve, equation 296 Hyperelliptic curve, good reduction 464 480 Hyperelliptic curve, involution 294 I-adic topology 16 Idempotent 66 Identity component 496 504 Immersion 96 200 Immersion, closed 38 45 113 Immersion, open 38 45 Index of a curve 393 Inertia group 147 526 532 Integral closure 120 330 340 345 Integral equation 29 Intersection number 376 383 Inverse limit 16 Inverse limit, universal property 16 Inverse system 16 Irreducible component 62—63 97 Irreducible component, geometric 97 Isomorphism and base change 194 j(E), modular invariant of an elliptic curve 500 Jacobian conjecture 134 Jacobian criterion 130 134 147 Jacobian criterion, for projective varieties 134 Jacobian matrix 130 Jacobian variety 299 504 542 Jordan — Holder theorem 258 K(X), field of rational functions 66 k(x), residue field at a point x 37 Kahler differentials see “Relative differential forms” Klein curve 479 551 Krull's principal ideal theorem 71 Krull's theorem on the intersection of submodules 21 l(D), dimension of L(D) 279 L(D), global sections of 279 l.c.i. see “Local complete intersection” Leibniz rule 210 Length, of a module 258—259 262—265 274 Length, of a path 472 Leray acyclicity theorem 183 Lifting, infinitesimal 225 Lifting, of a closed point 468 Lifting, of rational points 224 Lifting, of the formal structure 235 Local complete intersection 232 338 339 438 451 510 Local ring 9 localization 9 Luroth's theorem 292 Meromorphic functions 255 Mittag — Leffler condition 24 Model 456 Model, minimal regular 418 422 455 Model, morphism 418 455 Model, of 482 (see also “Conic”) Model, of a surface 418 Model, of algebraic curves 455 Model, regular 455 Model, relatively minimal 418 Model, smooth 455 Model, with normal crossings 455 456 503 534 552 Modular curve 551 Modular invariant 500 Module, Artinian 259 Module, Cohen-Macaulay 337 346 Module, differential 178 Module, faithful 122 Module, faithfully flat 13 Module, flat 6 11 193 Module, graded 20 164 Module, of relative differential forms see “Relative differential forms” Module, simple 213 258 264 Module, torsion-free 8 Monoidal transformation 395 Mor(X, Y), set of morphisms from X to Y 47 Morphism, closed 103 Morphism, constant 137 Morphism, diagonal 100 216 Morphism, dominant 67 86 98 278 Morphism, faithfully flat 145 Morphism, finite 112—113 155 176 194 246 301 Morphism, finite and birational 362 Morphism, flat 136—139 145 Morphism, generically etale 227 Morphism, generically separable 227 249 Morphism, integral 112 120 545 Morphism, into a projective scheme 57 169 Morphism, into an affine scheme 48 57 Morphism, l.c.i. see “Local complete intersection” Morphism, of finite type 87 96 96—110 Morphism, of projective schemes 53 Morphism, of schemes 45 Morphism, open 58 145 Morphism, projection 78 Morphism, projective 83 108 Morphism, proper 103—107 110—112 194 Morphism, proper birational 150 371 373 408 Morphism, purely inseparable 200 207 207—208 291 419 532 Morphism, quasi-compact 58 67 96 163 188 Morphism, quasi-finite 97 140 152 155 Morphism, quasi-projective 109 112 152 155 Morphism, quotient 41 146 Morphism, ramified 290 294 Morphism, separable 289 Morphism, separated 100—102 Morphism, structural 47 Morphism, tamely ramified 290 300 Morphism, universally closed 103 Moving Lemma 379 380 391 429 Multiplicative subset 9 Multiplicity, intersection multiplicity 376 Multiplicity, of a Cartier divisor 260 Multiplicity, of a cycle 267 Multiplicity, of a hypersurface at a point 402 Multiplicity, of an irreducible component 305 352 368 392 Nagata ring 340—341 343 371—372 Nagata scheme 341 356 362 Nakayama's lemma 9 Neron model 489 494 504 Neron model, universal property 490 Neron — Ogg — Shafarevich's criterion 502 Nilpotent 28 32 Nilradical 31 60 Node in a graph 475 Noether's normalization lemma 29 155 Norm 77 272—274 Normal crossings 378 391 474 Normal crossings, strictly 378 Normal law 493 Normal ring 115—123 130 133 273 344 Normal scheme 115—126 130—131 152 201 269 339 545 Normalization 119—126 303 343 373 534 Normalization, and arithmetic genus 304
Реклама
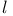-divisible 
|
|
О проекте