|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Levi-Civita T. — The Absolute Differential Calculus (Calculus of Tensors) |
|
|
 |
| Предметный указатель |
Relative motion 313 316
Relativity and Newtonian theory, differences 377
Relativity, composition of velocities in 317
Relativity, general, and Poisson’s equation 386 387
Relativity, general, postulates of 364
Relativity, invariance in 322
Relativity, kinematics of 311 316
Relativity, metrics, qualities of 325
Relativity, metrics, statical 326
Relativity, metrics, stationary 326
Relativity, postulates of 364
Relativity, principle of 311
Relativity, restricted 300
Relativity, Special Theory of 300
Reversibility of light propagation 365
Reversible motion 327
Reversible motion, transformation 3 7 61
Ricci 14 148 182 183 199 200 235 257 263 268 271 278 372 380 385 389 411
Ricci’s coefficients of rotation 268
Ricci’s lemma 148 152
Ricci’s symbols 199 372 389 411 426
Ricci’s tensor 199
Ricci’s tensor, linear invariant of 200 380
Riemann 172 175 176 177 178 179 180 181 182 184 193 195 196 200 209 215 216 219 220 221 224 225 228 232 233 234 236 240 242 243 244 247 257 261 278 374 376 378 379 384 389 414 417 426 430 436 437
Riemann — Christoffel tensor in 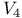 372 372
Riemann — Christoffel tensor in 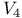 , 20 components of 372 (see also “Riemann’s symbols”) , 20 components of 372 (see also “Riemann’s symbols”)
Riemannian curvature of  195—198 195—198
Riemann’s symbols 172
Riemann’s symbols and conformal representation 228 246
Riemann’s symbols and Euclidean metric manifold 242—246
Riemann’s symbols of first kind 176 179—182
Riemann’s symbols of second kind 175 177 178
Riemann’s symbols, Bianchi’s identities in 182
Rigid motion in any manifold 408
Roemer 307
Roemerian units 307
Rotation, Ricci’s coefficients of 268
Rotor of vector 161
Saturation (of indices) see “Contraction”
Sbrana 414
Scalar product of vectors 98 126 152
Schouten 172 198 231
schur 235
Schur’s Theorem 235
Schwarzschild 423
Schwarzschild’s solution of gravitational equations 419—423
Schwarzschild’s solution, extensions of 439
Second covariant derivatives 184
Second differential parameter 154 393
Second fundamental form of  252 252
Section of 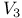 201 201
Section of manifold 163
Sereni 383
Sets of orthogonal directions 205
Sets of simple systems 74 156
Sets, reciprocal 74
Seven 22 171 196
Severi’s theorem 171
Shift, spectral 400
Signals, light, and coefficients of 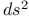 364—366 364—366
Simultaneity 290 311
Sirius, spectrum of Companion of 402
Sobral expedition 407
Solution of differential equations 36
Solution of gravitational equations, Schwarzschild’s 419—423
Solution of gravitational first approximation deduced from 425
Solutions, rigorous, of gravitational equations 437
Space of constant curvature, extension of 426 427 428
Space of constant curvature, gravitational equations in 428
Space, metric of, and Newtonian potential 391
Space, non-Euclidean 391
Space-time 290
Space-time metric, and energy tensor 374
Space-time with assigned Newtonian field 392
Space-time, an Einsteinian, ds’2 for 392
Space-time, co-ordinate transformations 290
Space-time, De Sitter’s 429—435
Space-time, De Sitter’s, constant negative curvature of 436
Space-time, Einstein’s and De Sitter’s, case including 435
Space-time, Einstein’s cylindrical 429
Space-time, Einstein’s, curvature of space in 438
Spatially uniform metrics 425
Spectral displacement 400
Sphere, geodesic, in 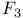 409 410 409 410
Spherical symmetry and gravitational equations 419
Spherical symmetry, metrics with 408—414
St. John 402
Statical 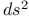 326 327 371 377 378 392 326 327 371 377 378 392
Statical field 400
Statical metrics 326 327
Stationary metrics 326 327
Stationary metrics, Fermat’s principle for 340
Stress 344
Stress and bilinear form 345
Stress in spatially symmetrical metrics 425 429 430 436 437 438
Stress tensor and equations of motion 351
Stress tensor in classical theory 344
Stress tensor in generalized co-ordinates 346
Stress tensor, divergence of 344 346 354
Stress tensor, interpretation of divergence 346
Stress, force absorbed in 349
Stress, kinetic 351 356 358
Stress, normal 345
Struik 231
| Sum of tensors 76
Surface vectors 96
Surface, geodesic 164
Surface, intrinsic geometry of 99
Surface, parametric equations of 86
Surfaces, developable 100
Symmetrical double systems 72
Symmetrical systems (tensors) 65
Symmetry, spherical, and gravitational equations 419
Symmetry, spherical, metrics with 408—414
System, mixed 70 71
Systems (tensors) of order m 65
Systems (tensors) of order zero 65
Systems (tensors), antisymmetrical 73
Systems (tensors), double 65
Systems (tensors), m-fold 65
Systems (tensors), symmetrical 65
Tensor 70 71
Tensor with vanishing elements 71
Tensor, Einstein’s 200 371
Tensor, energy 355
Tensor, energy, and equations of motion 359
Tensor, first general definition of 80
Tensor, gravitational 371
Tensor, gravitational, 10 components of 372
Tensor, Riemannian 371 (see also “Riemann’s symbols”)
Tensor, second general definition of 83
Tensor, stress, divergence of 344 346 354
Tensors, addition of 75
Tensors, associated 95 96
Tensors, composition of 79
Tensors, contraction of 77—79
Tensors, inner multiplication of 79
Tensors, multiplication of 76
Tensors, reciprocal 95
Third fundamental form of  259 259
Tietze 188
Time, conventional 364
Time, local 290 311 312
Total differential 13
Total differential, equations 13—33
Total differential, equations, complete svstem of 15—18
Trajectories 403
Trajectories and geodesies 324 326
Trajectories and light rays 343
Trajectories in generalized mechanics 324
Trajectories, Einsteinian and Newtonian 395
Trajectories, orthogonal 263
Transformation by contravariance 67 69—71
Transformation by covariance 64 67—71
Transformation by invariance 62
Transformation of derivatives 85
Transformation, affine 304 305
Transformation, formulae of 80
Transformation, homographic 304
Transformation, linear, of differentials 80
Transformations, linear 67
Transformations, Lorentz 300 308 310 316
Transformations, reversible 3 7 61
Transformations, space-time co-ordinate 290
Translation, motion of 305
Trefftz 439
Universe, radius of 439
Vanderlinden 439
Variations, Poincare’s equation of 208
Variety see “Manifold”
Vector, contravariant and covariant components of 97
Vector, contravariant, in  120 127 120 127
Vector, derivative of 139 140
Vector, determination of, by invariants 266
Vector, product 159
Vector, product of versors 201
Vector, projection of, in  127 127
Vector, transformation of 62 63 64
Vectors, equipollence of 103
Vectors, parallel and equal 103
Vectors, scalar product of 98 126
Vectors, surface or tangential 96
Vectors, zero 97
Velocities, absolute and relative 316—319
Velocities, composition of 306
Velocities, composition, according to Einstein 317
Velocity of light 292 306 311 334 335 339 382
Velocity of light, irreversible 340
Velocity of light, law of variation of 339
Velocity of light, non-symmetrical 340
Velocity, earth’s orbital 399
Velocity, large universal constant 291 292 311
Velocity, mass and 295
Versor (unit vector, direction) 92 96 98 102 103 123 125 126 140
Versor (unit vector, direction), in 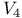 , and corresponding vector 329 , and corresponding vector 329
Versors and pseudo-Euclidean metrics 329
Versors, spacelike 330
Versors, timelike 330
Vibration of atom 400
Volume of curved space 427 428
Weber 14
Weyl 117 439
Whittaker 324
World lines 290 329 352 353
World lines of light 337 364
World lines, parameters and stress tensor 353
World lines, parameters of 353
Zeeman 319
Zero vectors 97
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте