|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Levi-Civita T. — The Absolute Differential Calculus (Calculus of Tensors) |
|
|
 |
| Предметный указатель |
Fresnel’s convection coefficient 319
Fresnel’s formula for velocity of light in moving media 318—320
Function, alternate 35
Function, implicit 3
Function, uniform 14
Functional matrix, characteristic of 9 39 87 250
Functions of position 80 83
G, linear invariant of Einstein tensor 380 381
Galilean systems 349
Galilean systems, force, stress and divergence in 349
Gauss 99 100 414
Gauss, on intrinsic geometry 99
Gaussian curvature 172
Gaussian curvature of 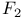 193 193
General relativity, concept of 294
General relativity, postulates of 364
Generalization of Lagrangian function 322—324
Generalization of metric of 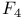 320 320
Geodesic curvature 135—137
Geodesic deviation 208—220
Geodesic deviation, Jacobi’s formula for 219
Geodesic excess 197
Geodesic manifold 162
Geodesic principle 337
Geodesic principle in 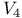 341 341
Geodesic principle, Einstein’s 328 331
Geodesic sphere as horizon 434
Geodesic surface 164
Geodesic triangle 197
Geodesic, co-ordinates locally 164 167 171
Geodesic, definition of 103 128
Geodesic, motion of particle in 326
Geodesies and trajectories 324 326 331
Geodesies autoparallelism of 104 140
Geodesies differential equations of 131—135
Geodesies in rigid motions 408
Geodesies in space of constant curvature 428
Geodesies Lagrange’s equations for 208 331 332 341 367 413
Geodesies near given geodesic 208
Geodesies of zero length 330—334 337
Geometrical optics 334
Geometrical optics according to Einstein 335—338
Goursat 14
Gravitation with point mass 419—423
Gravitation, modification of Newton’s law of 397
Gravitation, not absorbed in energy tensor 375
Gravitational constant 386
Gravitational equations and the facts 387
Gravitational equations for spherical symmetry 419
Gravitational equations for statical 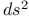 381 381
Gravitational equations in space of constant curvature 428
Gravitational equations, Einstein’s 376
Gravitational equations, modified by cosmological term 438
Gravitational equations, rigorous solutions of 437
Gravitational equations, solution of 419—423
Gravitational experiments and 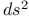 367 367
Gravitational field and spectral lines 400—402
Gravitational field, path of light in 403—408
Gravitational forces, as privileged 374
Gravitational tensor 371 372
Gravitational tensor, divergence of 372
Hamilton 287 288 291 293 294 296 298 301 320 322 351 385
Hamilton’s principle 287
Hamilton’s principle, Einstein’s form of 291
Hamilton’s principle, modified 294—298 301 322—324 351
Hessenberg 146
Hoelder 160
Horizon, in De Sitter’s space-time 434
Hyperspherical representation 258
Hypersurface 121
Hypersurface, hyperspherical representation of 258
Hypersurfaces in Euclidean space 249 253
Hypersurfaces, parallel 251
Immersion of  in Euclidean space 121 in Euclidean space 121
Indefinite 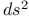 141 141
Independence of functions 5 8—10
Inertia, index of 299
Inertia, principle of, in relativity 298
Inner multiplication of tensors 79
Integral of differential equations 36 37
Integral, general 40 42 43 45 50
Integral, independent 40 42
Integral, principal 38 39 49
Intrinsic geometry of surface 99
Invariance and Hamilton’s principle 291
Invariance in relativity 322
Invariance of 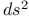 308 311 308 311
Invariance, m-fold system 69
Invariance, simple system 67
Invariance, transformation by 62
Invariant, derivatives of 83
Invariant, quadratic form 73 84
Isotropic manifolds 232
jacobi 209 219 220
Jacobi on geodesies 208
Jacobian systems of equations 52 53
Jacobians 2 (see also “Determinant Junctional”)
Jeans 383
Kasner 439
Kepler 377
Kinematics of modified 303
Kinematics of rigid systems 301
Kinematics, Galilean 318
Kinematics, relativity 311 316
Kummer 286
Kummer on congruences 286
Lagrange 289 295 413
Lagrange and geodesies 208 331 332 341 367 413
Lagrangian binomials 289
Lagrangian equations 289 331 332 341 367 413
Lagrangian parameters 288
Lamb 397
Laplace 394
Laplace’s operator 394
Laue 439
Law of gravitation, modifications of 397
Levi-Civita 104 139 172 272 286 324 334 381 383 394 397 398 429 439
Light in gravitational field, frequency of 400—402
Light, constancy of velocity of 335
Light, path in gravitational field 403—408
Light, path of, as trajectory 403
Light, propagation of, reversible 365
Light, rays and trajectories 343
Light, signals 364
Lipka 136 159
Local time 290 311 312
Longo 439
Lorentz 300 301 306 310 311 312 313 315 316 318 352 353 354
Lorentz transformation 300 308 310 316
Lorentz transformation, invariance for 352 353 354
Lorentz transformation, most general 313
Lorentz translation 316
Love 344
Maclaurin 166
Majorana 335
Manifold 1
Manifold, Euclidean 121
Manifold, geodesic 162
Manifold, metric 119
Manifold, n-dimensional 119
Manifold, sections of 162
Manifolds of constant curvature 236 238 240 246
Manifolds of constant, their mutual applicability 249
Manifolds, isotropic 232
Marcolongo 300 308
Mass and energy 294 298
Mass and metric of 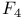 328 328
Mass and velocity 295
Matrices, functional 8—12
Matter, mean cosmic density of 439
| Matter, total quantity of 427 428
Mattioli 350
Maximum and minimum 128
Maxwell 383
Maxwell’s theory 383
Mayer 22 25 106
Mayer’s method of integration 25
Mechanical equivalence, a theorem of 394
Mechanics in covariant equations 348 349
Mechanics of continuous systems 347 352
Mechanics with any co-ordinates 347
Mechanics, classical, correction to 291—294 320 392
Mechanics, generalized 320—324
Metric of 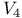 and physical phenomena 374 and physical phenomena 374
Metric of space-time and energy tensor 383
Metric of, generalization of 320
Metric, angular 123
Metric, pseudo-Euclidean 299 360
Metrical elements of figure 100
Metrics in conformal representation 229
Metrics with spherical symmetry 408—414
Metrics, different, covariant derivatives for 222
Metrics, different, for same  220 220
Metrics, different, Riemann’s symbols for 224
Metrics, relativity, qualities of 325
Metrics, relativity, statical 326
Metrics, relativity, stationary 326
Metrics, spatially uniform 425
Michelson 306 319 335
Michelson — Morley experiment 335
Minimum time, principle of 341 (see “Fermat’s Principle”)
Mixed system, or tensor 70 71
Mixed systems of total differential equations 29—33
Molecular action, system with no 360—363
Moments of co-ordinate lines 98
Moments of direction 92 120
Moments of direction, covariance of 92 120
Moments of direction, relation connecting 92 120
Momentum 295
Morera 22 25
Morera’s method of integration 22—25
Morley 306 319 335
Motion, Einsteinian, of planets 396
Multilinear form 66 69 83
Multiplication of tensors 76
Munari 316
Myller 106
Nebulae, density of 439
Newton 375 377 397
Newtonian equations 287 377
Newtonian field, assigned, space-time for 388—392
Newtonian motion, differences from Einsteinian 377
Newtonian potential 375
Newtonian potential and 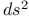 336 369 336 369
Normal congruence 263 275 277 285
normal form of differential equations 36
Nuyens 439
Operator  , properties of 176 , properties of 176
Operator, linear 33—37 48 84
Optics, geometrical 334
Orbit, equation of 397
Orthogonal directions, sets of 205
Padova 182
Palatini 146 408 439
Parallel displacement 103
Parallel displacement along a geodesic 103 104
Parallel displacement, angles unchanged by 103 114
Parallel displacement, cyclic 173 186
Parallel displacement, cyclic, of vector 192
Parallel displacement, cyclic, Peres’s formula for 193
Parallel, ambiental 171
Parallelism 102
Parallelism and curvature 193—198
Parallelism and infinitesimal displacement 104
Parallelism with respect to surface 102
Parallelism, Angle of 198
Parallelism, differential definition of 105
Parallelism, equations of 110—112
Parallelism, extension of notion of 137
Parallelism, intrinsic character of 106
Parallelism, intrinsic equations of 107
Parallelism, invariance of 110
Parallelism, symbolic equation of 107
Parallelogram rule for vectors 117
Parallels, kinematical construction of 102 104
Parameter of family of surfaces 45
Parameter, first differential 231 418
Parameter, second differential 154 393 418
Parameters and moments, relation of 92 125
Parameters of co-ordinate lines 98
Parameters of direction 91 120
Parameters of direction, contravariance of 91 120
Parameters of direction, relation connecting 91 120
Parameters, Lagrangian 288
Parametric equations of surface 86
Path of light, in gravitational field 402 403—408
Peres 172 193
Peres’s formula 193
Perihelion, displacement of 396 398
Perihelion, displacement of Mercury 399
Perihelion, displacement of other planets 400
Perihelion, displacement of, formula for 398
Permutability  116 116
Perot 402
Persico 102
Perturbations, Newtonian 399
Pfaff 14
Pfaffian 13 20 26 161 174
Pfaffian as invariant 81 82
Pfaffian systems 14
Physical phenomena and metric of 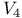 374 374
Planet, motion of 369
Planets, Einsteinian motion of 396
Planets, motion of, discrepancies in 322
Pluecker 68
poisson 35 53 56 375 376 377 386 387
Poisson’s equation and Einstein’s theory 386 387
Poisson’s equation for potential 375 377
Poisson’s parentheses 35 36
Postulates of general relativity 364
Potential and 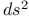 336 369 336 369
Potential and metric of space 391
Potential, Newtonian 287 292 297 322 323 369 375 377 388 394 396 400 403
Potentials, 10 gravitational 375
Principe expedition 407
Product of tensors 76
Pseudo-Euclidean 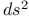 325 376 325 376
Pseudo-Euclidean every metric locally 360
Pseudo-Euclidean metric 299 360 383
Pseudo-Euclidean metric and versors 329
Quadratic differential form, invariant 84
Quadratic form 66
Quadratic form with non-vanishing discriminant 90
Quadratic form, 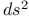 , character of 120 (see also “ , character of 120 (see also “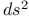 ”) ”)
Quadratic form, covariance of coefficients of 73
Quadratic form, definite 90
Quadratic form, invariant 73
Quadratic forms of class i 253
Quadratic forms of class zero 242
Quadratic forms, Euclidean 242
Quadratic forms, Riemann’s symbols for 242—246
Quadratic forms, theory of 205
Quadratic, canonical form of 205 281
Radioactivity 297
Radius of universe 439
Reciprocal elements in determinants 54 55 80 81
Reciprocal tensors 95
Refracting medium, space as 402
Refraction of light 334
Refractive index 334
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



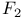
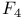
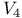
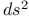
 in Euclidean space
in Euclidean space  , properties of
, properties of 