|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hartman P. — Ordinary Differential Equations |
|
|
 |
| Предметный указатель |
(u, v)-subset 281 291 293
Adjoint, dth order equation 66
Adjoint, dth order equation, linear system 62
Adjoint, dth order equation, system of total differential equations 119 (see also “Associate operator”)
Admissible 438 462 481
Angular distance 451
Arzela theorems 4
Ascoli theorems 4
Associate operator 486
Asymptotic integration, boundary layer theory 534
Asymptotic integration, boundary layer theory, difference equation 241(Ex. 5.4) 289(Ex. 290(Ex.
Asymptotic integration, boundary layer theory, dth order equation 314 447(Ex.9.2(c))
Asymptotic integration, boundary layer theory, perturbed linear system 212 259 273 445 447(Ex.
Asymptotic integration, boundary layer theory, second order equation 319(Ex. 17.4 17.5) 320(Ex. 369 375 446 447(Ex.
Asymptotic lines 107(Ex. 6.3(c))
Asymptotic phase 254
Asymptotic stability see “Stability”
Attractor 160 213
Attractor, domain of attraction 548
Autonomous system 38 144 202
Banach spaces, admissible 438 462 481
Banach spaces, admissible,  , , 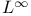 , , 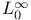 , M 436 453 , M 436 453
Banach spaces, admissible, associate 484
Banach spaces, admissible, class 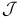 , , 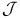 452 484 452 484
Banach spaces, admissible, lean at  439 439
Banach spaces, admissible, open mapping theorem 405 437 439 464
Banach spaces, admissible, quasi-full 453 467 471 474 475
Banach spaces, admissible, Schauder fixed point theorem 405 414 425
Banach spaces, admissible, stronger than L 437 453
Bessel equation 87(Ex. 12.3(a))
Bessel equation, 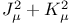 518(Ex. 4.2). 519(Ex. 4.3) 518(Ex. 4.2). 519(Ex. 4.3)
Bessel equation, asymptotic behavior of solutions 371 (Ex. 8.1)
Bessel equation, integral of 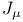 513 (Ex. 3.6) 513 (Ex. 3.6)
Bessel equation, zeros of solutions 336(Ex. 3.2(d)) 519(Ex.
Blasius differential equation 520
Bohl theorem 199
Boundary layer theory 519
Boundary value problems 337 407 418 519
Boundary value problems, adjoint 410
Boundary value problems, linear, first order 407
Boundary value problems, linear, second order 418
Boundary value problems, nonlinear, second order 422 433 434(Ex.
Boundary value problems, periodic, nonlinear 412 435(Ex.5.9(6))
Boundary value problems, singular, third order 519
Boundary value problems, Sturm — Liouville 337
Bounds for solutions 30
Bounds for solutions, autonomous system 543
Bounds for solutions, derivatives 428
Bounds for solutions, equation of variation 110
Bounds for solutions, second order equation 373(Ex. 8.6) 374(Ex.
Brouwer fixed point theorem 278
Cantor selection theorem 3
Cauchy, characteristic strips 133 135
Cauchy, characteristic strips, initial value problem 131 137 140
Center 159 215 216(Ex.
Characteristic direction 209 220
Characteristic equation (polynomial) 65
Characteristic roots and exponents 61 252 253
Characteristic strips 133 135
Comparison theorem, principal solutions 358
Comparison theorem, principal solutions, second order equations 333
Comparison theorem, principal solutions, second order systems 391(Ex. 10.2)
Comparison theorem, principal solutions, Sturm 333
Complete integrability 118 123 128
Complete Riemann metric 541 546
Complete system of linear partial differential equations 119 120(Ex. 124
Conjugate, points (Jacobi’s theorem) 391(Ex. 10.1)
Conjugate, points (Jacobi’s theorem), solutions 385 386 399
Constant coefficients, dth order equation 65
Constant coefficients, dth order equation, linear system 57
Constant coefficients, dth order equation, second order equation 324 (Ex. 1.1)
Continuum 16
Curvature, quadratic form 106(Ex. 6.2 63(b))
Curvature, quadratic form, lines of 107(Ex. 63(d))
Curvature, quadratic form, Riemann tensor 106(Ex. 6.2)
Cycles see “Limit cycles”
Derivate 26
Dichotomies, adjoint systems 484
Dichotomies, adjoint systems, definitions 453
Dichotomies, adjoint systems, first order systems 474
Dichotomies, adjoint systems, Green’s functions 461 476 477
Dichotomies, adjoint systems, higher order systems 478
Dichotomies, adjoint systems, second order equations 483(Ex. 7.1) 496(Ex. 13.2)
Difference equations 241 (Ex. 5.4) 289 290(Ex.
Differential forms 101 120
Differential inequalities 24
Differential inequalities, equations of variation 110
Differential inequalities, linear systems 54
Differential inequalities, partial 140 141 142(Ex.
Disconjugate equation of second order 351 362
Disconjugate equation of second order, positive solutions 351 352(Ex.
Disconjugate equation of second order, variational principles 352 (see also “Nonoscillatory”)
Disconjugate system of second order 384
Disconjugate system of second order, criterion 388 390 391 10.2) 420 421(Ex.
Domain of attraction 548
Egress point 37 175 202 278 281 520
Eigenfunction 338 342
Eigenfunction,  -approximation (completeness) 338 -approximation (completeness) 338
Eigenfunction, interpolation 344(Ex. 4.4)
Equations of variation 96 110
Equations of variation, bounds for solutions 110
Equicontinuity 3
Equivalence, differential equations 258 271(Ex.
Equivalence, differential equations, maps 258
Ergodic 193 194 198 199
Euler differential equation 85
Existence in large 29
Existence in large for linear systems 31 45
Existence theorems, boundary value problems 337 407 418 519
Existence theorems, boundary value problems, Cauchy problem 137
Existence theorems, boundary value problems, invariant manifolds 234 242 296
Existence theorems, boundary value problems, linear system of partial differential equations 124
Existence theorems, boundary value problems, maximal solution 25
Existence theorems, boundary value problems, monotone solution 357 506 514
Existence theorems, boundary value problems, PD-solution 497
Existence theorems, boundary value problems, Peano 10
Existence theorems, boundary value problems, Picard — Lindelof 8 (see also “Periodic solution” “Solutions
Extension theorem 12
Exterior, derivatives 102
Exterior, derivatives, forms 101 120
Fixed point theorems see “Brouwer” “Schauder” “Tychonov”
Floquet theory 60 66 71 302(Ex.
Focus 160 215 216(Ex.
Formal power series 78 79 261
Frechet space 405 436
Frobenius, factorization 67
Fuchs, theorem 85
Fuchs, theorem, type of differential equation 86(Ex. 12.2)
Fundamental matrix or solution 47
Fundamental matrix or solution, adjoint system 62
Fundamental matrix or solution, analytic system 70
Fundamental matrix or solution, characteristic exponents and roots 61
Fundamental matrix or solution, Floquet theory 60 71 302(Ex.
Fundamental matrix or solution, system with constant coefficients 57
Fundamental matrix or solution, unitary 62(Ex. 7.1)
Geodesies 106(Ex. 6.2)
Global asymptotic stability 537
Green’s formula 62 67 327 385
Green’s functions 328 328(Ex. 2.2) 338 409(Ex. 439 441 461 476 477
Gronwall inequality 24
Gronwall inequality, generalized 29
Gronwall inequality, systems 29 (Ex. 4.6)
Haar’s lemma 139
Half-trajectory 202
Hermitian part of a matrix 55 420
Homann differential equation 520
Hypergeometric equation 509 (Ex. 2.6(b))
Hypergeometric equation, Kummer’s confluent form 509 (Ex. 2.6(c))
Implicit function theorem 5 11
INDEX see “Jordan curve” “Stationary
| Indicial equation 85
Inhomogeneous equations see “Variation of constants”
Integrability conditions 118 119 123 128
Integral, first 114 124
Integral, first, (m+1)st 478
Invariant manifold 228 234 242 296
Invariant set 184 184(Ex. 11.3)
Jacobi, system of partial differential equations 120
Jacobi, theorem on conjugate points 391 (Ex. 10.1)
Jordan curve, flow on 190
Jordan curve, flow on, index and vector field 149 173
Jordan curve, flow on, theorem 146
Jordan normal form 58 68
Kamke uniqueness theorem 31
Kneser, H., theorem 15
Kronecker theorem 194
Lagrange identity 62 67 327
Legendre equation 87(Ex. 12.3(6))
Legendre equation, associated equation 87(Ex. 12.3(c)) 508(Ex.
Lettenmeyer theorem 87 91
Lienard equation 179
Limit cycle 145 151 152 156 178 181 10.5) 190 253
Limit points, 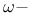 and and 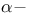 145 184 145 184
Limit points, 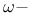 and and 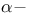 , set of , set of  -limit points 145 154 155 158 184(Ex. 11.4) 190 193 -limit points 145 154 155 158 184(Ex. 11.4) 190 193
Linearizations, differential equations 244 257(Ex. 258
Linearizations, differential equations, maps 194 245 257
Linearly independent solutions 46 64 326
Liouville, formula 46
Liouville, formula, Sturm — Liouville problems 337
Liouville, formula, substitution 331
Liouville, formula, volume preserving map 96(Ex. 3.1)
Lipschitz, continuity 3
Lipschitz, continuity, S- and L-Lipschitz continuity 107
Lyapunov, asymptotic stability 38 40 539
Lyapunov, asymptotic stability, function 38 40 539
Lyapunov, asymptotic stability, order number 56 294 301 303
Lyapunov, asymptotic stability, stability 38 40
Lyapunov, asymptotic stability, theorem on second order equation 346
Lyapunov, asymptotic stability, uniform stability 40
Manifold, definition of 2-manifold 182
Manifold, definition of 2-manifold, flow on 183
Manifold, definition of 2-manifold, invariant 228 234 242 296
Manifold, definition of 2-manifold, P(B, D)-manifold 484
Manifold, definition of 2-manifold, stable and unstable 238 244 255
Maps, associated with general solution 94 96 231
Maps, associated with general solution, associated with periodic solution 251
Maps, associated with general solution, equivalence 258
Maps, associated with general solution, invariant manifolds 234
Maps, associated with general solution, linearization 194 245 257
Maps, associated with general solution, volume preserving 96(Ex. 3.1)
Matrix, exponential of 57
Matrix, exponential of, factorization of analytic 75
Matrix, exponential of, Jordan normal form 58 68
Matrix, exponential of, logarithm of 61
Matrix, exponential of, norm 54
Matrix, exponential of, trace (tr) 46 (see also “Fundamental matrix”)
Maximal interval of existence 12
Maximal solution 25
Minimal set 184 184(Ex. 11.4) 185 190 193
Monotony 500
Monotony, functions of solutions 500 510 518 519(Ex.
Monotony, solutions 357 506
Nagumo theorems 32 428
Node 160 216 216(Ex. 3.3) 219
Nonoscillatory equations of second order 350 362
Nonoscillatory equations of second order, criteria 362
Nonoscillatory equations of second order, necessary conditions 367 368
Norm, matrix 54
Norm, matrix, on 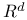 3 3
Open mapping theorem 405 437 439 464
Operator, associate 486
Operator, associate, closed 405
Operator, associate, graph 405
Operator, associate, null space 462
Order number 56 294 301 303
Oscillatory 333 351 369 510
Osgood uniqueness theorem 33
Peano, differentiation theorem 95
Peano, differentiation theorem, existence theorem 10
Periodic solution, associated map on transversal 251
Periodic solution, associated map on transversal, characteristic roots 61 252
Periodic solution, existence 151 178 179(Ex. 179 181 198 407 412 415 416 435(Ex.
Periodic solution, existence, Floquent theory 60 66 71 302(Ex. “Stability”)
Perron — Frobenius theorem 507(Ex. 2.2)
Perron — Frobenius theorem, total differential systems 117 120
Perron, singular differential equation 91(Ex. 13.1)
Perron, singular differential equation, theorem of Perron — Frobenius 507 (Ex. 2.2)
Perturbed linear systems 212 259 273
Perturbed linear systems, invariant manifolds 242 296
Perturbed linear systems, linearization 244 257(Ex.
Picard — Lindelof theorem 8
Poincare — Bendixson theorem 151
Poincare — Bendixson theorem, generalized 185
Polya’s mean value theorem 67 (Ex. 8.3)
Principal solution of second order equation 350 355
Principal solution of second order equation, comparison 358
Principal solution of second order equation, continuity 360
Principal solution of second order equation, definition and existence 355 357
Principal solution of second order equation, monotone 357
Principal solution of second order system 392 398
Prufer transformation 332
Quasi-full Banach space 453 467 471 474 475
Reduction of order 49
Reduction of order, second order equation 64 327
Regular growth 514(Ex. 3.7)
retract 278
Retract, quasi-isotopic deformation 280(Ex. 2.1)
Riccati, equations 331 364
Riccati, equations, differential inequality 362 364 368
Riccati, equations, generalized equation 226(Ex. 4.6)
Riesz, F,. theorem 387
Rotation number 191 198
Rotation point 158 173(Ex.
Saddle-point 161 216 218
Sauvage theorem 73
Sauvage theorem, partial converse 74
Schauder fixed point theorem 405 414 425
Schwartz, A. J., theorem 185
Second order, linear equation 322
Second order, linear equation, linear system 384 418
Second order, linear equation, nonlinear 174 422 “Boundary “Bounds” “Comparison “Dichotomies” “Disconjugate” “Liouville” “Monotony” “Nonoscillatory” “Principal “Prufer” “Riccati” “Solutions “Sturm” “Variation “Zeros”)
Sectors (elliptic, parabolic, hyperbolic) 161
Sectors (elliptic, parabolic, hyperbolic), index of stationary point 166
Sectors (elliptic, parabolic, hyperbolic), level curves 173 (Ex. 9.1)
Self-adjoint, operator 342
Self-adjoint, operator, dth order equation 398
Singular point, simple 73 78(Ex. 84 86(Ex.
Singular point, simple, regular 73 78(Ex. 85 86
Small at  486 486
Solution, definition 1 46(Ex.
Solution, definition, continuity with respect to initial conditions or parameters 94
Solution, definition, D-solution 437
Solution, definition, differentiability with respect to initial conditions or parameters 95 100 104 115
Solution, definition, PD-solution 462
Solutions tending to 0, binary systems 161 208 209 211 220
Solutions tending to 0, binary systems, linear system’s 500
Solutions tending to 0, binary systems, perturbed linear systems 259 294 300 304 445
Solutions tending to 0, binary systems, second order equations 510 514 (Ex.
spirals 151 159 190 211 216 220
Square root, differential operators 354 392
Square root, non-negative Hermitian matrix 503(Ex. 1.2)
Stability, asymptotic 38 40 537
Stability, asymptotic, global 537
Stability, asymptotic, Lyapunov 38 40
Stability, asymptotic, orbital 157 254
Stability, asymptotic, periodic solutions 158 178 179 253 302(Ex.
Stability, asymptotic, uniform 40
Stationary point 144 183 209 212 220
Stationary point, index 149 166 173 “Focus” “Node” “Saddle-point”)
Sturm, comparison theorems 333 362
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
, 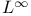 ,
, 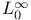 , M
, M 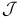 ,
, 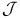

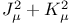
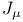
 -approximation (completeness)
-approximation (completeness) 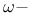 and
and