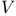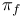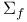|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Borceux F. — Handbook of Categorical Algebra 3 |
|
|
 |
| Предметный указатель |
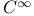 -algebra II.136 -algebra II.136
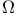 -set 144 -set 144
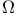 -set, complete 156 -set, complete 156
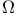 -set, epimorphism of 148 -set, epimorphism of 148
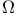 -set, monomorphism of 150 -set, monomorphism of 150
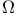 -set, morphism of 145 -set, morphism of 145
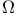 -set, singleton of a 157 -set, singleton of a 157
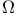 -subset 152 -subset 152
Abelian II.13
Addition 468
Adjoint arrows I.284 I.305
Adjoint functor theorem I.109
Adjoint functor theorem, special I.110
Adjoint functor theorem, the more general I.277
Adjoint functors I.98
Adjoint functors, fibred II.394
Adjoint lifting theorem II.230
Adjunction I.98
Algebra II.189
Algebra, free II.191
Algebra, morphism II.189
Algebraic theory II.130
Algebraic theory, commutative II.166
Algebraic theory, morphisrn of II.143
Algebraic theory, presentation of an II.125 II.133
Algebraic theory, tensor product of II.174 II.176
arrow I.4
Arrow, codomain of an I.5
Arrow, domain of an I.5
Arrow, identity I.4
Arrow, source of an I.5
Arrow, target of an I.5
Associated sheaf functor 121 497
Asterisk II.359
Axiom II.123 II.125 II.2
Axiom of Choice 447
Axiom of extensionality 410
Axiom of replacement 411
Axiom, power set 416
Banach spaces II.257
Beck condition 316 341
Bicategory I.302
Bifunctor I.23
Bihomomorphism II.167
Bilimit I.295
Bimodule I.307 I.308
Biproduct II.5
Boolean algebra II.135 II.9
Calculus of fractions I.183
Cardinal I.268
Cardinal, finite 481
Cardinal, regular I.268
Cartesian closed category II.294
Cartesian functor II.382
Cartesian morphism II.375
Cartesian natural transformation II.382
Category I.4 370
Category of arrows over 7 I.7
Category of arrows under I I.7
Category of elements I.22
Category of fractions I.181
Category with absolute colimits I.272
Category with enough projectives I.164
Category,  -filtered I.268 -filtered I.268
Category, 2-category I.282
Category, 3-category I.292
Category, abelian II.13 II.109
Category, accessible II.263
Category, additive II.6
Category, algebraic II.158 II.257
Category, bicategory I.302
Category, cartesian closed I.335 II.349
Category, Cauchy complete I.274 II.266 II.289
Category, comma I.20 I.91
Category, complete I.59 I.107
Category, connected I.58
Category, cotensored II.320
Category, discrete I.7
Category, dual I.33
Category, enriched 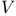 II.300 see II.300 see
Category, exact II.105 II.109
Category, fibred II.375
Category, fibred comma II.434
Category, filtered I.76 371
Category, finitely complete I.59
Category, finitely generated I.63
Category, finitely well-complete I.147
Category, locally cartesian closed I.339
Category, locally presentable I.241 II.256
Category, Mal’cev II.121
Category, monoidal II.291
Category, n-category I.293
Category, preadditive II.4
Category, regular I.236 II.90 II.92 II.93
Category, small I.6
Category, symmetric monoidal closed II.167
Category, tensored II.320
Category, well-powered I.132
Cauchy completeness I.319
Cauchy completion I.277 II.289
cell I.283
Cell, 0-cell I.283
Cell, 1-cell I.283
Cell, 2-cell I.283
Cell, 3-cell I.292
class I.3
Class, colimit closed I.205
Class, saturated I.190
Closed subset 70
Closed subset, irreducible 70
CoCone I.57
Coend II.329
Coequalizer I.49
Coequalizer, split II.212
Cofibration II.382
Cogenerator I.167
Coherent theory 367
Coherent theory, model of a 368
Coherent theory, morphism of models of a 368
Cokernel II.2
Colimit I.57
Colimit,  -filtered I.268 -filtered I.268
Colimit, absolute I.66
Colimit, filtered I.76
Colimit, universal I.85
Colimit, weighted II.327
Commutative diagram I.5
Commutativity condition I.177
Comonad II.219
Compact element II.141 74
Compact space II.236
Compactly continuous II.360
Compatible family 88
Complemented element 436
Comprehension scheme 414
Cone I.56
Cone, lax-cone I.300
Cone, pseudo-cone I.300
Congruence II.139
Constant II.122 346
Continuous mapping 16
Continuous mapping, open 44
Coproduct I.44
Coproduct in a fibration II.412
Coproduct, associativity of I.45
Coproduct, disjoint 216
Coreflection along a functor I.98
Cotensor II.320 II.331
Covering 373
Crossed module I.339
| de Morgan’s laws 9
Decidable object 444
Deduction rule 2
Definable class II.424
Definable class of arrows II.424
Definable class of diagrams II.431
Definable class of objects II.424
Definable subfibration II.424
Descent data II.240
Descent morphism II.253
Descent morphism, effective II.242
Descent theory II.237
Diaconescu theorem 280
distributor I.308
Division 477
Double Negation 8 510
Duality principle I.33
Eilenberg — Moore category II.189
Element 373
Embedding theorem II.112
END II.329
Enriched II.300
Enriched adjunction II.340
Enriched category II.300
Enriched distributor II.306
Enriched functor II.301
Enriched Kan extension II.344
Enriched natural transformation II.301
Enriched Yoneda embedding II.313
Enriched Yoneda lemma II.311
Epimorphism I.27
Epimorphism, extremal I.136
Epimorphism, regular I.136
Epimorphism, strong I.137 I.197
Epimorphism, universal II.120
Equality 304
Equalizer I.48
EQUIVALENCE I.284
Equivalence of categories I.116
Etale mapping 108
Exact sequence II.32 II.33 II.95
Exact sequence, short II.34 II.87
Excluded Middle 432
Factorization I.148
Factorization system I.209
Factorization, epi-strong-mono I.149
Factorization, strong-epi-mono I.148
Faithful embedding theorem II.73
FALSE 344
Fibration II.375
Fibration, cocomplete II.412
Fibration, complete II.402
Fibration, dual II.393
Fibration, finitely complete II.402
Fibration, internally complete II.402
Fibration, localized II.402
Fibration, locally small II.412
Fibration, power II.398
Fibration, small II.379
Fibration, split II.392
Fibre II.374
Fibred adjunction II.394
Fibred internal limit II.402
Fibred limit II.401
Field II.182 370
Filter 62
Filter, completely prime 62
Filter, prime 62
Final object I.48
Finite object 480 481
Five lemma II.41
Fixed element 299
Formula 346
Formula, coherent 363 367
Formula, valid 358
Free Abelian group I.102
Free group I.102
Free monoid I.102
Free ring I.103
Frobenius identity 38
Fubini formula II.347
Full and faithful embedding theorem II.80
functor I.5
Functor 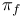 327 327
Functor 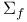 327 327
Functor preserving monomorphisms I.24
Functor reflecting monomorphisms I.24
Functor with rank II.272
Functor,  -flat I.270 -flat I.270
Functor, 2-functor I.287
Functor, absolutely flat I.271
Functor, additive II.8
Functor, additive representable II.12
Functor, algebraic II.145
Functor, cartesian II.382
Functor, collectively faithful family I.154
Functor, contravariant I.16
Functor, cotopological II.368
Functor, covariant I.16
Functor, dominated II.183
Functor, exact II.50 II.97
Functor, faithful I.19
Functor, family of functors collectively reflecting isomorphisms I.154
Functor, fibre small II.370
Functor, final I.69
Functor, flat I.260 II.274
Functor, forgetful I.8
Functor, full I.19
Functor, full and faithful I.19
Functor, hom-functor I.34
Functor, identity I.6
Functor, inverse image II.393
Functor, lax-functor I.296
Functor, left adjoint I.98
Functor, left exact I.250 II.50
Functor, limit preserving I.64
Functor, limit reflecting I.65
Functor, monadic II.212
Functor, pseudo-functor I.297
Functor, representable I.9
Functor, right adjoint I.98
Functor, right exact II.50
Functor, topological II.367
Functor, \alpha$-left-exact I.269
G-sets II.136 II.297 II.298
Galois connection I.105
Generator I.151
Generator, dense I.153
Generator, dense family of -s I.153
Generator, family I.151 138
Generator, strong family I.152 I.157
Generator, strong- I.152 I.157
Geometric morphism 183
Germ 113
Giraud theorem 230
Global element 291
Global support II.120
Graph I.176
Graph, conditional I.178
Graph, morphism I.176
Grothendieck topology 196
Group II.122
Group, torsion free II.232
Groupoid I.287
Hereditary covering 192
Hereditary subset 192
Heyting algebra II.300 5
Heyting algebra, complete 14
Hilbert spaces II.289
Homomorphism II.126 II.130
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



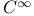 -algebra
-algebra 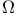 -set
-set  -filtered
-filtered